基于角域AR模型滤波的滚动轴承故障诊断*

程卫东， 刘东东， 赵德尊

(北京交通大学机械与电子控制工程学院 北京，100044)

引 言

变转速工况下滚动轴承的故障诊断需要消除转速变化对振动信号的影响[1]，消除转速变化常使用阶比跟踪技术，将时域信号转化为角域信号[2-3]。阶比跟踪过程中需要转速信息，有两种方式获得转速[4]：a.通过转速计等硬件设备直接测取；b.在振动信号中提取。由于在实际工况中受到安装成本以及安装空间的限制，从振动信号中提取转速引起了学者的广泛关注。文献[5]利用带通滤波获取转频特定的谐波成分后再进行相位解调对瞬时转频进行估计，该方法虽然有效，但仅适合转速在小范围内波动的工况。文献[6]使用短时傅里叶变换(short time Fourier transform, 简称STFT)变换与 Viterbi 拟合算法相结合估计变转速模式下的振动信号瞬时转频。文献[7]根据经STFT变换的时频分析结果，利用峰值搜索算法对变转速运行机械的瞬时转频进行估计。然而，在齿轮噪源影响下，轴承的转速分量相对较小，依靠上述算法在混合信号中提取转速信息很困难。

文献[8-9]提出以故障特征频率(fault characteristic frequency, 简称FCF)代替转频对振动信号进行角域重采样，这是因为FCF在时频域中表现出明显的峰值，提取FCF相对于转频容易。基于FCF角域重采样的原理是先对FCF趋势线积分，然后根据积分曲线求得转过等角度间隔时的时间点，从时域信号中获得各时间点的峰值。然而，基于FCF的阶比分析存在不足之处。首先，在信噪比比较低的情况下，作为参考量的较小转频分量会被噪声淹没，导致基于FCF的阶比分析不能确定故障发生的位置；其次，在齿轮噪声存在的情况下，这种方法可能会出现误判。

齿轮噪源干扰下轴承转频分量提取困难并且以FCF代替转频进行阶比分析具有不足之处，因此，有必要寻找一种新的易提取的频率成分来弥补以上不足。齿轮噪源干扰下的振动信号中虽然转频分量相对较小，但是齿轮啮合频率的幅值很大，并且啮合频率与转频存在倍数关系。因此，如果能从振动信号中提取齿轮的啮合频率便可以估计转频。近年来, 文献[10]提出了线调频小波路径追踪(chirplet path pursuit, 简称CPP)算法，可以提取复杂信号中的瞬时频率，并且已经开始应用于机械故障诊断中[11]。使用CPP算法可以从时域信号中提取峰值最大的瞬时频率趋势线，而齿轮瞬时啮合频率(gear instantaneous meshing frequency, 简称GIMF)在时域中具有高幅值的特点，所以，可以利用CPP算法从时域信号中提取GIMF趋势线。因此，可以直接在时域信号中提取GIMF趋势线，然后根据 GIMF与转频关系估计转频，利用估计转频对原信号进行等角度重采样，获得角域信号。

齿轮噪声的去除也是轴承故障诊断中非常棘手的问题。文献[12]指出周期与随机量分离算法要求保证轴承的转速不存在波动。张西宁等[13]运用同步平均的方法对信号进行处理，当轴承转速发生变化时，同步平均不能完全去除齿轮啮合、不对中产生的噪声成分。文献[14]利用AR模型去除恒转速下混合信号的可线性预测的周期平稳成分，但是AR模型对去除信号成分的周期性要求很严格，在变转速工况下，齿轮啮合频率及其谐波失去了周期性。AR模型对去除信号的周期性要求很严格，但是齿轮噪声成分在经过估计转频重采样的角域信号中恢复了其周期性，因此，可以使用AR模型去除角域信号中的齿轮噪声成分。

鉴于此，提出了不依靠转速计等辅助设备的基于角域AR模型滤波处理方法。首先，使用线调频小波路径追踪算法提取降采样处理的混合信号中GIMF趋势线并估计转速；其次，根据估计转速对原混合信号进行等角度重采样，并利用角域信号中齿轮啮合振动成分具有周期性的特点使用AR模型对其滤波；最后，对滤波后信号进行Hilbert变换和快速傅里叶变换(fast Fourier transform, 简称FFT)得到阶比谱，完成故障判断。

1 算法部分

1.1 线调频小波路径追踪算法

线调频小波路径追踪是利用一系列的瞬时频率为线性变化的chirplet原子，在整个时间长度上通过最佳路径连接的算法逐一连接，从而提取分析信号的瞬时频率。其具体算法如下。

建立chirplet原子库

hI(t)=|I|-1/2e-i(aμt2/2+bμt)LI(t)

(1)

其中：I为动态支撑区间，I=[kN2-j,(k+1)N2-j]×Δt；k为动态区间的序号，k=0,1,…,2j-1；N为分析信号的采样点数；j为动态支撑区间的尺度系数，j=0,1,…,log2N-5；LI(t)为矩形窗函数(即t∈I时，LI(t)=1；t∉I时，LI(t)=0)；aμ为调频率系数；bμ为频率偏置系数；aμt+bμ为动态支撑区间内瞬时频率，应小于fs/2。

定义分析信号为信号与所有原子的内积，即

(2)

其中：Δt为采样时间间隔；n为t时刻采样点数。

在原子库中寻找一组原子连接，使分析信号在时间支撑区域上有最大的投影系数。支撑区间内最大投影系数为

(3)

定义最大投影系数kI在时间支撑区I内代表的信号分量为dI(t)，得

dI(t)=|kI|e-i(at2/2+bt)LI(t)

(4)

连接最大投影系数kI，使得信号分量dI(t)信号具有最大的总能量，即

(5)

其中：Π应覆盖整个时间长度且不重叠。

由此获得最佳路径连接算法如下。

1) 初始化 取e(i)=0，pred(i)=0。其中：e(i)为i-1个动态时间支撑区的最大投影系数对应的总能量和；pred(i)为连接到第i个动态时间支撑区的前置支撑区的序号。

2) 对动态时间支撑区集合{Ii|i∈z}，找到与其相邻的下一个动态时间支撑区集合{Ik|k∈z}，若

e(i)+d(i)>e(k)

(6)

则令

(7)

该连接方法能确保基原函数的组合与分析信号的相似度最高，而动态支撑区Π内的瞬时频率为aμt+bμ(ti∈Ii)，线性连接各个支撑区的瞬时频率就获得了分析信号的瞬时频率。

1.2 基于GIMF趋势线的等角度重采样算法

利用CPP算法从振动信号中提取GIMF趋势线，根据GIMF与转速成齿数倍关系，可以估计出与齿轮同轴的轴承转频。基于GIMF趋势线的等角度重采样算法的具体算法如下。

1) 利用CPP算法提取GIMF趋势线，利用三次多项式对其进行拟合并估计转频

f(t)=at3+bt2+ct+d

(8)

fr(t)=f(t)/z=(at3+bt2+ct+d)/z

(9)

其中：f(t)为GIMF；fr(t)为估计转频；z为齿轮的齿数。

2) 确定阶比分析的最大阶次Dmax以及对应的等角度采样时的角增量Δθ

(10)

3) 计算等角度重采样的数据点数N

(11)

其中：T为信号采集时间；Δθ为角域采样间隔。

4) 计算等角度重采样的鉴相时标Tn

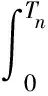
(12)

其中：T0为采样起点；n= 0,1,… ,N。

5) 以振动信号的时域采样点为基础，利用Lagrange线性插值定理计算鉴相时标Tn处对应的幅值以完成基于GIMF的等角度重采样算法

(ti≤Tn≤ti+1)

(13)

1.3 齿轮噪声消除的AR模型算法

线性预测是一种基于AR模型的预测方法，其自回归特性体现在当前的输出是当前的输入与过去的一部分输出的加权和，因此可以对信号进行预测。

设x是长度为N的零均值平稳信号序列，p为AR模型的阶数，则x的AR模型可以表示为

(14)

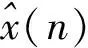
(15)

在线性预测过程中的一个关键问题是AR模型阶次p的选取，过高过或过低的模型阶数将直接影响到预测结果的效用。

在滚动轴承的故障诊断中，线性预测被用于剥离混合信号中的周期成分。因峭度指标对信号冲击成分的高度敏感性，这里使用基于峭度值最大的AR模型定阶准则

(16)

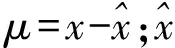
当残余信号的峭度值达到最大值时，返回的AR模型阶次k即为线性预测滤波器的最优阶次。

2 基于角域AR模型滤波的诊断方法

当滚动轴承出现凹坑或裂纹时，故障点与其接触点会产生冲击，由于系统的衰减特性，形成高幅值而快速衰减的冲击响应[15]。根据轴承结构的尺寸参数便可以得到故障特征系数(fault characteristic coefficient, 简称FCC)

其中：fo，fi和fb分别为外圈、内圈和滚动体的故障特征频率；fr为轴承转频；N为滚动体个数；d为滚动体直径；D为节圆直径；φ为接触角。

由式(17)，(18)和(19)可以看出，FCF与转频存在着固定的倍数关系，比值为FCC。因此，以轴承的转速为基准对信号进行等角度重采样，再做包络阶比谱分析，会在横坐标FCC以及倍数处出现峰值。然而，在齿轮噪源和变转速双重干扰下的振动信号中，轴承的转速分量相对较小，直接提取困难。相反，GIMF具有较大峰值，提取容易。GIMF与转速之间的关系为

fm=frz

(20)

其中：fm为齿轮啮合频率；fr为齿轮所在轴的转速；z为该齿轮的齿数。

由式(20)可以看出，齿轮的GIMF和与齿轮同轴的轴承转速成整齿数倍关系，通过提取GIMF趋势线，便可以估计此轴的转频。使用基于GIMF趋势线的等角度重采样算法对振动信号进行处理便获得角域信号。由于在角域信号中齿轮啮合频率及其谐波，属于确定性周期信号，因此，使用AR模型可以剥离振动信号中的GIMF。

鉴于此，提出了基于角域AR模型滤波的滚动轴承的故障处理方法如下：

1) 对混合信号进行降采样，使用CPP算法提取降采样处理的混合信号中的GIMF趋势线；

2) 分析轴承转速与齿轮GIMF的关系，根据GIMF趋势线估计转速曲线；

3) 根据估计转频对原混合信号进行等角度重采样，并使用AR模型对其滤波，获得去除齿轮噪声的滤波后信号；

4) 对滤波后信号进行Hilbert变换和FFT变换得到阶比谱，完成故障判断。

方法流程图如图1所示。

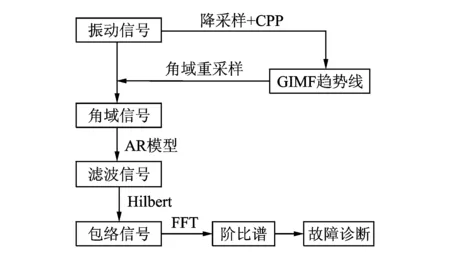
图1 基于角域AR模型的故障处理方法流程图Fig.1 Flow chart of bearing fault diagnosis based on AR model filtering in angle domain

3 仿真信号分析

为了验证笔者提出方法的有效性，对滚动轴承的仿真信号进行分析。模拟滚动轴承的外圈出现故障，故障特征系数C0=5，滚动轴承的转速如图2所示，随时间成线性变化

v(t)=10t+5

(21)

图2 仿真信号转频与伪IFCF趋势线Fig.2 Simulation signal rotating frequency and false IFCF

轴承转过角度与时间之间的关系为

(22)

其中：θi=i/C0(i=1,2,…,k)。

由以上两个公式可以求得每个冲击对应的时标Ti。该混合信号主要由故障轴承的冲击成分xbearing、齿轮啮合振动产生信号成分xgear和白噪声成分n(t)三部分构成，如式(23)所示

x(t)=xbearing+xgear+n(t)

(23)

笔者改进了匀转速工况下滚动轴承的振动信号的仿真模型[16]，构造转速变化工况下故障滚动轴承振动信号的仿真模型

(24)

其中：Ai为第i个冲击的幅值，简化该幅值与时间成线性关系；fr为共振频率；φω为初相角，设置为0；λ为滑移常数，参考轴承转速的时间浮动进行定义。

齿轮振动信号的仿真模型为

(25)

其中：Am为m倍齿轮啮合频率的幅值；fz(t)为齿轮转频随时间变化规律；φm为信号的初相角，设定为0；Z为齿数。

齿轮箱主动轮和故障轴承同轴，其参数设定如表1所示。

表1 仿真模型参数

为了验证前面所指出的基于FCF的阶比跟踪的不足，根据式(23)建立仿真模型，设置轴承的振动信号xbearing=0。根据表1参数得到如图3所示的时域波形图。使用基于FCF的阶比跟踪算法得到如图4所示的阶比谱，阶比谱中在1阶处出现峰值，然而，信号中并无轴承的振动信号成分。这是因为虽然轴承未发生故障，但是在包络时频图中有齿轮啮合频率成分，而且仅在时频图中无法判定此频率成分为GIMF还是FCF, 如果提取GIMF趋势线对信号进行角域重采样便会出现这种情况。因此，基于FCF的阶比跟踪算法可能会出现误判。

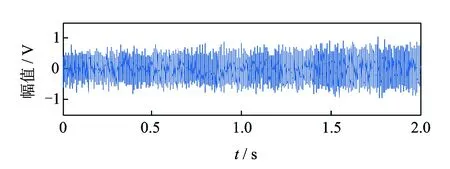
图3 正常轴承的仿真信号时域波形图Fig.3 Simulated signal of healthy bearing in time domain

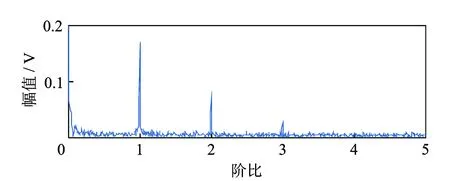
图4 故障特征阶比谱Fig.4 Order spectrum of fault feature

为了验证算法的有效性，根据表1参数建立的仿真模型得到如图5 所示时域波形图。图6给出了谱峭度图，从谱峭度图中看出，最大峭度值出现在尺度为7、中心频率为1 191 Hz处，而不是在设置中心频率为2 kHz(共振频率)处，这也直观反应了齿轮噪源干扰着共振频带的获取。为了提高CPP算法处理的效率，先对仿真信号降采样，然后使用CPP算法提取齿轮GIMF趋势线，根据GIMF估计转频，如图7所示。通过对比发现，估计转频与实际转频曲线基本吻合。根据估计转频对原信号进行等角度重采样，然后利用AR模型对角域信号进行滤波，得到如图8所示的滤波后信号。对滤波后信号进行Hilbert变换和FFT变换得到如图9所示的阶比谱，在阶比谱中阶比no=5.029处出现明显的峰值，与仿真信号的Co=5对应，由此可以判断轴承的外圈出现故障。

图5 仿真信号时域波形图Fig.5 Simulated signal in time domain

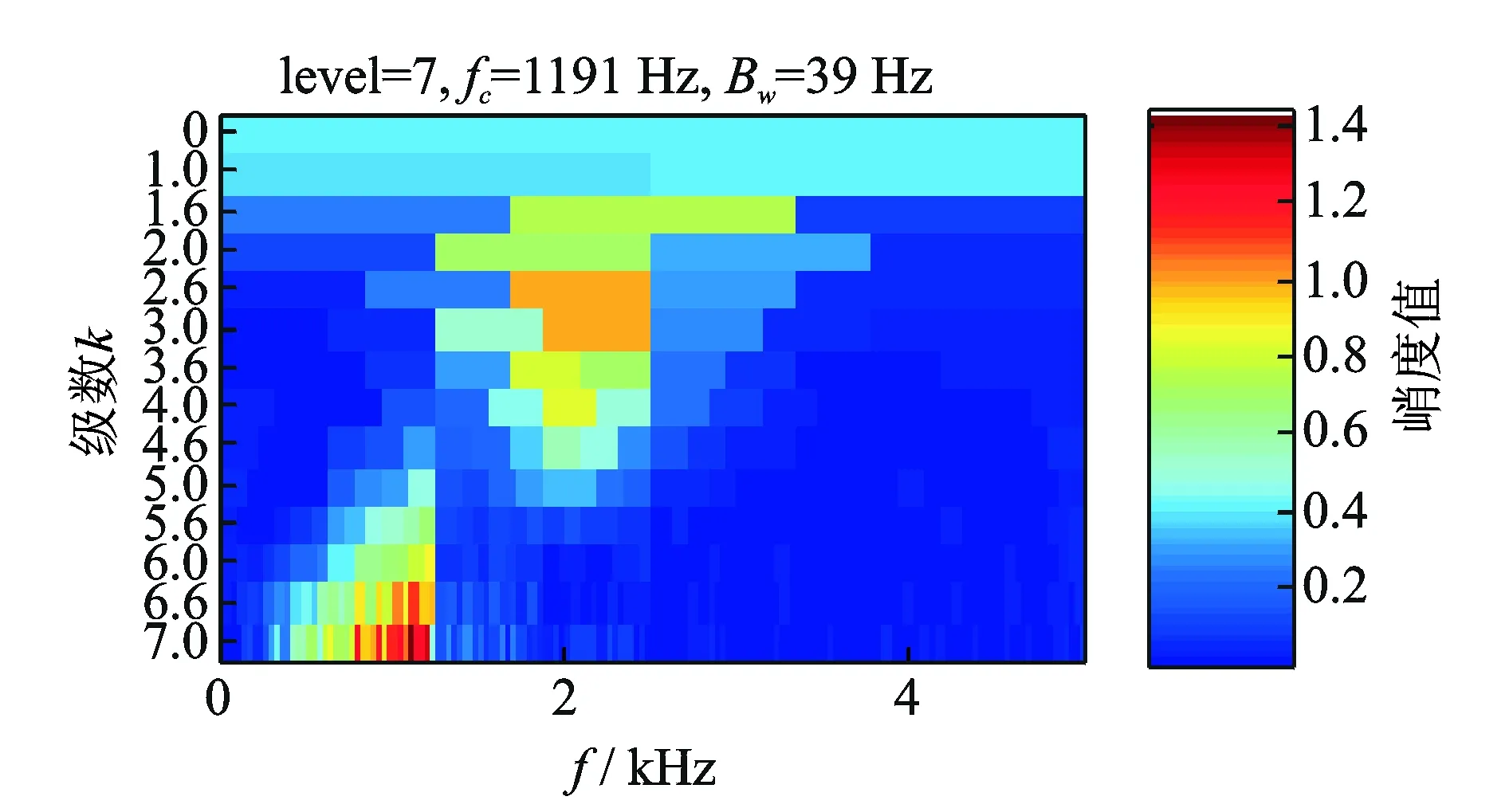
图6 仿真信号谱峭度图Fig.6 Simulation signal spectrum kurtogram

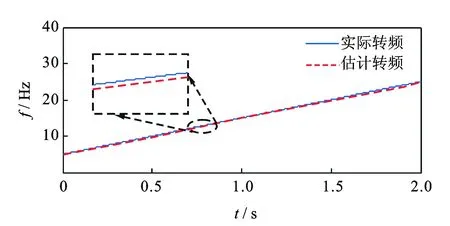
图7 仿真信号转频与等效转频Fig.7 Rotating frequency and equivalent rotating frequency

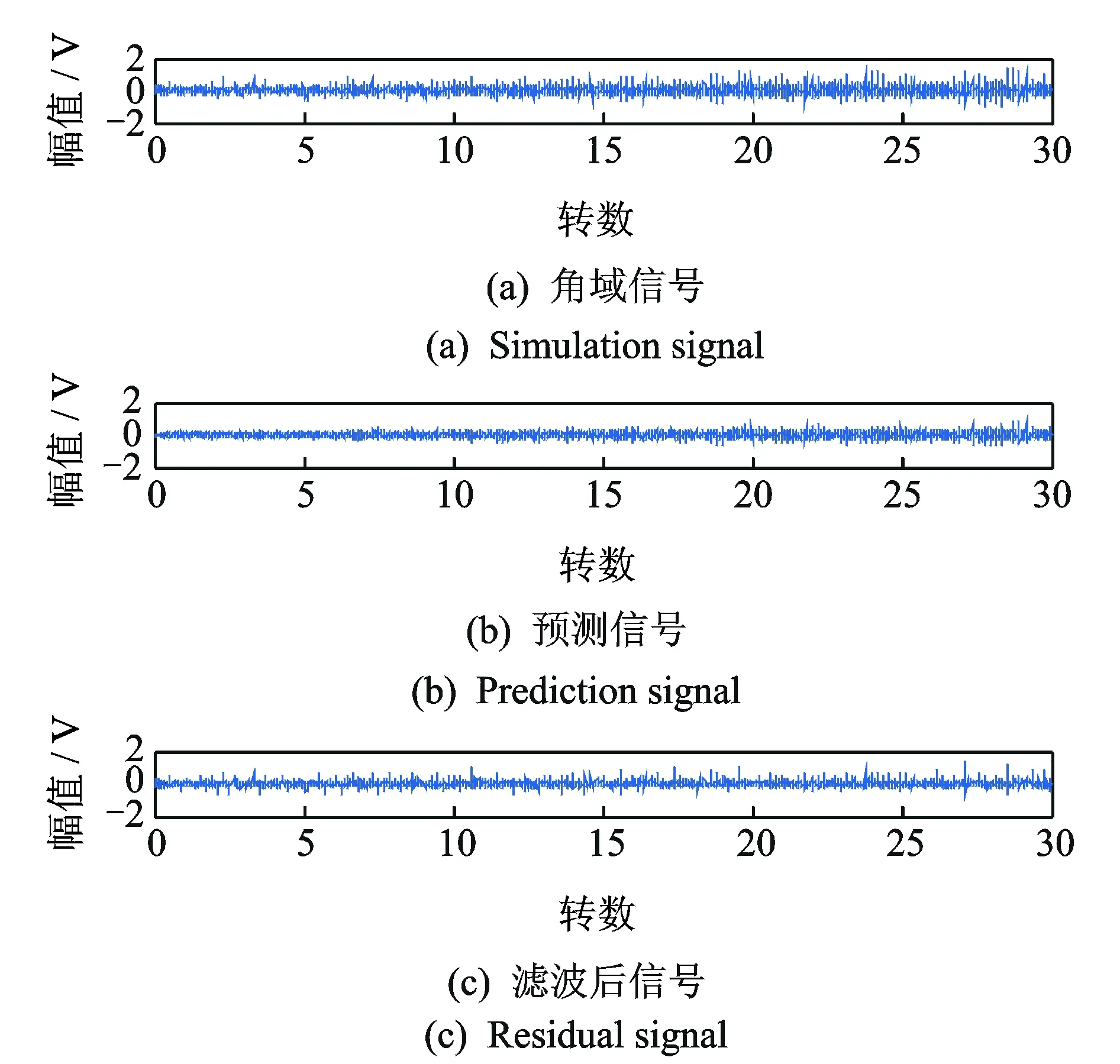
图8 仿真信号的滤波信号Fig.8 Filtering signal of the simulated signal

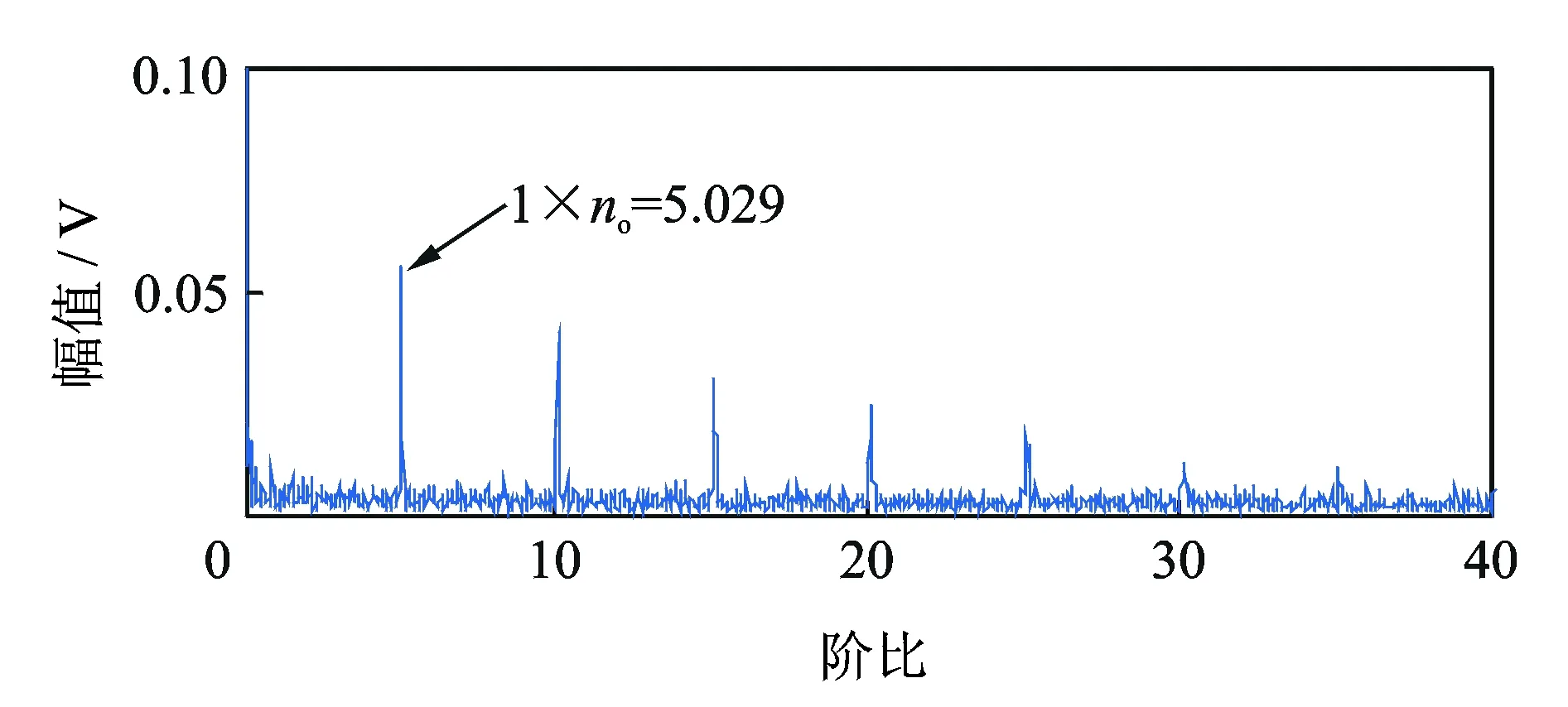
图9 仿真信号阶比谱Fig.9 Order spectrum of simulated signal

4 实测信号验证

利用如图10所示的实验台测得的外圈故障滚动轴承的振动信号对本算法进一步加以验证。实验轴承的参数如表2所示。

采集系统的采样率为24 kHz，截取时间段为2 s的数据。图11，12分别给出了时域波形图和谱峭度图。从谱峭度图中看出最大峭度值出现在尺度为

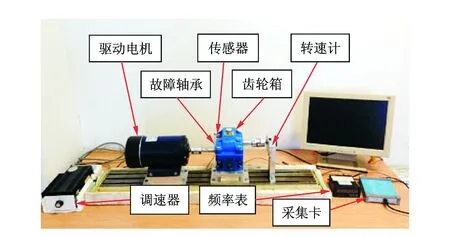
图10 试验台结构 Fig.10 Expcrimcntal set-up of the test rig

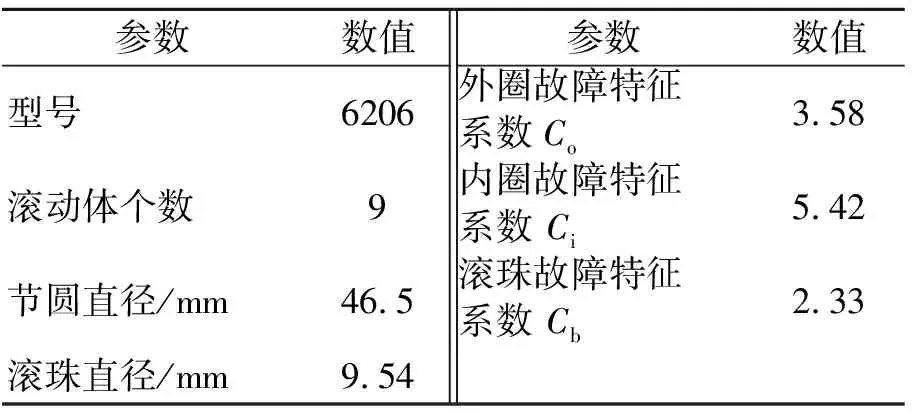
表2 滚动轴承结构参数

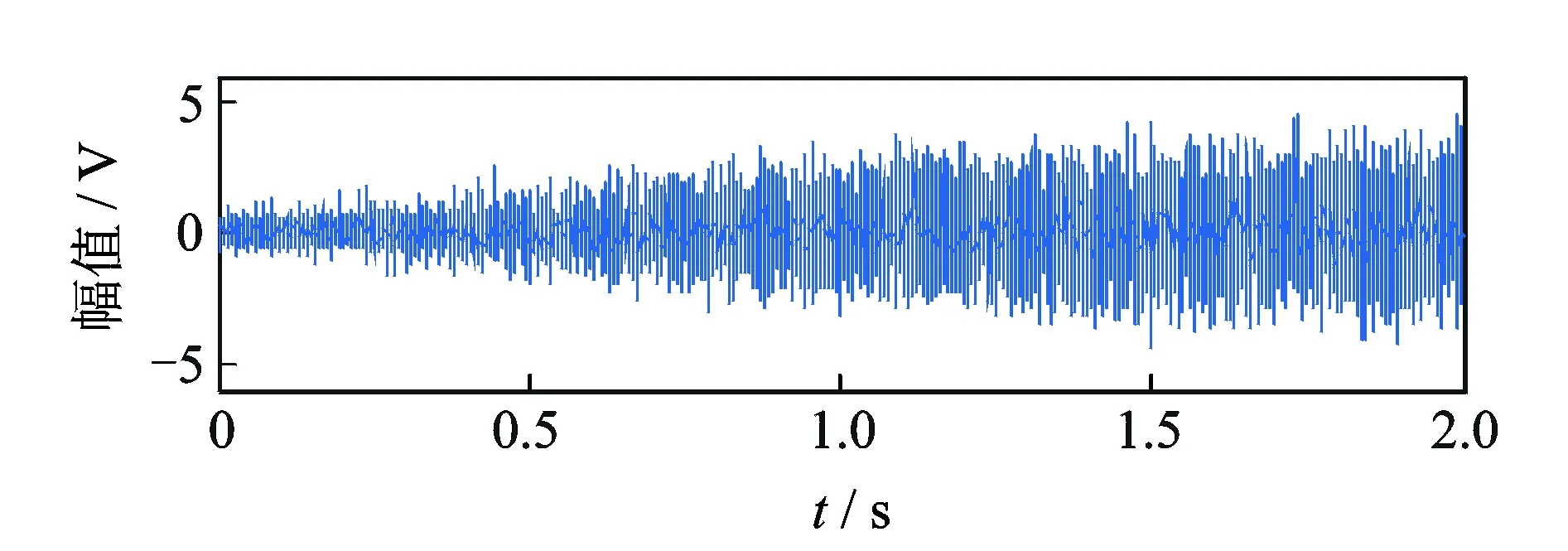
图11 外圈故障滚动轴承信号时域波形图Fig.11 Outer faulty bearing signal in time domain

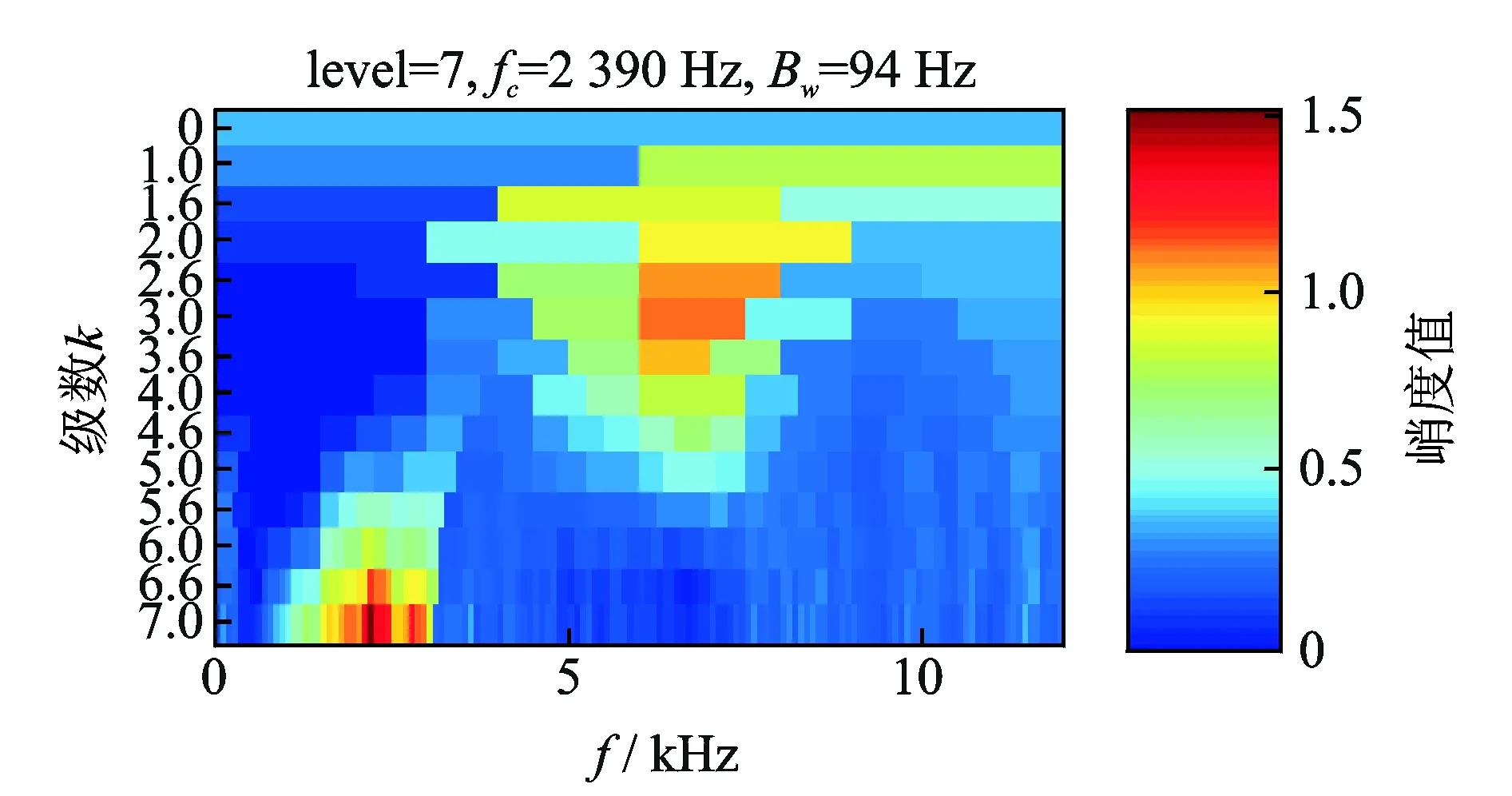
图12 外圈故障滚动轴承信号谱峭度Fig.12 Outer faulty bearing signal spectrum kurtogram

7、中心频率为2 390 Hz处，而不是在中心频率为6 kHz(共振频率)处。先对混合信号降采样，然后使用CPP算法提取GIMF趋势线，利用GIMF与轴承转速的关系，得到如图13所示的估计转频。根据估计转频对原信号进行等角度重采样，再利用AR模型对角域信号进行滤波，得到如14图所示的滤波后信号。对滤波后信号进行Hilbert变换和FFT变换得到如15图所示阶比谱，在阶比谱中阶比no=3.579处出现明显的峰值，正好与Co=3.58对应，由此可以判断轴承的外圈出现故障。

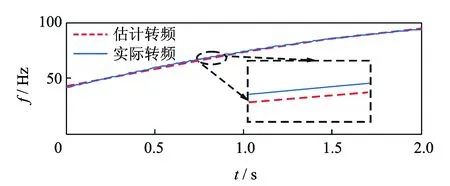
图13 外圈故障滚动轴承信号转频与等效转频Fig.13 Rotating frequency and equivalent rotating frequency

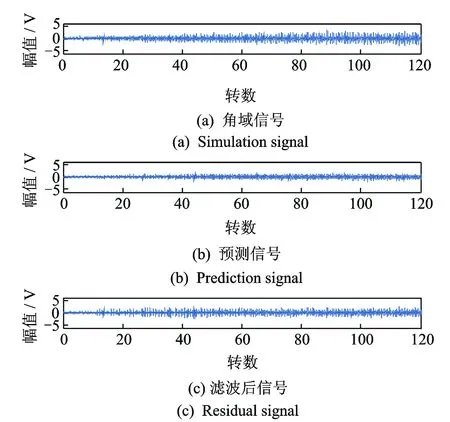
图14 外圈故障滚动轴承信号的滤波信号Fig.14 Filtering signal of outer faulty bearing signal

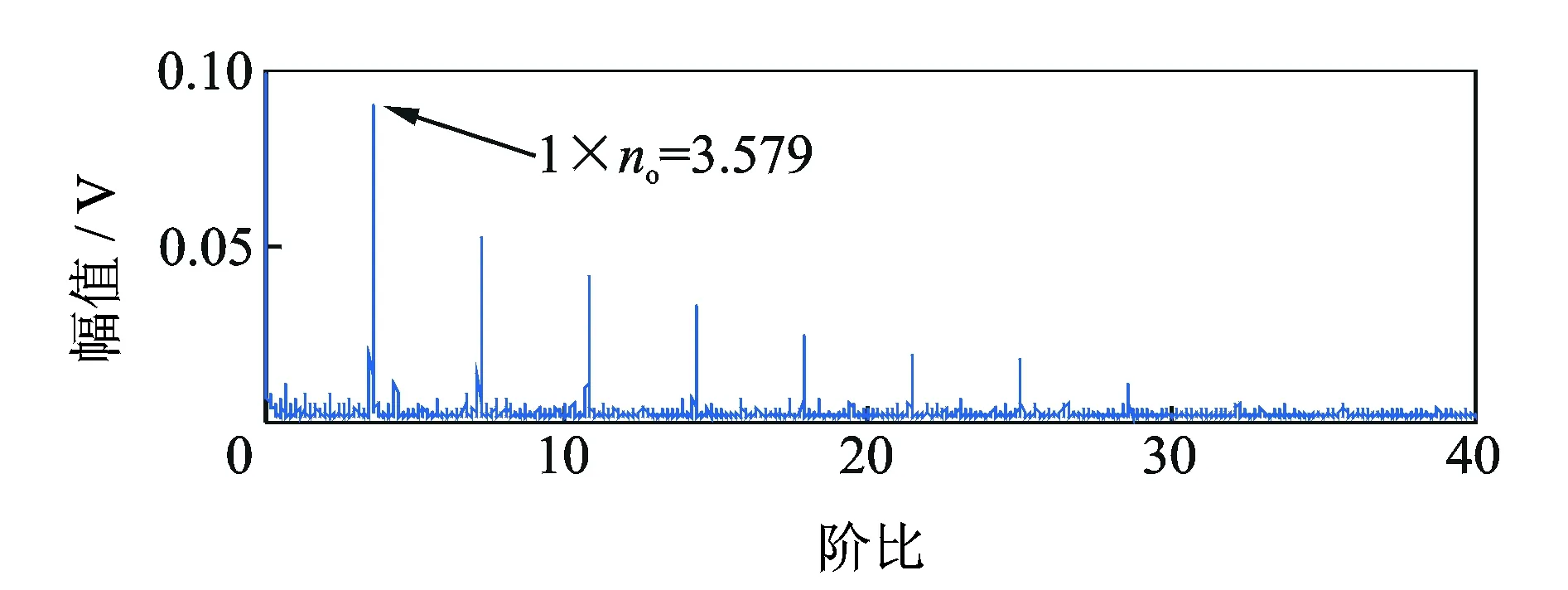
图15 外圈故障滚动轴承信号阶比谱Fig.15 Order spectrum of outer faulty bearing signal

5 结 论

1) 使用CPP算法提取降采样处理的齿轮噪源干扰下的振动信号的GIMF趋势线，并利用GIMF估计转频，根据估计转频对原混合信号进行等角度重采样，实现了时域信号到角域信号的转变。

2) 通过重采样恢复了齿轮啮合振动成分的周期性，使用AR模型可以滤除角域信号的齿轮啮合频率及其倍频成分。

3) 仿真信号和实测信号证明了使用GIMF趋势线估计转频的可行性，以及使用AR模型对角域信号滤波的有效性。

参 考 文 献

[1] 彭富强，于德介，武春燕. 基于多尺度线调频基稀疏信号分解的包络解调方法及其在齿轮故障诊断中的应用[J]. 机械工程学报, 2010, 46(12): 1-7.

Peng Fuqiang, Yu Dejie, Wu Chunyan. AM-FM signal extraction method by the sparse signal decomposition[J]. Journal of Mechanical Engineering, 2010, 46(12): 1-7. (in Chinese)

[2] 柏林，甄杰，彭畅，等. 变转速下滚动轴承阶比峭度图法故障特征提取[J]. 振动、测试与诊断, 2016, 36(4): 653-658.

Bo Lin, Zhen Jie, Peng Chang, et al. COT-kurtogram based fault features extraction for rolling element bearing under varying speed[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(4): 653-658. (in Chinese)

[3] 张亢，程军圣. 基于LMD和阶次跟踪分析的滚动轴承故障诊断[J]. 振动、测试与诊断, 2016,36(3): 586-591.

Zhang Kang, Cheng Junsheng. Roller bearing fault diagnosis based on LMD and order tracking analysis[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(3): 586-591. (in Chinese)

[4] Zhao Dezun, Li Jianyong, Cheng Weidong. Feature extraction of faulty rolling element bearing under variable rotational speed and gear interferences conditions [J]. Shock and Vibration, 2015(3): 1-9.

[5] Combet F, Zimroz R. A new method for the estimation of the instantaneous speed relative fluctuation in a vibration signal based on the short time scale transform[J]. Mechanical Systems and Signal Processing, 2009, 23(4): 1382-1397.

[6] 赵晓平，赵秀莉，侯荣涛，等. 一种新的旋转机械升降速阶段振动信号的瞬时频率估计算法[J]. 机械工程学报，2011, 47(7): 103-108.

Zhao Xiaoping, Zhao Xiuli, Hou Rongtao, et al. A new method for instantaneous frequency estimation of run-up or run-down vibration signal for rotating machinery[J]. Journal of Mechanical Engineering, 2011, 47(7): 103-108. (in Chinese)

[7] 郭瑜，秦树人，汤宝平，等. 基于瞬时频率估计的旋转机械阶比跟踪[J]. 机械工程学报, 2003, 39(3): 32-36.

Guo Yu, Qin Shuren, Tang Baoping, et al. Order tracking of rotating machinery based on instantaneous frequency estimation[J]. Chinese Journal of Mechanical Engineering, 2003, 39(3): 32-36. (in Chinese)

[8] 王天杨，李建勇，程卫东. 基于低次故障特征阶比系数的变转速滚动轴承等效转频估计算法[J]. 机械工程学报，2015, 51(3):121-128.

Wang Tianyang, Li Jianyong, Cheng Weidong. Equivalent rotational frequency estimation algorithm of faulty rolling bearing under varying rotational speed based on the lower fault characteristic order coefficient [J]. Journal of Mechanical Engineering，2015，51(3):121-128. (in Chinese)

[9] 王天杨，李建勇，程卫东. 基于改进的自适应噪声消除和故障特征阶比谱的齿轮噪源干扰下变转速滚动轴承故障诊断[J]. 振动与冲击, 2014, 33(18): 7-13.

Wang Tianyang, Li Jianyong, Cheng Weidong. Fault diagnosis of rolling bearing under a variable rotational speed and gear vibration noise based on revised ANC algorithm and FCO spectrum [J]. Journal of Vibration and Shock, 2014, 33(18): 7-13. (in Chinese)

[10] Candès E J, Charlton P R, Helgason H. Detecting highly oscillatory signals by chirplet path pursuit [J]. Applied and Computational Harmonic Analysis, 2008, 24(1): 14-40.

[11] 刘坚, 彭富强, 于德介．基于线调频小波路径追踪阶比跟踪算法的齿轮箱故障诊断研究[J]. 机械工程学报, 2009,45(7): 81-86.

Liu Jian, Peng Fuqiang, Yu Dejie. A new order tracking method based on chirplet path pursuit and its application to gearbox fault diagnosis[J]. Journal of Mechanical Engineering，2009,45(7): 81-86. (in Chinese)

[12] Robert B R, Sawalhi N. A comparison of methods for separation of deterministic and random signals[J].Condition Monitoring, 2011,1(1):11-43.

[13] 张西宁，吴婷婷，徐进杰. 变转速齿轮箱振动信号监测的无键相时域同步平均方法[J].西安交通大学学报, 2012, 46(6): 111-116.

Zhang Xining, Wu Tingting, Xu Jinjie. Time-domain synchronous average method without key-phase signal for vibration monitoring of variable speed gearbox [J]. Journal of Xi′an Jiaotong University, 2012, 46(6): 111-116. (in Chinese)

[14] 从飞云，陈进，董广明. 基于滚动轴承故障诊断的AR预测滤波器阶数问题研究[J]. 振动与冲击, 2012, 31(4) :44-47.

Cong Feiyun, Chen Jin, Dong Guangming. Order selection of AR predicting filter for rolling bearing diagnosis [J]. Journal of Vibration and Shock, 2012, 31(4):44-47. (in Chinese)

[15] 柏林，刘小峰，刘子军. 相关匹配在轴承故障诊断技术中的应用[J]. 振动、测试与诊断，2015,35(6)：1044-1048.

Bo Lin, Liu Xiaofeng, Liu Zijun. Technology of correlation matching for bearing fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(6)：1044-1048. (in Chinese)

[16] Liang M, Soltani B I. An energy operator approach to joint application of amplitude and frequency demodulations for bearing fault detection[J]. Mechanical Systems and Signal Processing, 2010, 24(5): 1473-1494.