车用直驱轮毂电机传感器故障诊断*
2018-08-01徐兴,陈特,陈龙,2
徐 兴 , 陈 特 , 陈 龙,2
(1.江苏大学汽车与交通工程学院 镇江,212013) (2.江苏大学汽车工程研究院 镇江,212013)
引 言
分布式驱动电动汽车4个驱动轮各由4个轮毂电机直接驱动,目前在电动汽车领域成为了许多研究者的关注重点[1-3]。由于其4个驱动轮输出力矩的瞬时控制易于实现,因此在电动汽车的高响应参数辨识、整车的横摆稳定性控制以及效率最优控制等方面都较传统汽车更有优势。安装于该车4个车轮上的轮毂电机的电流和转速可以利用传感器直接获取[4],然而由于环境因素的影响以及零部件老化等原因,电流、转速等传感器极易出现性能故障。一旦某一传感器发生故障,就会引起相应电控系统的监测不可靠及控制性能跃迁,降低系统的鲁棒性能,故这类系统传感器的故障诊断非常重要。
目前,传感器的故障诊断常见方法是利用传感器的冗余信息进行故障的辨识或定位。利用模型解析进行故障诊断的研究中,通常采取状态估计法,但状态估计受制于被控对象数学模型的精确程度,实际建模中要对模型的不确定性做近似化处理,且系统中存在一些未知输入的干扰及环境噪声等,这些不利因素均会导致诊断过程误报率的升高。为了处理上述问题,现有基于状态辨识研究的主要目的在于优化故障辨识方法对于模型不准确、未知干扰以及噪声等情形的鲁棒性和系统对于可能发生故障的敏感程度[5-10]。基于未知输入观测器的故障诊断方法已有许多研究成果[11-16]。Sedighi等[11]提出一种基于UIO的故障诊断方法。Mondal等[12]针对系统中存在的扰动和不确定性,研究了一种基于UIO的故障诊断方法。胡志坤等[16]考虑了一种存在未知输入和不确定噪声的系统模型,设计全阶UIO来实现对干扰的鲁棒性,得到了一种基于最优UIO的残差产生器。
针对电动汽车直驱电机系统同时含有未知输入和噪声的特征,进行传感器故障诊断的研究还不常见。卡尔曼滤波器是一种广泛应用于滤除高斯白噪声的递归滤波器,但不能对电动汽车直驱电机系统的未知输入和噪声有效分离。笔者通过系统降阶方法解耦研究对象的未知输入,并结合卡尔曼滤波算法,提出基于最优未知输入观测器设计鲁棒残差产生器,实现直驱电机系统电流、转速传感器故障诊断与定位,为分布式驱动电动汽车4个电机的转矩协调分配提供基础。
1 直驱轮毂电机系统数学模型
直驱轮毂电机输出轴上的动态转矩方程为
(1)
直驱轮毂电机等效电路的动态电压平衡方程为
(2)
其中:J为电机转子的转动惯量;b为阻尼系数;Kt为电机的转矩常数;TL为电机的输出作用力矩;i为轮毂电机的线电流;U0为轮毂电机的线电压;ω为轮毂电机的转速;R为轮毂电机绕组等效线电阻;L为轮毂电机绕组等效电感;Ka为反电动势系数。

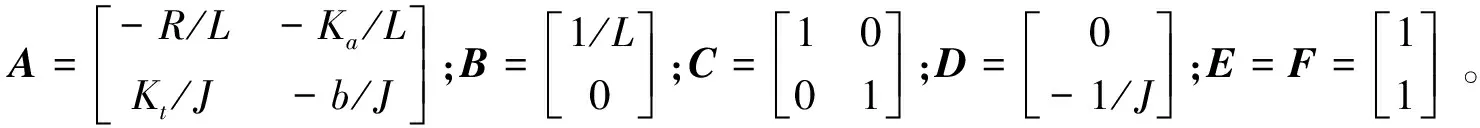
2 直驱电机系统传感器故障残差产生器设计
2.1 直驱电机系统未知输入解耦
直驱电机模型中,负载力矩是系统的未知输入量,可通过降阶将其与噪声解耦。根据式(3)、式(4)可知,rank(D)=1,满足条件rank(CD)=rank(D),表明需要解耦的未知输入的个数不超过实际情况下测量信号的个数,即系统满足观测器的匹配条件。构建一非奇异矩阵

(5)
则直驱电机模型式(3)、式(4)可转化为能观测规范型
其中:
2.2 基于最优UIO的鲁棒残差产生器设计
由式(8)、式(10)可得解耦后子系统的状态空间方程为
(12)
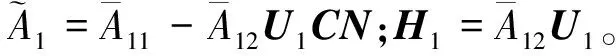
同理,由式(8)、式(10)可得另一子系统的状态方程为
(13)
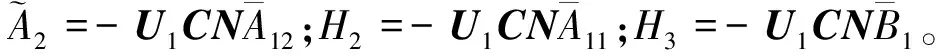
此时系统中不含未知输入。计算可得U11=0,即解耦后两子系统的测量输入y中只有转速传感器测得的电机转速为有效输入。
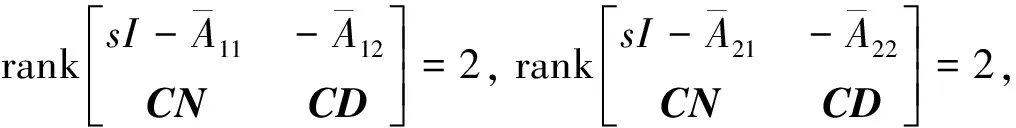
(14)
利用状态观测进行故障诊断研究时,残差的获取是实现故障检测的先决条件。当传感器出现故障,由式(4)可得直驱轮毂电机系统传感器故障模型为
y=Cx+Fv+f(t)
(15)
其中:f(t)为未知的传感器故障信号。
残差产生器的状态方程为
(16)
根据最优UIO输出的状态观测值yt,可得到残差信号ri(i=1,2)的幅值,该幅值可用于传感器故障检测。残差产生器设计流程如图1所示。
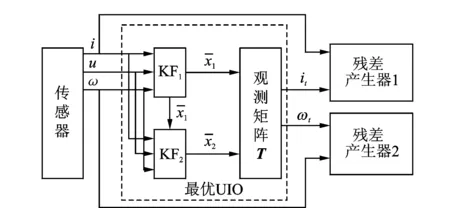
图1 残差产生器设计流程图Fig.1 The design flowchart of residual generator
由图1可知,针对含有未知输入和噪声干扰的直驱轮毂电机系统,设计的残差产生器将卡尔曼滤波算法和未知输入观测器的优点结合起来,能够提高残差识别的鲁棒性。
3 传感器故障诊断与定位
3.1 残差分析与阈值确定
一般情况下,传感器未发生故障时,残差ri应该基本趋近于零,当传感器存在故障时,残差就会远大于零。现实情况下,系统模型的精确度不可能完全达到理想的要求,传感器无故障时所得到的残差也不会完全维持在零值,因此,常见方法为利用阈值的方式实现残差信号的评估。为了减小模型固有的不精确性以及难以建模的环境因素带来的不良影响,采用极大似然比的方法来对残差信号进行评估。极大似然比估计的表达式为
(17)

若已知需要达到的误报率Pf,则阈值门限Tr的取值为
P{Ji>Tr|s=0}=Pf
(18)
其中:s=0表示不超过阈值;s=1表示超过阈值。
由已知的误报率,就能够通过查找χ2表来确定阈值门限。故障检测的逻辑为
(19)
3.2 传感器故障定位
式(12)、式(13)中,传感器测量输入y的有效输入只有转速,意味着所设计的最优未知输入观测器对电流传感器故障不敏感,对转速传感器故障敏感。当只有一个传感器出现故障时,如电流传感器,最优未知输入观测器不受故障信号的影响,能跟踪系统的实际状态,此时只有残差产生器1中残差信号的极大似然估计J1超过阈值范围,从而便可实现对电流传感器的故障定位。当转速传感器出现故障时,转速传感器测得的故障信息输入到最优未知输入观测器中,导致观测器估计的状态值都包含故障信息,则残差产生器1,2所输出残差信号的极大似然估计均超过阈值范围,此时便可决策出为转速传感器存在故障。故障定位逻辑如表1所示。

表1 故障定位逻辑
4 台架实验与验证
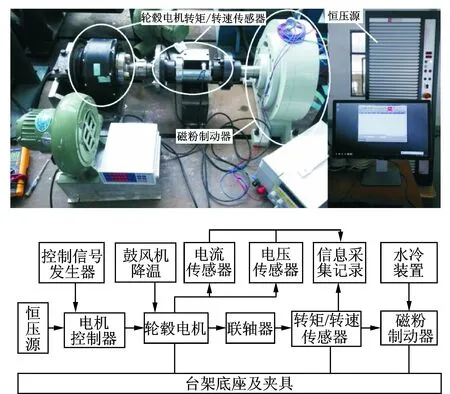
图2 实验台架Fig.2 The experiment bench
实验台架如图2所示。直驱轮毂电机、转速/转矩传感器以及磁粉制动器利用夹持装置固定于台架上,利用联轴器进行联结,使其在同一垂直高度上,从而实现同轴度标准。直驱轮毂电机由电机控制器直接控制,电机控制器的控制信号在1~3 V范围内,对应电机的转矩响应区间。为了监测直驱电机的工作状态,利用电压传感器和电流传感器记录电机控制器的输入电压与输入电流。实验时,迪卡龙电池测试系统作为恒压源给电机提供稳定电压,磁粉制动器用于施加负载,转速/转矩传感器用于测量记录不同给定控制信号下轮毂电机的转速与转矩,电机控制器控制信号的起步电压为1 V,每次增加0.2 V,直至信号电压达到3 V。
当传感器未发生故障时,将设计的最优UIO和一般的UIO两种观测器的残差信息进行比对,处理实验数据可得图3和图4。由图可知,传感器未发生故障时,基于最优UIO的残差处理信息比一般的UIO波动范围更小,稳定性更高,对精准的故障诊断更加具有优势。这说明笔者提出的残差产生器对系统噪声具有抑制作用,提高了残差的鲁棒性。
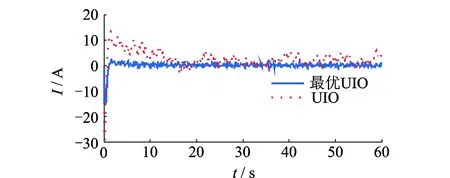
图3 无故障时电流传感器残差信号Fig.3 The current sensor residual signal without fault
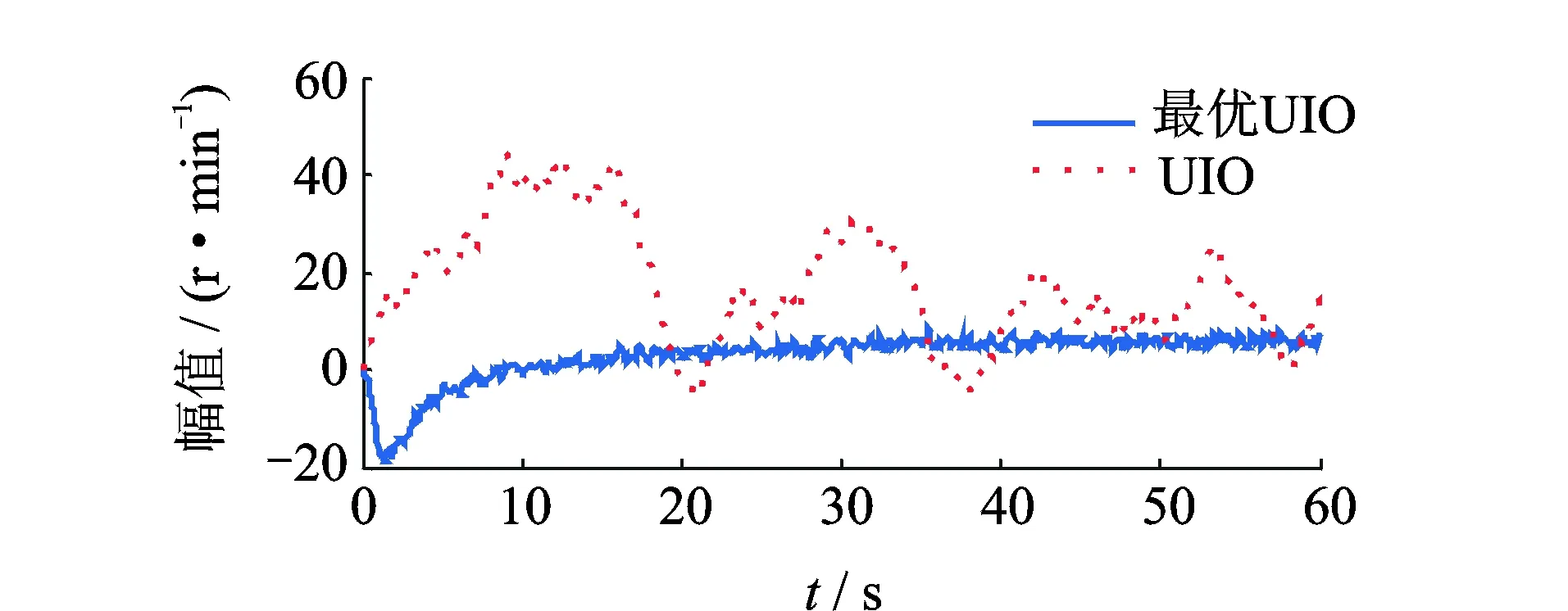
图4 无故障时转速传感器残差信号Fig.4 The speed sensor residual signal without fault
在t=400 s时分别模拟电流传感器故障和转速传感器故障,故障函数为
(20)
采取极大似然比的方法实现对残差信息的处理,选取Pf=0.000 1,根据χ2表可以得到Tr=15.137。根据上述算法对故障检测与定位进行验证。
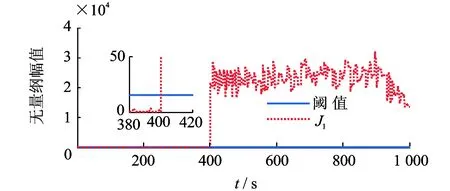
图5 电流传感器故障下的电流残差Fig.5 The current residual with the fault of current sensors
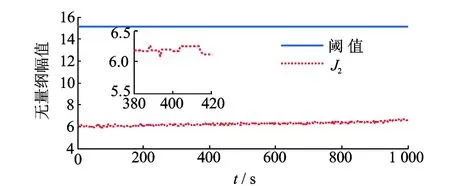
图6 电流传感器故障下的转速残差Fig.6 The speed residual with the fault of current sensors
当电流传感器发生故障时,实验结果如图5、图6所示。图5中,t=0~400 s时,电流残差GLR估计值一直在阈值范围内;t=400~1 000 s时,电流残差GLR估计值明显大于阈值。图6中,转速残差GLR估计值变化不大,一直保持在阈值范围内。通过对比两图,参考故障定位逻辑表,可定位出电流传感器存在故障。
当转速传感器发生故障时,实验结果如图7、图8所示。由图可知,t=0~400 s时,两传感器残差GLR估计值都保持在阈值范围内;t=400~1 000 s时,两传感器残差GLR估计值都明显大于阈值。参考表1,可定位出转速传感器存在故障。

图7 转速传感器故障下的电流残差Fig.7 The current residual with the fault of speed sensors

图8 转速传感器故障下的转速残差Fig.8 The speed residual with the fault of speed sensors
此外,受故障影响后的残差信号GLR估计值远大于故障前的残差信号GLR估计值,证明GLR方法的应用提高了残差信号对故障的敏感性。其中,由于电流信号波动较大,当电流传感器存在故障的时候,电流残差信号GLR估计的幅值相对较大,说明电流传感器对故障更敏感。
5 结 论
1) 最优未知输入观测器能够解耦未知输入,卡尔曼滤波器对噪声具有较好的抑制作用,使得残差产生器具有较强的鲁棒性。
2) GLR的运用增加了残差信息对传感器故障的敏感性,降低了故障的误报率。
3) 提出的传感器故障定位方法能够实现对直驱轮毂电机系统电流和转速传感器故障进行定位。
参 考 文 献
[1] 余卓平,冯源,熊璐. 分布式驱动电动汽车动力学控制发展现状综述[J].机械工程学报,2013,49(8): 105-114.
Yu Zhuoping, Feng Yuan, Xiong Lu. Review on vehicle dynamics control of distributed drive electric vehicle[J]. Journal of Mechanical Engineering, 2013,49(8): 105-114. (in Chinese)
[2] Yozo H. Future vehicle driven by electricity and control-research on four-wheel-motored“UOT electric march II”[J]. Vehicle System Dynamics, 2012, 50(9): 1473-1494.
[3] Kang Mingxin, Li Liang, Li Hongzhi, et al. Coordinated vehicle traction control based on engine torque and brake pressure under complicated road conditions[J].Vehicle System Dynamics, 2012, 50(9): 1473-1494.
[4] Cho W, Yoon J , Yim S, et al. Estimation of tire forces for application to vehicle stability control[J]. IEEE Transactions on Vehicular Technology, 2010, 59(2): 638-649.
[5] 周东华,刘洋,何潇. 闭环系统故障诊断技术综述[J].自动化学报, 2013, 39(11): 1933-1943.
Zhou Donghua, Liu Yang, He Xiao. Review on fault diagnosis techniques for closed-loop systems[J]. Acta Automatica Sinica, 2013, 39(11): 1933-1943. (in Chinese)
[6] Hwang I, Kim S, Kim Y. A survey of fault detection, isolation and reconfiguration methods[J]. IEEE Transactions on Control Systems Technology, 2010, 18(3): 636-653.
[7] Zhong Maiying, Ding S X,Lam J,et al.An LMI approach to design robust fault detection filter for uncertain LTI systems[J]. Automatica, 2003,39:543-550.
[8] 周公博,朱真才,陈光柱. 基于传感器网络的瓦斯传感器故障诊断[J]. 振动、测试与诊断, 2010,30(1): 23-27.
Zhou Gongbo, Zhu Zhencai, Chen Guangzhu. Fault diagnosis of gas sensor based on wireless sensor network[J]. Journal of Vibration, Measurement & Diagnosis, 2010,30(1): 23-27. (in Chinese)
[9] 张柯,姜斌. 基于故障诊断观测器的输出反馈容错控制设计[J].自动化学报, 2010, 36(2): 274-281.
Zhang Ke, Jiang Bin. Fault diagnosis observer-based output feedback fault tolerant control design[J]. Acta Automatica Sinica, 2010, 36(2): 274-281. (in Chinese)
[10] 刘晓东,钟麦英,柳海. 基于EKF的无人机飞行控制系统故障检测[J].上海交通大学学报, 2015, 49(6): 884-888.
Liu Xiaodong, Zhong Maiying, Liu Hai. EKF-based fault detection of unmanned aerial vehicle flight control system[J]. Journal of Shanghai Jiao Tong University, 2015, 49(6): 884-888. (in Chinese)
[11] Sedighi T, Koshkouei A J, Burnham K J. Nonlinear unknown input observer design for nonlinear systems: a newmethod[C]∥Preceedings of the 18th IFAC World Congress. New York, NY, USA: Elsevier, 2011: 11067-11072.
[12] Mondal S, Chakraborty G, Bhattacharyya K. LMI approach to robust unknown input observer design for continuous systems with noise and uncertainties[J]. International Journal of Control Automation and Systems, 2010, 8(2): 210-219.
[13] Chen W T, Saif M. Fuzzy nonlinear unknown input observer design with fault diagnosis applications[J]. Journal of Vibration and Control, 2010, 16(3): 377-401.
[14] 覃道亮,何凯,孔祥兴,等. 基于UIO的航空发动机控制系统传感器故障诊断[J].航空动力学报, 2011, 26(6): 1396-1404.
Tan Daoliang, He Kai, Kong Xiangxing, et al. UIO-based sensor fault diagnosis for aero-engine control systems[J]. Journal of Aerospace Power, 2011, 26(6): 1396-1404. (in Chinese)
[15] 钱华明,富振铎,宁秀丽,等. 系统干扰分布阵未知的GPS/SINS故障诊断算法[J]. 仪器仪表学报, 2013, 34(1): 208-214.
Qian Huaming, Fu Zhenduo, Ning Xiuli, et al. Fault diagnosis algorithm for GPS/SINS with unknown perturbation distribution matrix[J]. Chinese Journal of Scientific Instrument, 2013, 34(1): 208-214. (in Chinese)
[16] 胡志坤,孙岩,姜斌,等. 一种基于最优未知输入观测器的故障诊断方法[J].自动化学报, 2013, 39(8): 1225-1230.
Hu Zhikun, Sun Yan, Jiang Bin, et al. An optimal unknown input observer based fault diagnosis method[J]. Acta Automatica Sinica, 2013, 39(8): 1225-1230. (in Chinese)
