基于多尺度样本熵和VPMCD的自动机故障诊断*

王 斐， 房立清， 齐子元

(陆军工程大学石家庄校区一系 石家庄，050003)

引 言

高速自动机是高炮武器系统火力部分的核心部件，它是一个复杂的机械系统，工作过程中承受着高温、高压、高冲击过载等恶劣的环境。同时零部件众多，机构运动复杂，在长期工作后自动机零部件容易产生磨损、裂纹等故障，若不及时进行故障的排除，有可能在射击过程中造成严重后果。因此，对自动机进行状态监测与故障诊断十分重要[1-2]。

采用现代测试技术对自动机振动信号进行分析与识别是目前自动机故障诊断的重要方法。自动机是一种典型的复杂往复运动机械，针对自动机的故障诊断存在着以下难点：a.故障特征提取较为困难；所提取的自动机振动信号为非线性、非平稳的短时冲击非周期信号，同时伴随着大量干扰信号和环境噪声[3-4]，旋转机械中常用的时频域等分析方法效果不够理想；b.数据样本相对较少，故障识别率偏低；c.通过实弹射击的方式获得的数据，代价昂贵且数据样本量较少；d.采用传统的人工神经网络和支持向量机的方法进行故障识别存在识别率偏低的问题[5-6]。找到适用于自动机的故障特征提取方法，并利用有限的样本量获得较高的故障识别率是本研究所要解决的问题。

小波与小波包分析方法是自动机振动信号分析的常用方法，可以很好地对信号进行降噪及特征提取。样本熵是时间序列复杂度的一种度量，相比近似熵更具有相对一致性，近年来在分析信号序列的复杂度分析中已经获得成功应用，基于样本熵的特征提取方法广泛应用于机械系统的故障诊断当中。

Rao等[7]提出了一种多变量预测模型(VPMCD)，该方法利用从原始数据中提取的特征值之间的相互内在关系建立数学模型，用这些数学模型对被测试样本的特征值进行预测,把预测结果作为分类的依据，进一步进行模式识别。文献[8]通过实验验证了该方法能有效地应用于小样本多分类机械故障诊断，且在故障分类识别精度、计算复杂度、泛化推广能力、计算速度、鲁棒性以及可理解性等方面比神经网络、支持向量机具有更大的优势[9-11]。因此，VPMCD方法可以应用于小样本量的自动机故障诊断当中。

笔者将小波分析、多尺度样本熵和VPMCD方法相结合应用于自动机故障诊断当中，利用小波分析的方法对自动机原始振动信号进行降噪和分解，计算信号在多个尺度下的样本熵值，并选择最佳尺度因子，构造自动机振动信号的故障特征向量，最后采用VPMCD方法进行故障模式的识别。结果表明，该方法可以有效应用于高速自动机的故障诊断。

1 样本熵

样本熵通过衡量时间序列复杂性度量信号中产生新模式的概率大小，熵值越大时间序列复杂度越大。样本熵克服了数据偏差，具有很强的抗噪能力和优异的一致性，同时可采用较少的数据段即可得到稳定的熵值。样本熵具体计算过程[12]如下。

1) 对于一个N点时间序列{u(i):1≤i≤N}按顺序支起m维向量，其中i=1,2,…,N-m+1

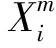
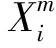
(i,j=1,2,…,N-m；i≠j)

4) 将矢量维度m改为m+1，得到Bm+1(r)

对于数据长度为N的样本，其对应的样本熵值S为

S(m,r,N)=In[Bm(r)/Bm+1(r)]

在计算样本熵的过程中，需要考虑到3个参数：嵌入维数m、相似度容限r及模糊函数的梯度n。根据文献[12]的研究结果，当m=1或2，r=0.1～0.25Std(Std 为时间序列数据u(i)的标准差) 计算得到的样本熵具有较为合理的统计特性。梯度n一般取较小的整数值，如2或3。综上分析，本研究中计算样本熵时，取m=2，r=0.2Std，n=2。

2 VPMCD方法

为了对故障特征值之间的内在变量关系进行定量描述，需要在特征值之间建立数学模型。VPMCD方法中提出了4种线性或非线性回归模型用以描述特征值Xi[13]。

线性模型

线性交互模型

二次交互模型

二次模型

其中:r≤p-1为模型阶数。

以p个特征值问题为例，以上述4种模型中任意一个模型，采用特征值Xj(j≠i)对Xi进行预测，都可以得到

Xi=f(Xj,b0,bj,bjj,bjk)+e

其中：特征值Xi称为被预测变量;Xj(j≠i) 称为预测变量;e为预测误差;b0,bj,bjj,bjk为模型参数，可通过训练样本数据对预测模型进行训练得到。

特征值Xi的变量预测模型VPMi，VPMCD建立的具体步骤见文献[8]。

3 基于多尺度样本熵和VPMCD的自动机故障诊断模型

采集的自动机的原始故障振动信号含有大量的干扰信号和背景噪声。首先，从原始信号中选取进行故障分析所需信号段以减少计算量；其次，利用小波阈值降噪的方法对信号进行降噪处理，完成对信号的预处理；然后，采用小波包分解的方法对降噪后的自动机振动信号进行分解，将其分解为多个不同尺度下的信号并计算不同尺度下信号的样本熵值，并选取对故障敏感的尺度因子所对应的样本熵值组成故障特征向量；最后，将故障特征向量通过VPMCD进行模式识别，从而完成自动机故障诊断。该诊断流程如图1所示。

图1 基于多尺度样本熵和VPMCD的故障诊断模型Fig.1 Fault diagnosis based on sample entropy and VPMCD

其具体步骤如下:

1) 信号预处理,采集自动机故障信号，根据自动机机构运动规律，从原始信号中提取有效的信号段，并对提取的故障信号进行小波阈值降噪，消除背景白噪声；

2) 小波包分解与重构,利用db4小波包对降噪后的信号进行3层分解，对分解得到的8个频带的序列进行重构，得到8个重构信号，每个信号包含了原始信号各个不同频段的信息，得到了8个尺度下的分解信号；

3) 故障特征提取,分别计算振动信号在不同尺度下的样本熵值Si(i=1,2,…，8)，比较故障的样本熵值，选取对故障较为敏感的尺度因子m，提取敏感尺度因子所对应的信号样本熵值Sm(m∈[1,8]),用所有Sm构造特征向量X,记为X=[x1,x2,…,xn](n∈[1,8])；

4 试验分析

炮闩作为高炮自动机的关键部件，在射击过程中承受着高温、高压、高过载等恶劣环境，容易出现磨损和裂纹等故障。笔者以某高炮导气式自动机为被测对象，根据运动规律分析和以往积累的经验，在自动机炮闩上设置3类典型故障，如图2所示。

图2 预置故障示意图Fig.2 Sketch map of the seeded fault

故障1：设置在炮闩闭锁过程中容易出现撞击而导致变形的部位，即在闭锁块被闩座的向前运动挤压和碰撞的面上设置点蚀故障，该位置一旦变形严重，则使得开闩时闭锁块不能完全收回而造成不能开闩。

故障2：设置在炮闩闭锁过程中由于摩擦而容易出现磨损的部位，即在闭锁快被闩座挤压而向外旋转的回转轴轴面上设置磨损故障，该处磨损后使闭锁块与闩体配合间隙增大，易造成关闩不到位。

故障3：在抓弹钩爪部设置局部裂纹故障，因为一旦射击过程中爪弹钩断裂，就不能正常抓紧和正确引导药筒，造成不能抛壳，容易与输弹线上的炮弹挤住卡死。

试验使用的振动信号采集系统包括三向压电式加速度传感器CA-YD-193A01，NI9234数据采集卡、NIcDAQ-9171机箱组成的数据采集模块和SignalPad测控软件，将加速度传感器安装在自动机支撑块附近，采集沿身管轴向的振动加速度信号。试验中采集沿身管轴向的正常(N)、点蚀(F1)、磨损(F2)、裂纹(F3)4种不同状态下的振动加速度信号，所得到信号如图3所示。由图3可知，试验中采集到的各状态下的原始振动信号中含有大量与自动机运动不相关的成分及背景噪声，这导致不同故障下的信号特征不明显。

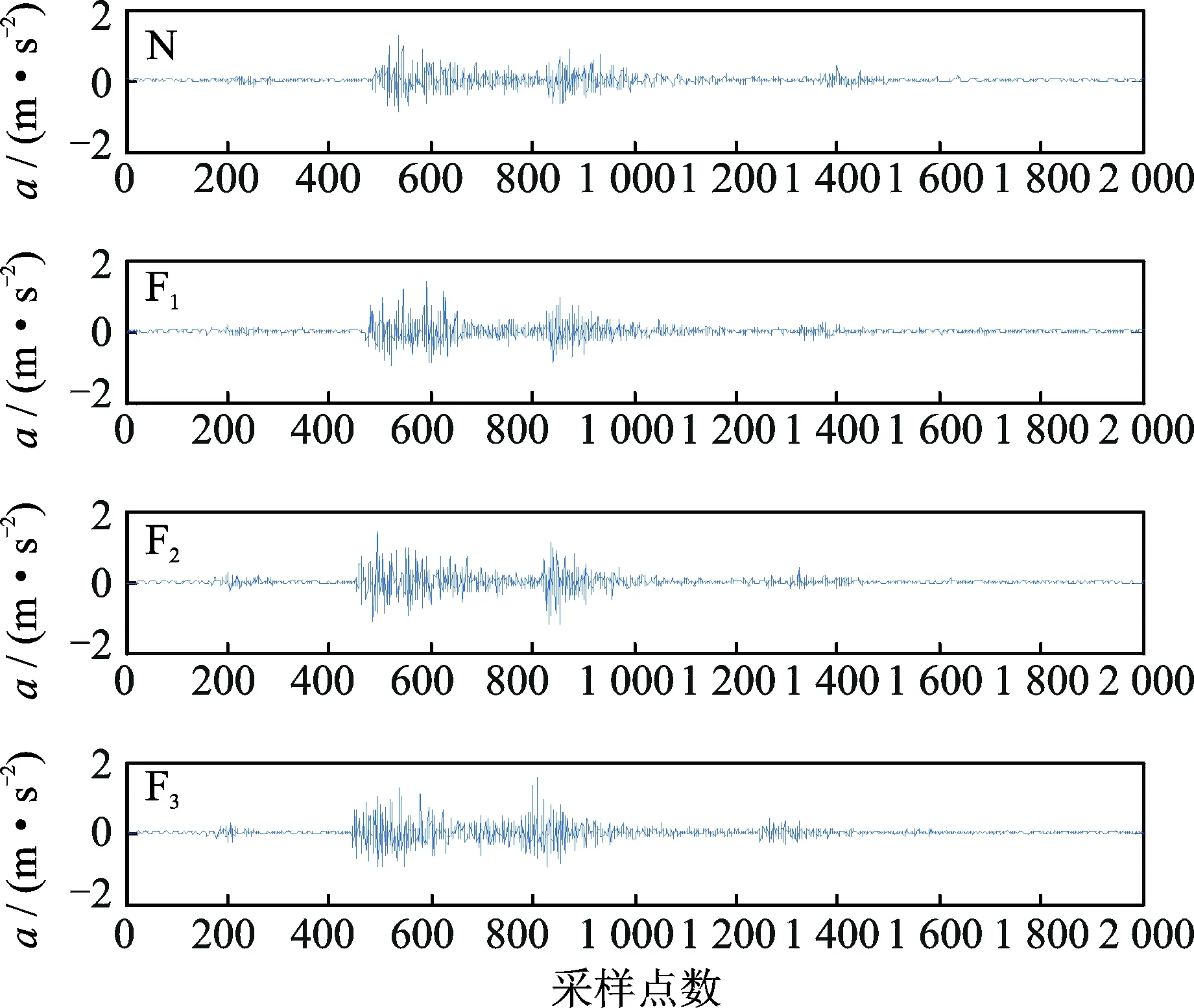
图3 4种状态下的自动机振动加速度信号Fig.3 Vibration signal of automata′s 4 states

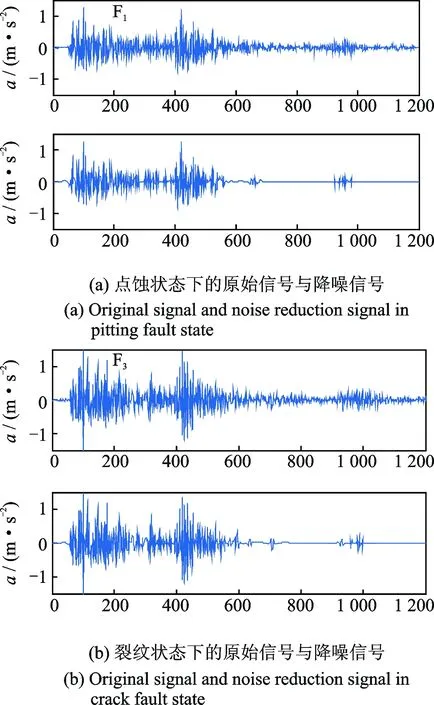
图4 降噪效果对比Fig.4 Denoise effect comparison

为了简化信号、降低计算复杂性及更好地提取信号的故障特征，根据高炮自动机机构运动规律，从原始信号中截取与炮闩运动相关的部分，并经小波阈值降噪的方法去除有效信号中的背景噪声，完成故障信号的预处理，最终得到降噪后的正常、点蚀、磨损、裂纹4种状态下的振动加速度信号。图4列出了点蚀(F1)和裂纹(F3)两种故障下的小波阈值去噪效果，通过比较降噪前后的截取信号可知，小波阈值去噪的方法可有效去除信号的背景噪声，提高信号的冲击特性。

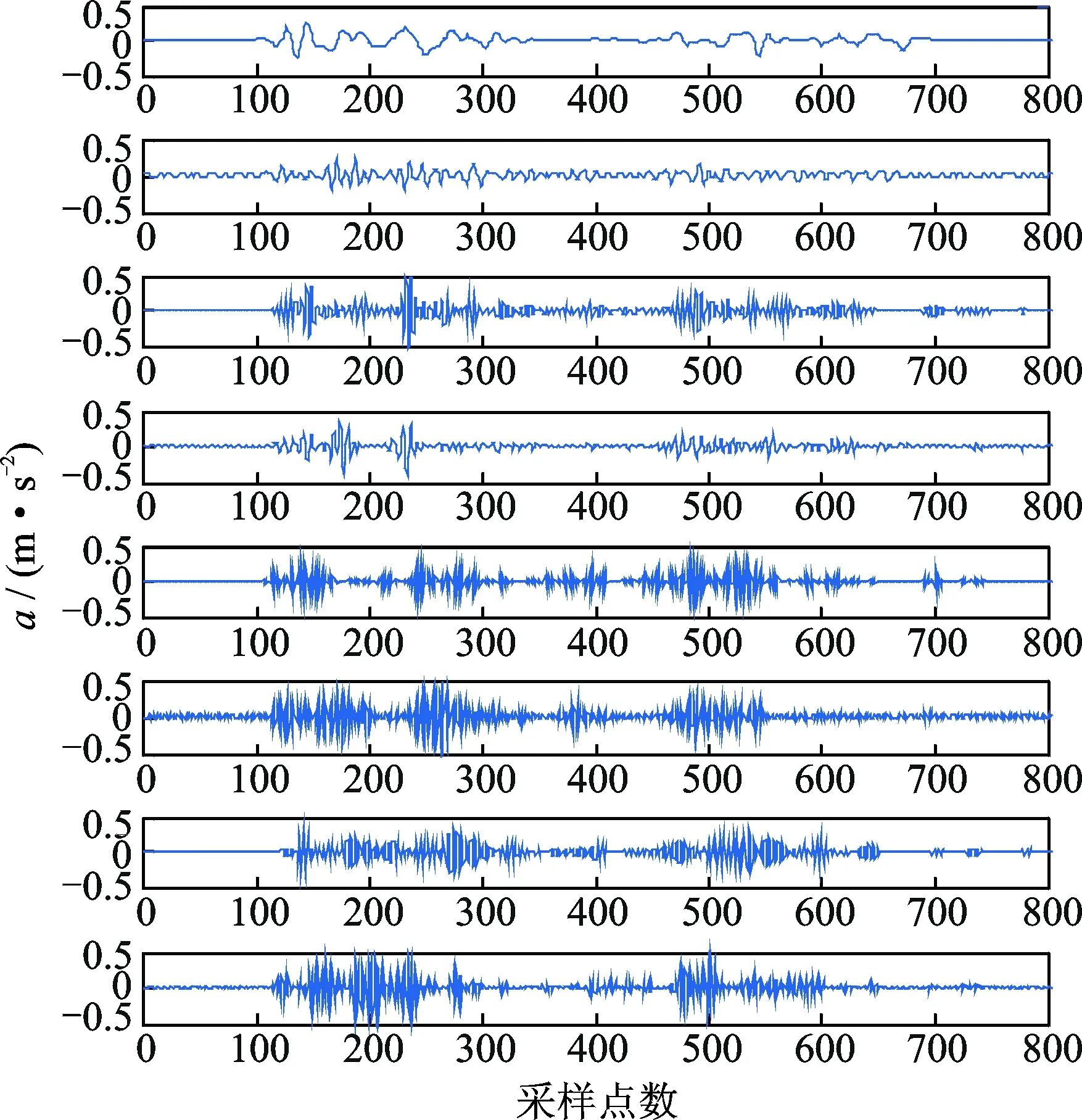
图5 故障1信号的3层小波包重构信号Fig.5 Wavelet packet reconstitution signals of fault 1

对原始信号进行预处理之后，采用db4小波对4种状态下的多组振动信号进行3层小波包分解，然后对分解后得到的8个频带的分解系数进行重构，得到8个重构信号，每个重构信号包含了原始信号在不同尺度下的振动信息。图5为故障1振动信号的第3层小波包分解结果，分别计算各状态的8个尺度下的小波包重构信号的样本熵值。图6为4种状态下的小波包样本熵均值的分布图。可以看出，不同尺度下的样本熵值对自动机故障的敏感程度有很大区别。尺度1，2下的样本熵值可以很好地区分4种故障状态；尺度3，5，7，8 下的信号样本熵不能有效区分正常、故障1和故障2等3种状态，且混叠较为明显；尺度4，6不能完全区分其中的两种故障状态。为了选取合适的自动机故障特征向量，简化计算复杂度并提高故障识别的准确性，经综合考虑，从中选取尺度1，2，4，6下所对应的样本熵值作为最终的自动机故障特征向量，进一步将特征向量输入多变量预测模型进行训练和识别。

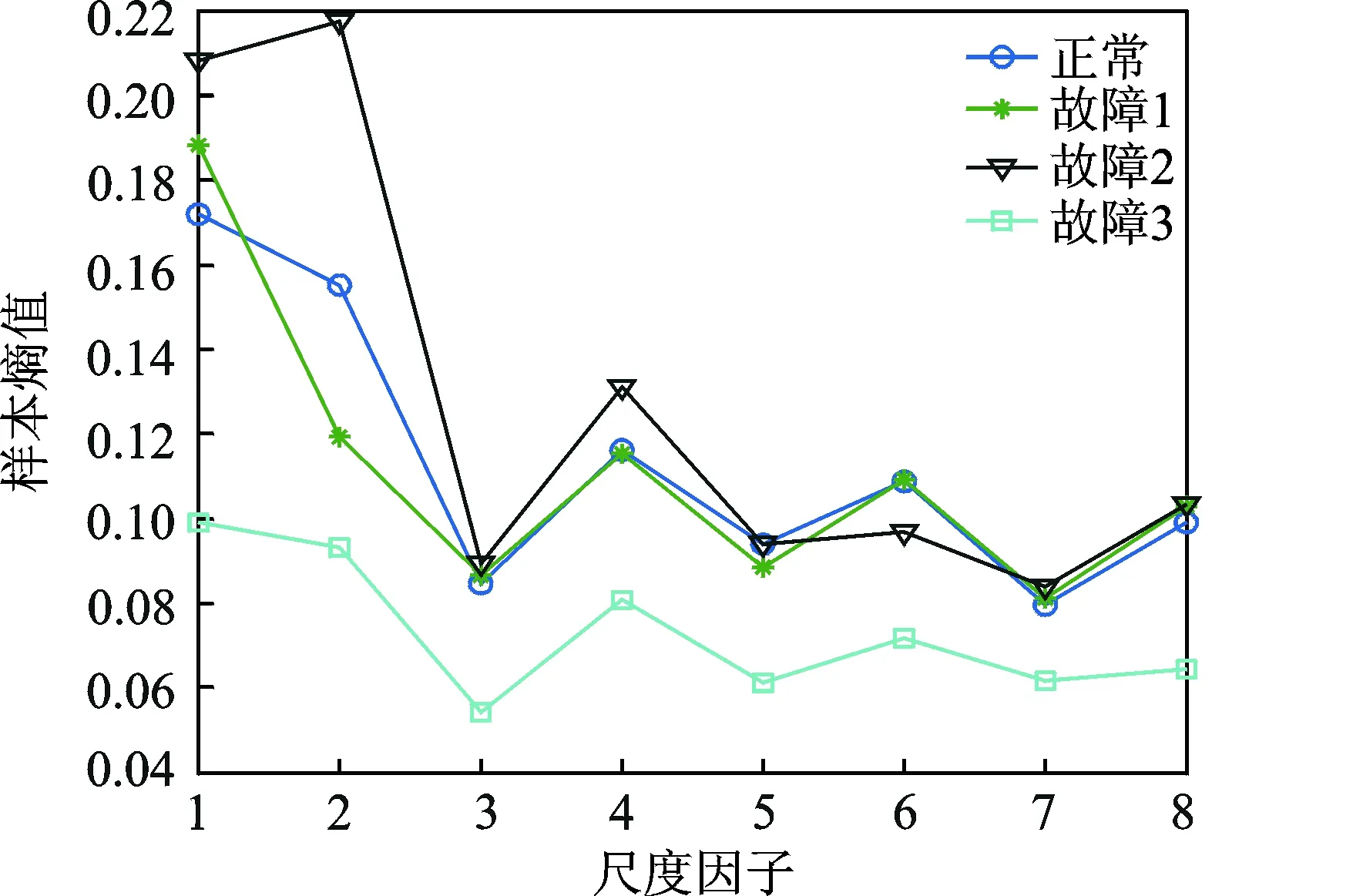
图6 小波包重构信号样本熵均值Fig.6 Distribution of average wavelet packet sample

分别选取正常、点蚀、磨损、裂纹4种状态下各10组特征向量作为训练样本训练VPM预测模型，模型选用二次交互模型。每种状态各10组特征向量作为测试样本，得到表1所示的VPM预测模型系数。利用训练得到的VPM对4种态对应的测试样本进行模式识别判断，识别结果全部正确，并且测试样本经不同状态对应的VPM处理后，得到的误差平方和差别明显，模式极易区分。表2列出了部分测试样本的测试识别结果。

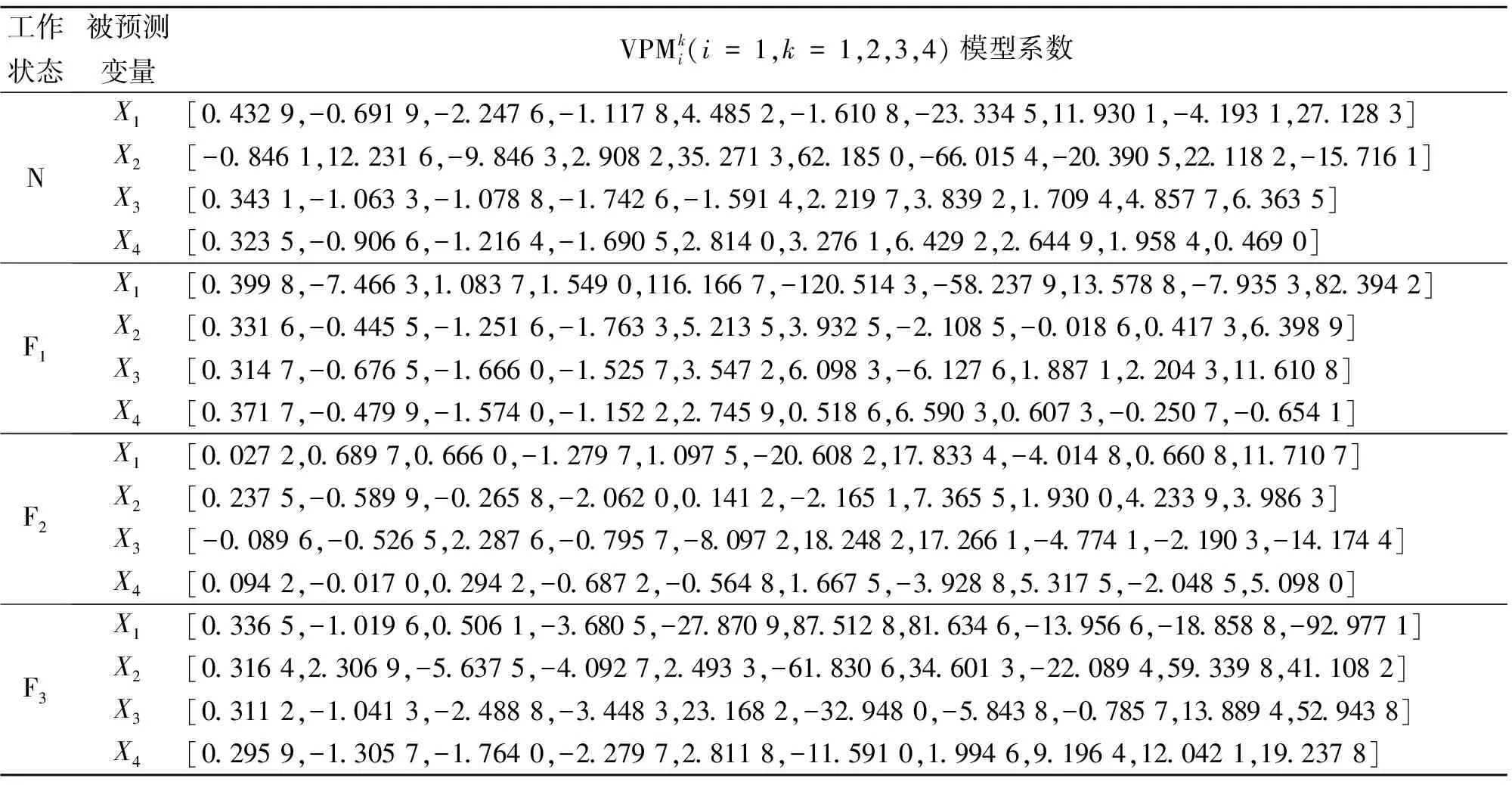
表1 自动机不同状态下的VPMCD预测模型的模型系数

表2 基于VPMCD的自动机故障诊断部分结果

为了说明VPMCD方法的优势，将故障特征向量输入支持向量机(SVM)中进行识别，10组样本作为训练样本，10组样本作为测试样本，其测试识别结果如表3所示，支持向量机方法总的识别结果仅为为82.5%。这也说明了小样本量情况下VPMCD方法更具有优势。

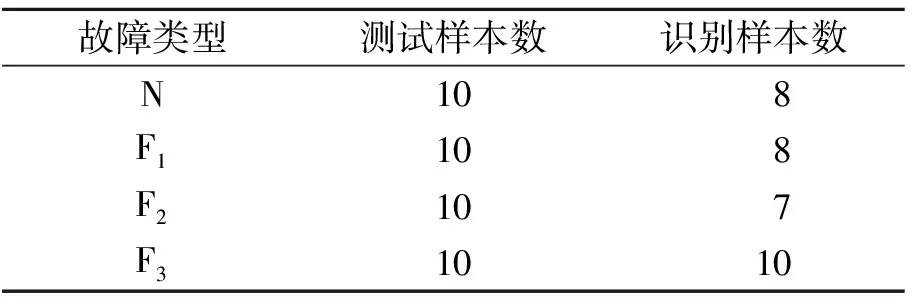
表3 支持向量机对4种工作状态样本的测试结果

5 结束语

VPMCD方法利用原始信号数据中所提取的特征值之间的相互内在关系建立数学模型进行模式识别，能够很好地解决小样本数据下的模式识别问题。笔者针对高炮自动机故障特征较难提取及小样本情况下故障识别率偏低的问题，将小波分析、样本熵、多尺度熵及VPMCD方法相结合，提出了基于多尺度样本熵和VPMCD的自动机故障模式识别方法。通过设置自动机零件的多种典型故障并进行试验分析，验证了所提方法的有效性。同传统的支持向量机模式识别方法的比较结果也充分说明，该方法可以有效解决基于小样本量的自动机故障诊断问题。

参 考 文 献

[1] 田园,潘宏侠,陈玉青,等. 应用S.L.Peng窄带分解与广义分形的自动机故障诊断[J]. 中国测试, 2016, 42(2): 100-104.

Tian Yuan，Pan Hongxia，Ceng Yuqing，et al. Automaton fault diagnosis based on S.L.Peng local narrow-band decomposition and generalized fractal theory [J]. China Measurement & Test, 2016, 42(2): 100-104. (in Chinese)

[2] 许昕,潘宏侠,潘铭志. 独立分量分析在自动机振动信号处理中的应用[J]. 振动、测试与诊断, 2016, 36(1): 120-125.

Xu Xin, Pan Hongxia,Pan Mingzhi. Application of independent component analysis in automata vibration signal process[J].Journal of Vibration，Measurement & Diagnosis, 2016, 36(1): 120-125. (in Chinese)

[3] 潘宏侠,都衡,马春茂. 局域波信息熵在高速自动机故障诊断中的应用[J]. 振动、测试与诊断, 2015, 35(6): 1159-1164.

Pan Hongxia, Du Heng, Ma Chunmao. High-speed automaton fault diagnosis based on local wave and information entropy[J]. Journal of Vibration，Measurement & Diagnosis, 2015, 35(6): 1159-1164. (in Chinese)

[4] 潘宏侠,兰海龙,任海峰. 基于局域波降噪和双谱分析的自动机故障诊断研究[J].兵工学报, 2014, 35(7): 1077-1082.

Pan Hongxia，Lan Hailong，Ren Haifeng. Fault diagnosis for automata based on local wave noisereduction and bispectral analysis[J]. Acta Armamentarii，2014, 35(7): 1077-1082.(in Chinese)

[5] 潘宏侠,马百雪,许昕. 基于小波尺度谱重排与小波排列熵的自动机故障诊断[J]. 火炮发射与控制学报, 2015, 36(2): 64-67.

Pan Hongxia，Ma Baixue，Xu Xin. Fault diagnosis of automatic cannon based on wavelet scalogram rearrangement and permutation entropy [J].Journal of Gun Launch & Control,2015,36(2):64-67. (in Chinese)

[6] 李莎,潘宏侠,都衡. 基于EEMD信息熵和PSO_SVM的自动机故障诊断[J].机械设计与研究, 2014, 30(6): 26-29.

Li Sha, Pan Hongxia, Du Heng. Automaton fault diagnosis based on information entropy and PSO-SVM [J]. Machine Design and Research, 2014, 30(6): 26-29. (in Chinese)

[7] Rao R, Samavedham L. Variable predictive models—a new multivariate classification approach for pattern recognition applications[J].Pattern Recognition, 2009, 42(7): 7-16.

[8] 罗颂荣,程军圣,郑近德,等. GA_VPMCD方法及其在机械故障智能诊断中的应用[J]. 振动工程学报, 2014, 27(2): 289-294.

Luo Songrong, Cheng Junsheng, Zheng Jinde,et al. GA-VPMCD method and its application in machineryfault intelligent diagnosis [J]. Journal of Vibration Engineering, 2014, 27(2): 289-294. (in Chinese)

[9] 程军圣,马兴伟,杨宇.基于VPMCD和EMD的齿轮故障诊断方法[J]. 振动与冲击,2013, 32(20): 9-13.

Cheng Junsheng, Ma Xingwei,Yang Yu. Gear fault diagnosis method based on VPMCD and EMD [J].Journal of Vibration and Shock, 2013, 32(20): 9-13. (in Chinese)

[10] 杨宇,李永国,程军圣. WVPMCD及其在滚动轴承故障诊断中的应用[J]. 湖南大学学报, 2014, 41(2): 52-57.

Yang Yu, Li Yongguo, Cheng Junsheng. Weighted least square-VPMCD and its applicationin roller bearing fault diagnosis[J]. Journal of Hunan University, 2014, 41(2): 52-57. (in Chinese)

[11] 程军圣,郑近德,杨宇. 变量预测模型在齿轮故障诊断中的应用[J].振动、测试与诊断,2013,33(1):111-114.

Cheng Junsheng,Zheng Jinde,Yang Yu. Variable predictive model based class discriminate applicationin gearing fault diagnosis [J]. Journal of Vibration，Measurement & Diagnosis, 2013, 33(1): 111-114. (in Chinese)

[12] 成娟,陈勋,彭虎. 基于样本熵的肌电信号起始点检测研究[J]. 电子学报, 2016, 44(2): 479-484.

Cheng Juan, Chen Xun, Peng Hu.An onset detection method for action surface electromyography based on sample entropy[J].Acta Electronica Sinica, 2016, 44(2): 479-484. (in Chinese)

[13] Yang Yu, Wang Huanghuang, Cheng Junsheng, et al.A fault diagnosis approach for roller bearing based on VPMCD under variable speed condition[J].Measurement, 2013, 46(2): 2306-2312.