基于模糊C-均值的空间机构轴系健康评估方法*
2018-08-01刘红星周宁宁
刘红星, 卿 涛, 王 虹, 周宁宁
(北京控制工程研究所精密转动和传动机构长寿命技术北京市重点实验室 北京,100094)
引 言
空间精密轴系是飞轮、控制力矩陀螺等空间高速机构的核心部件之一,具有旋转精度高、精度等级高(P4级以上)、寿命长(8~15年)等特点[1],在工作过程中健康状态变化不显著。空间精密轴系多设计为弹流润滑,尚无广泛认可的加速寿命试验方法,其寿命试验只能采取1∶1的实时寿命试验[2],获取其全寿命周期测试数据的时间长,成本高。
随着航天领域对空间轴系提出更高精度、更长寿命需求,其健康监测成为重要研究内容,而健康状态评估是其中的难点之一。振动监测被广泛应用于轴承健康监测,相关评估方法有基于高斯混合模型[3]、神经网络[4]、隐马尔科夫模型[5]及模糊C-均值[6-10]等方法,都是通过对单个轴承全寿命周期健康变化规律的拟合来实现健康状态评估的,这对于空间精密轴系来说,应用难度很大。
针对上述情况,考虑到基于模糊C-均值的评估方法具有算法简单、结果可解释性强的优点[8],提出了一种基于模糊C-均值聚类的空间轴系健康评估方法,该方法不同于文献[6-10] 中利用单个轴承全寿命周期数据开展健康评估的方法,而是利用多个典型子样,根据被评估子样与典型子样间的特征相似性得到直观的亲疏程度结论,实现健康状态评估,从而避免了获取轴系全寿命周期测试数据时间长、成本高的难题。该方法定义了新的频域无量纲特征参数——特征谱线明显度,通过优良和故障两类轴系的特征参数训练聚类模型,得到被评估轴系对优良轴系类的隶属度,最后基于隶属度构造了健康指数,实现空间轴系健康状态量化评估。
1 模糊C-均值聚类算法
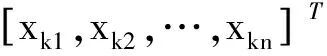
其中:vi为第i类的聚类中心矢量;μik为第k个样本对第i类的隶属度。
μik满足约束条件
(3)
FCM聚类算法基于使目标函数最小化的原理[12],该目标函数指Dunn定义的C-均值函数
(4)
其中:Dik为欧氏距离。
其定义式为
(5)
式(4)的最小化是一种非线性优化问题,FCM聚类准则是在约束条件下,通过求J(X;U,V)对U和V的偏微分,并运用拉格朗日乘数法,寻求最佳(U,V),使式(4)最小[12]。最佳(U,V)中元素为
(6)
(7)
其中:m为平滑参数控制类间划分的模糊度[8],该参数越大,类间的划分越模糊,反之则划分越明确,一般取1≤m≤5;vi为划分到某一类的样本的加权平均,权重是样本对于该类的隶属度μik。
2 轴系健康评估方法
2.1 特征参数提取
特征参数提取会在很大程度上影响轴系健康状态评估的准确度,由于多参数比单参数具有更好的容错性,且时域和频域参数存在一定的信息互补,同时考虑到无量纲特征参数可减小不同轴系间由于轴承尺寸、预载及振动测试时轴承转速的差异等造成的影响[13],因此,在时域和频域分别提取对轴系健康状态差异敏感性较强的无量纲特征参数,构造多参数输入以开展轴系健康状态评估。
在多数情况下,峭度在轴承振动信号时域无量纲特征参数中,对轴系状态差异敏感性较强[13],在此将峭度应用于轴系健康状态评估,对于信号Y=[y1,y2,…,yN],其峭度(K)[14]定义为
(8)
其中:μ,σ分别为信号Y的均值和标准差。
对于轴系振动信号的频域特征参数,尚无广泛采用的无量纲参数,在此基于包络频谱中特征频率定义新的无量纲参数。空间精密轴系在长期工作过程中会发生滚动表面状况的变化,主要变为轴承滚珠、内圈及外圈的表面缺陷,这会引起包络频谱在三者的特征频率及其倍频处的幅值显著增大。滚动轴承的滚珠、内圈和外圈的振动特征频率fb,fic,foc的计算公式[13]为
(9)
(10)
(11)
其中:D为轴承节圆直径;d为滚动体直径;α为接触角;Z为滚珠个数;fo为外圈转动频率,fi为内圈转动频率。
在上述特征频率及其倍频中,前3倍频幅值相对显著,而前3倍频在包络频谱中的幅值明显程度可反映缺陷的严重程度。基于此,定义新的无量纲频域特征参数——特征谱线明显度(Dc),其思路如下:
1) 分别计算包络频谱中滚珠、内圈和外圈特征频率的前3倍频的能量和;
2) 综合考虑频段选取的对称性和加速度传感器的频响范围,选取包络频谱中特征频率的0.5~3.5倍频间频段,计算频段能量和;
3) 分别计算各特征频率的前3倍频能量和与对应频段能量和的比值,以三者代数和作为Dc。
Dc定义式为
(12)
其中:S(ifb),S(ific),S(ifoc)分别为包络频谱在滚珠、内圈和外圈特征频率的第i倍频处的幅值;S(k)为频率k处的谱线幅值。
从Dc的定义可看出,该参数反映了轴承总体缺陷程度。理论上,总体缺陷越严重,该值越接近于3,反之越接近于0。
2.2 健康指数计算
2.2.1 健康指数的定义
为实现空间精密轴系的定量化健康评估,需构造理论上可解释的健康指数,而FCM聚类模型输出的隶属度反映了非线性优化后样本与聚类中心的接近程度,可解释性强[8]。若取优良轴系和故障轴系两类数据样本对FCM聚类模型进行训练,将待评估轴系对优良轴系类的隶属度均值化和归一化计算健康指数H,该指数可在一定程度上反映轴系的健康状态,其定义式为
(13)
其中:μb,μf,μg分别为待评估轴系、故障轴系、优良轴系的样本数据对“优良轴系类”的隶属度的均值。
从该定义可看出,轴系的健康状态越好,健康指数越接近于1,反之越接近于0。
2.2.2 健康指数的计算流程
健康指数计算以FCM聚类模型作为重要工具,具体计算流程如下。
1) 特征参数提取:对振动信号共振解调获得包络频谱,根据式(8)~式(12)提取优良轴系、故障轴系和待评估轴系振动信号的峭度(K)和特征谱线明显度Dc。
2) 参数归一化:将各轴系的特征参数做归一化处理,以便于计算。
3) 输入样本分类:将优良轴系和故障轴系振动信号的(K,Dc)分别作为一类,待评估轴系振动信号的(K,Dc)作为一类,并保证前两者样本数目多于第三者。

5) 健康指数计算:分别计算各待评估轴系的所有样本对“良好轴系类”的隶属度均值,利用式(13)计算得到各轴系的健康指数,以此评估轴系健康状态。
2.2.3 健康指数的有效性评价
FCM聚类模型是轴系健康指数计算的关键工具,该模型的聚类效果在很大程度上决定了健康指数的有效性。文献[15]提出了划分系数(P)以评价模糊聚类的效果,取值范围为[1/c,1],该系数越接近于1,说明聚类效果越好,其定义式为
(14)
其中:N为输入样本的数目;c为聚类类别数;μik为第k个样本对第i类的隶属度。
在健康指数计算中,c=2,即P∈[0.5,1],在此定义当P∈[0.8,1]时,计算所得的健康指数有效。
3 应用实例
由于FCM聚类是一种分类算法,被分析样本需包含差异明显的样本以实现分类,笔者提出的基于FCM的轴系健康评估方法的被分析样本中需包含优良和故障两类典型样本,且评估结果准确度受典型样本数目影响。为此,对状态优良和具有内圈与滚珠耦合故障的两类轴系分别采集了30组振动信号,并对4个待评估正常轴系分别采集了5组振动信号。
3.1 试验设备及设置
为获取轴系性能评估所需数据,采用图1所示振动测试装置对优良、故障及正常工作的3类轴系开展振动测试。驱动控制设备及功率电源分别控制和驱动电机带动轴承组件按设定转速转动,定义轴承组件径向为x向和y向,轴线方向为z向,采用振动测试设备和安装在主轴上端的三轴加速度传感器采集振动信号。设置采样频率为25.6 kHz,测试转速分别为300,3 000及4 600 r/min,每组采集时间为1 s。

图1 振动测试装置及传感器安装图Fig.1 Vibration test rig and position of accelerometer
3.2 试验结果及分析
对优良、故障及正常轴系共80组振动实测信号进行共振解调,获得包络频谱。采用式(8)~式(12)提取各组振动信号的峭度和特征谱线明显度并归一化处理,以此为输入,采用FCM聚类模型获得4个正常工作轴系对优良轴系类的隶属度,通过式(13)、式(14)分别计算健康指数和划分系数。
3.2.1 健康指数分析
图2给出了不同转速下样本健康指数分布图,横坐标为样本编号,纵坐标为健康指数。从图中可以看出,300 r/min转速下优良轴系、故障轴系及待评估轴系的样本健康指数分布离散且无明显区分;而3 000 r/min和4 600 r/min转速下,优良轴系和故障轴系的样本健康指数分别集中分布于1和0附近,各待评估轴系的样本健康指数分布相对集中且差异明显。上述现象的原因在于缺陷引起的振动特征在高转速下比在低转速下更易被激发,而不同健康状态轴系的振动特征存在差异,从而高转速下更易区分不同健康状态轴系。
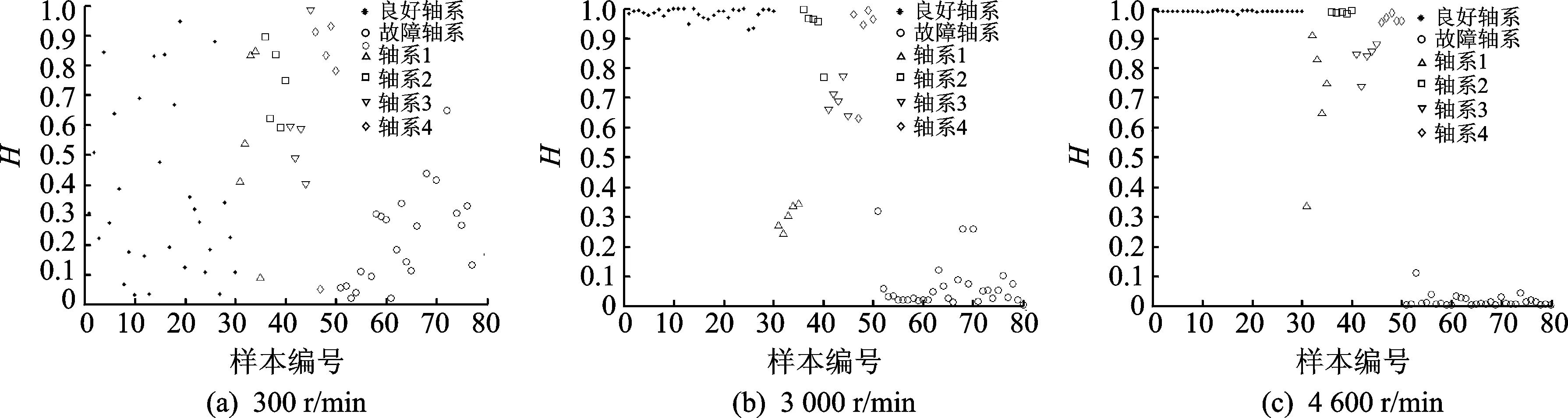
图2 不同转速下的样本健康指数分布图Fig.2 Distribution maps of the samples’ health index at different rotation speeds
从图2(b)和图2(c)中待评估轴系的健康指数分布分散程度可以看出,轴系健康指数越小,样本健康指数分布越分散。分析该现象的原因是,轴系健康状态越差,其运转状态越不稳定,体现为振动特征不稳定。上述现象也表明,为提高评估结果的可信度,需增加输入样本数目,以健康指数的均值作为最终评估结果。比较图2中不同转速下各轴系的健康指数分布范围,可以看出不同转速下健康指数存在差异,对于健康状态较差的轴系1,差异尤为明显。这是因为在不同转速下缺陷引起的振动特征存在差异,且在特定的转速下最为显著。
表1给出了不同转速下各轴系的健康指数取均值后的结果。从表中评估结果可以看出,3种转速下各轴系的健康指数排序一致,均为轴系2健康指数最大,轴系4次之,轴系1最小,与实际情况一致。这说明该轴系健康评估方法可按照健康状态对轴系正确排序,可应用于空间轴系的筛选,而且在3 000和4 600 r/min转速下, 各轴系的健康指数差异显著,评估结果基本一致。这说明该轴系健康评估方法在较高转速下可给出可靠的健康指数,为空间轴系的性能评级提供了可行的途径。
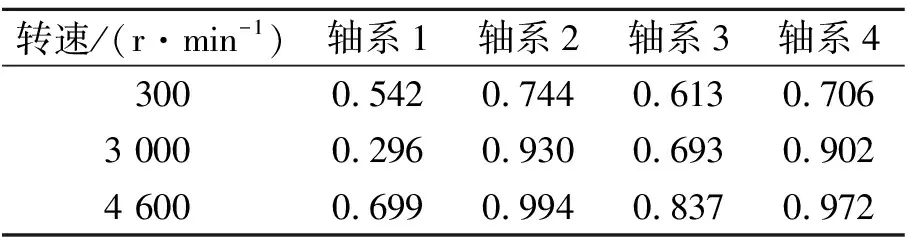
表1 不同转速下各个轴系的健康指数
3.2.2 评估有效性分析
表2给出了不同转速下聚类模型的划分系数。从表中数据可以看出:3 000和4 600 r/min转速下划分系数均大于0.8,评估结果有效;而300 r/min转速下虽实现了正确的健康状态排序,但由于该转速下划分系数小于0.8,聚类效果不佳,该转速下得到的健康指数无效。根据上述结果并结合实际分析,该轴系健康评估方法在转速大于3 000 r/min时,健康评估结果相对可靠。

表2 不同转速下聚类模型的划分系数
4 结束语
鉴于现有轴承健康状态评估方法在空间机构轴系上的应用存在难度,提出了一种基于模糊C-均值聚类的空间机构轴系健康状态评估方法,避免了获取轴系全寿命周期测试数据时间长、成本高的难题。该方法定义的特征谱线明显度可有效敏感轴系健康状态差异,构造的健康指数可量化评估轴系健康状态。应用实例表明,该方法不仅可对轴系健康状态正确排序,且在高转速下可给出相对可靠的健康指数,验证了该方法的可行性和有效性。笔者提出的健康评估方法为目前亟待解决的空间精密轴系的筛选和性能评级提供了可行途径。
参 考 文 献
[1] 王虹, 卿涛, 周刚, 等. 预载对飞轮用轴承组件振动特性的影响研究[J]. 空间控制技术与应用, 2015, 41(1):41-45.
Wang Hong, Qing Tao, Zhou Gang, et al. Effects of preload on the micro-vibration properties of bearing assemblies in fly-wheels [J]. Aerospace Control and Application, 2015, 41(1):41-45.(in Chinese)
[2] 卿涛, 周刚, 张激扬, 等. 空间惯性执行机构精密轴系的长寿命润滑技术[C]∥航天器高精度长寿命执行机构技术发展研讨会论文集. 北京:总装备部卫星系统技术专业组,2012:1-14.
[3] Yu Jianbo. Bearing performance degradation assessment using locality preserving projections [J]. Expert Systems with Applications, 2011, 38:7440-7450.
[4] 张建宇, 张随征, 管磊, 等. 基于多小波包样本熵的轴承损伤程度识别方法[J]. 振动、测试与诊断,2015,35(1):128-132.
Zhang Jianyu, Zhang Suizheng, Guan Lei, et al. Pattern recognition of bearing defect severity based on multiwavelet packet sample entropy method[J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(1):128-132.(in Chinese)
[5] Jiang Huiming, Chen Jin, Dong Guangming. Hidden Markov model and nuisance attribute projection based bearing performance degradation assessment[J]. Mechanical Systems and Signal Processing, 2016,72-73:184-205.
[6] Li Feng, Chyu M K, Wang Jiaxu, et al. Life grade recognition of rotating machinery based on supervised orthogonal linear local tangent space alignment and optimal supervised fuzzy C-means clustering[J]. Measurement, 2015,73:384-400.
[7] Pan Yuna, Chen Jin, Li Xinglin. Bearing performance degradation assessment based on lifting wavelet packet decomposition and fuzzy c-means [J]. Mechanical Systems and Signal Processing, 2010, 24:559-566.
[8] 潘玉娜, 陈进, 李兴林. 基于模糊C-均值的设备性能退化评估方法[J]. 上海交通大学学报, 2009, 43(11):1794-1797.
Pan Yuna, Chen Jin, Li Xinglin. Fuzzy C-means based equipment performance degeneration assessment[J]. Journal of Shanghai Jiao Tong University, 2009, 43
(11):1794-1797.(in Chinese)
[9] 吴军, 郝刚, 邓超, 等.基于模糊C-均值聚类的轴承性能衰退评估方法[J]. 计算机集成制造系统, 2015,21(4):1046-1050.
Wu Jun, Hao Gang, Deng Chao, et al. Novel bearing performance evaluation method based on fuzzy C-means clustering algorithm[J]. Computer Integrated Manufacturing Systems, 2015, 21(4): 1046-1050.(in Chinese)
[10] 周建民, 徐清瑶, 张龙, 等.基于小波包Tsallis熵和FCM的滚动轴承性能退化评估[J]. 机械传动, 2016,40(5):110-115.
Zhou Jianmin, Xu Qingyao, Zhang Long, et al. Rolling bearing performance degeneration assessment based on the wavelet packet Tsallis entropy and FCM[J]. Mechanical Drive, 2016,40(5):110-115.(in Chinese)
[11] Esme E, Karlik B. Fuzzy c-means based support vector machines classifier for perfume recognition[J]. Applied Soft Computing, 2016,46:452-458.
[12] Kesemen O, Tezelö, özkul E. Fuzzy c-means clustering algorithm for directional data (FCM4DD)[J]. Expert Systems with Applications, 2016,58:76-82.
[13] 刘瑞扬, 王毓民. 铁路货车滚动轴承早期故障轨边声学诊断系统(TADS)原理及应用[M]. 北京:中国铁道出版社,2005:30-31,40-41.
[14] 梅宏斌. 滚动轴承振动监测与诊断[M]. 北京:机械工业出版社,1995:12-13.
[15] Bezdek J C. Cluster validity with fuzzy sets[J]. Cybernet,1974,3:58-73.
