单元复习课的教学思考——以浙教版七年级上册第四章《代数式》为例

☉浙江省宁波市奉化区松岙中学 傅前达

2017年11月，浙江省宁波市奉化区举行名师高级研修班优质课堂教学展示活动，笔者有幸执教浙教版第四章《代数式》单元复习课，从备课到实施教学与课后反思，对单元复习课教学进行了深入思考，现将本课的教学实录与课后反思与各位同行分享.

一、教学过程实录

环节1：阅读概念，培养习惯

师：（出示课本代数式的概念图片）同学们，在代数式这个概念中，“运算”指的是哪些运算？

生1：运算指的是加法、减法、乘法、除法、乘方、开方，它们对应的符号分别是+、-、×、÷、（ ）n，

师：很好！复习时，我们要阅读课本，逐字逐句理解概念的含义.现在，老师从你们平时的作业中收集到一些代数式，你们觉得哪些代数式书写不够规范？

生2：a5应写成5a，数和字母相乘时，数一般写在字母的前面！

生3：x2-1x+1应写成x2-x+1.数和字母相乘时，当数为1或-1时，1一般省略不写！

师：我们不仅要会写代数式，而且要规范表达代数式！

教学说明：本教学片断从本章的核心词“代数式”这个概念出发，通过阅读课本概念提出问题，帮助学生养成阅读课本，逐字逐句理解概念的习惯，随后的代数式书写规范“找茬”环节帮助学生养成规范表达的习惯.

环节2：建构知识体系，落实基础

师：现在你们能给黑板上所写的式子分类吗？

师：你能用图示说明代数式、整式、单项式、多项式的关系吗？

生9：我想到了用维恩图表示它们的关系，如图1.

图1

师：到目前为止，我们学习了代数式中的整式，以后我们还会认识更多类别的代数式！现在，你能说出以上单项式的系数和次数，多项式的次数吗？

（学生一一作出回答，师生共同回顾单项式和多项式的次数概念，然后做以下练习）

练习1：请你利用代数式2，x3，y2构造单项式和多项式，说出单项式和多项式的次数.

练习2：按规律排列的多项式-a10+3a9b-5a8b2+7a7b3-9a6b4+…的第10项是______.

教学说明：本教学片断让学生根据现有的代数式进行分类，梳理代数式相关概念间的关系，建立知识体系，通过回忆单项式和多项式的次数等概念落实基础.后续的两道练习题从单项式次数和系数的角度进一步落实概念.

环节3：通过运算，感受代数思想

教师出示以下题目，学生先尝试自己做，教师投影展示学生的解题过程：

学生展示过程如下：

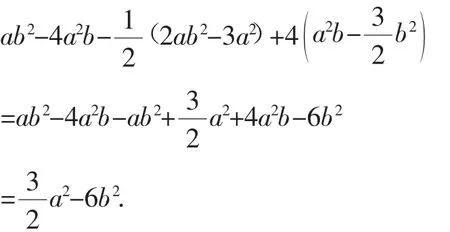
师：运算正确，书写也非常规范！你能说出每一步运算的依据吗？

生10：先去括号，再合并同类项，最后代入求值.

师：运算要步步有据.我们继续思考这样一个问题：上题中把条件“a=-2，b=3”改为“a2-4b2=4”，能求出代数式的值吗？（学生思考）

生11：当a2-4b2=4时，可以假设a=0，则b2=-1，噢，b2为负数了，不行！假设b=0，则a=±2，再把a，b代入代数式求值，结果为6.

生12：我取的值是a2=16，b2=3，计算的结果也是6！

师：那么，我们是不是需要把所有符合a2-4b2=4的值全取遍呢？

当a=-2，b=3时，

师：很好！满足的a2-4b2=4的a,b的值有无数对，我们无法用所有的数对去验证这个代数式的值是不是都等于6，但是我们运用整体思想，整体代入求值，这个代数式的值就确定了！非常妙！请同学们运用这种整体的思想完成以下练习.

练习：当x=1时，代数式px3+qx+1的值为2017，则当x=-1时，代数式px3+qx+1的值为______.（学生自主计算再展示交流）

教学说明：本教学片断设置了一个本单元中的代数式的求值问题，从直接代入求值到整体代入求值，让学生初步感受代数思想，体悟整体思想.值得一提的是，这里呈现了七年级学生最容易犯的错误：寻找具体的数值代替字母求值.通过这道题潜移默化地培养学生严谨思维的习惯.

环节4：解决问题，进一步深化代数思想

教师出示下题：如图2，大长方形的长为60cm，它被分割为7小块，除阴影A、B外，其余5块是形状大小完全相同的小长方形，其中小长方形的较短一边长度为10cm.设阴影A和B的面积之和为S（cm2），阴影A和B的周长之和为C（cm）.

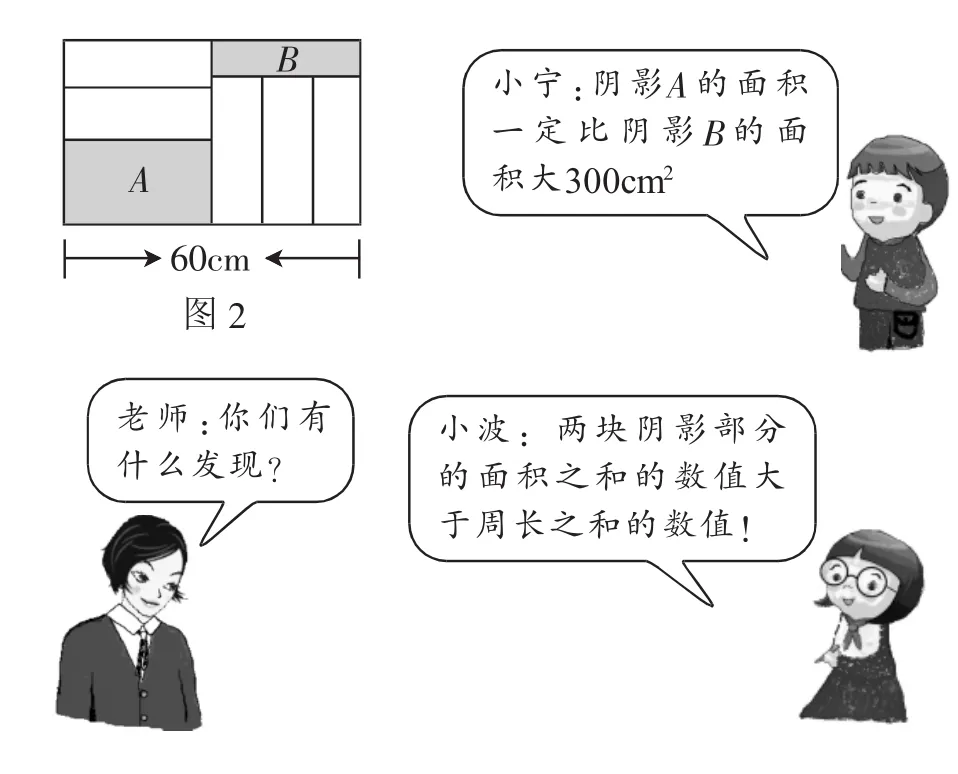
请问小宁和小波的说法正确吗？并说明理由.

（学生充分思考、讨论交流）

师：小宁说的到底对不对？

生14：我假设大长形的宽为40，则阴影A的长为30，宽为20，阴影B的长为30，宽为10，面积之差确实为300！

师：刚才生14假设大长方形的宽为40，结果恰为300，那么如果宽变为其他数据，结果一定还是300吗？如果是，你有没有办法说明所有情况都是300？

生15：如图3，我假设大长方形的宽为x，则阴影A的长为30，宽为x-20，阴影B的长为30，宽为x-30，则SA=30（x-20）=30x-600，SB=30（x-30）=30x-900，

所以 SA-SB=（30x-600）-（30x-900）=30x-600-30x+900=300.

图3

所以小宁的说法是正确的.

师：太棒了！想到用字母x表示大长方形的宽，这样就能表示阴影A，B的面积，这样我们就说明了宽无论如何变化，阴影A，B的面积差都是300！

生16：（迫不及待地）老师，刚才这么一算，我发现阴影A，B的长是一样的，要算它们的面积之差，其实就是算宽度之差就行了，阴影A的宽是大长方形的宽减去20，阴影B的宽是大长方形的宽减去30，所以它们相差10，所以面积相差300！原来小宁是这么发现的！

师：太棒了！我们不仅用字母表示来解决了这个问题，还学会根据图形来进行直接分析！好，继续讨论小波的说法是否正确！

生17：因为S=SA+SB=（30x-600）+（30x-900）=60x-1500，

C=CA+CB=2［30+（x-20）］+2［30+（x-30）］

=60+2x-40+60+2x-60

=4x+20，

所以S-C=（60x-1500）-（4x+20）=56x-1520.

师：它们的差和刚才不一样，算出来就是常数300，这里是一个代数式56x-1520.

生18：它们的大小和x的取值有关！

所以小波的说法也是正确的.

（全班自发地响起掌声）

师：非常精彩！从图中挖掘隐含条件解决问题，这就是数学的魅力！最后，老师想让你们继续用数学工具解开一个神秘的问题：用你的QQ号猜测你的年龄！

谜题如下：

1.获取你的QQ号码的第一位；

2.用你QQ号码的第一位乘以5；

3.把这个数加上8；

4.把所得的结果乘以20；

5.把所得的结果加上1858；

6.把所得结果减去你的出生年份；

7.现在你得到的这个数的后两位就是你的年龄.

（学生运用代数式揭开谜底）

教学说明：本教学片断设置了一个对话形式呈现的判断题，激起了学生强烈的讨论欲望，从特殊值到想到用“字母代替长方形的宽”正是代数思想的体现，通过问题解决进一步让学生感受本章内容的核心：字母代替数的意义.最后用QQ号算年龄更是激起了学生的探索欲望，进一步感受“字母代替数”的价值，帮助学生形成代数思想.

环节5：回顾思考，总结提升

回顾本章内容的知识体系，尝试用结构图表示，回顾本节课印象最深的问题，归纳所涉及的数学思想方法，进一步感悟代数思想.

师：好像很有道理！

二、教学反思

本节课以浙教版七年级上册第四章《代数式》为例，研讨如何上好单元复习课，在实践和研讨的基础上，笔者形成以下观点，和各位同行交流：

1.紧扣单元复习目标，着力单元核心思想

笔者认为，单元复习有别于期中期末和中考复习，单元复习重在以本单元的内容为核心，梳理并建构本单元的知识体系，感悟和理解本单元的核心思想，适当增加本单元和其他内容之间的关系.如本课例所涉及的第四章《代数式》复习，不仅要让学生掌握基础知识，更应通过具体的问题解决让学生进一步体悟代数思想，体会“用字母表示数”这个工具来解决问题的一般性、便捷性、不可替代性.因此，设计单元复习课教学，首先要提炼单元核心思想，围绕核心思想设计层层递进的问题，力求通过问题让学生经历问题解决的过程，感悟内容所蕴含的思想方法.

2.建构单元知识体系，梳理夯实基础知识

在一个单元中，知识往往是按照一定的体系逐步展开的，零碎地散落在学生的头脑中，很容易遗忘，单元复习教学的目的，需要把这些“散落的珍珠”串成“线”，以一定的组织有序地存储在学生的头脑中.所以，单元复习课不能缺少“梳理”环节，通过梳理建构知识体系.如本课教学中，引导学生用维恩图建立了代数式、整式、单项式、多项式之间的关系，并通过具体的代数式复习单项式的系数和次数的概念、多项式的次数概念，用平时较少的问题（如找规律问题）让学生观察系数和次数的变化规律，夯实基础知识.基础知识的复习可以用练习强化，也可以用学生平时的错题资源，让学生通过找错、析错、纠错来达到反省的目的.

3.重视学习现实，培养学习习惯

总结、回顾、反省、归纳是数学学习的重要方法，单元复习应起着这样的功能：通过一个单元的复习，养成良好的数学学习习惯，通过长此以往的行动与坚持，内化为学生自身的一种素养.笔者认为，单元复习是将书从厚读到薄的过程：学生通过阅读课本的概念，进一步理解概念的关键字词，并将概念的本质内容了然于心，通过翻看自己平时的作业梳理解题注意事项，通过综合性问题的解决感悟单元内容的核心.如本课教学中，有意让学生通过阅读课本代数式的概念培养学生如何自主阅读概念，有意通过学生平时作业的纠错提醒学生注意解题规范，在代数式的求值运算中让学生暴露错误并深刻感悟代数思想.培养学习习惯需要从学习之初抓起并坚持不懈努力，需要教师关注学生现实，根据不同学生实际情况，通过示范、展示、交流等方式来帮助学生形成良好的学习习惯.H