重构教学素材 培养学生自我监控能力——以“圆周角定理”教学片断为例

☉山东省滨州市北镇中学初中部 孙长智

章建跃博士在《数学教育心理学》一书中特别提到：“调查表明，学生只会做‘结构良好’的题目，以获得问题的答案为最后目标，不习惯于数学学习的反思和调节的情况非常严重.这是导致数学学习效率低下的重要原因，因此，培养学生数学学习的自我监控能力具有很大的现实意义.”那么教师在教学中，如何来培养学生的自我监控能力呢？笔者在日常教学中，尝试挖掘教学素材的“自我监控”功能，通过重构内联、激思促变，来培养学生学习中的自我监控能力.现举一教学案例说明，恳请各位同行批评指正！

一、对“自我监控能力”的理解

自我监控能力，顾名思义就是指在学习过程中，学生对自己思维过程的自我监控和调节能力，在思维活动上表现出精确性、概括性、深刻性、批判性等鲜明特征.自我监控能力体现在诸如问题方案的酝酿和优化，解题方法的斟酌选择，对问题答案的猜想和寻证，学习节奏的把握，错误原因的查找，反思总结经验教训，以及客观评价学习效果等多样的学习活动中.具备一定的自我监控能力是学生思维能力发展到较高层次，以及具有较成熟的学习能力和独立解决问题能力的重要标志，而“提高学生的思维检验和反思技能是培养学生自我监控能力的有效途径”.

二、案例简录及评析

案例内容来自人教版初中数学九年级上册“24.1.4圆周角”一节.根据教学需要，笔者对教材内容作了大幅度的改编加工，后经上课实践，又对局部内容加以调整，才有此案例.

1.找相关位置，“监控”背景优化

（在学习圆周角的定义后）

问题1：在一个圆中，可以作出无数个圆心角和圆周角，那么一个圆心角和一个圆周角之间可能存在着什么样的关联呢？先独立画图探究，之后小组交流.

（教师收集学生的各类画图并用多媒体分类展示）

展示1：圆心角与圆周角没有关系的情况举例.如图1（1）～（4）等.

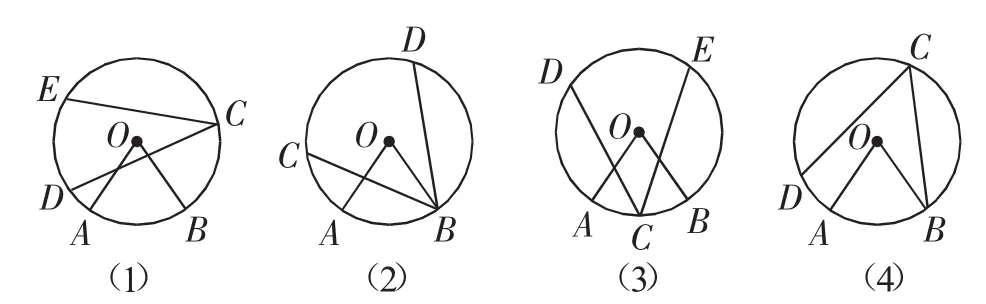
图1

展示2：圆心角与圆周角有关联位置举例.如图2（1）～（4）.

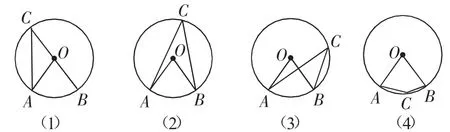
图2

师：哪位同学能讲一讲你的探究过程？

生1：“相关”就是有关系，一开始并不清楚，先画图，画出一些圆心角和圆周角，然后对照去想是否有关系？经过多次尝试，我找出了图2（2）、（3）两个相关图形.

生2：我是采用“一静一动”方式来对比的，先画一个不变的圆心角，另一个圆周角是动态的，位置变，大小也可变，试图与圆心角建立联系.图2中的（1）～（4）我都找到了.

师：多数同学也是经历了“画图寻求，自我监控，多次调整”这样一个过程.图1中所列位置，怎么理解“没有关系”？

生3：因为它们不相关，一个角在变化（位置改变或大小改变），对另一个角没有影响.

师：那图2中所列情况，又如何认识其相关性呢？

生4：若A点（或B点）运动，两角大小随之变化.

生5：我承认点A或B运动时，两角大小同时改变.但若是C点在圆周上运动，会发现与∠AOB无关啊？

生6：难道你没发现图2（1）～（3）中∠ACB都是相等的吗？也就是说，尽管∠ACB的位置变了，但是∠AOB与∠ACB的大小都没变.

（一石激起千层浪，学生议论纷纷，部分学生重新去画图、测量验证）

生7：（补充）图2中的圆都是等圆.图2（1）～（4）等同于“同一圆中C点在圆周上不同位置∠ACB的呈现”.

师追问：图2（4）中当点C在劣弧A（B上运动时，∠ACB的大小也不变吗？

众生：（画图测量后）是这样.

师：问题1要求找出圆心角和圆周角之间的关系，你们的想法是什么？

生8：先找到圆心角与圆周角相关联的位置，再探究它们之间的数量关系.

问题2：谁能总结出这两类相关角的位置特征呢？生9：圆心角和圆周角两边的交点都在圆上.

评析：本环节教材上采用“单刀直入”的方式，直接出示问题：“研究同弧所对的圆心角与圆周角之间的关系.”现在将这种“确定”的问题变为开放性问题：“同圆中的一个圆心角和一个圆周角之间可能存在着什么样的关联呢？”问题被置于一个大的背景下，学生有作图尝试、有筛选对比、有交流反思，思维的活跃融汇着自我监控和自我调整，这是学生自我监控活动的“初体验”.以找相关位置作为突破口，推进“作图”和“讲理”的有效展开，目的是引导学生从复杂、模糊的问题背景中抽身出来，开辟出一条清晰的思考路径，这是任何“现成问题”所没有的效果.在创设的教学情境中，教师适时调控，引导学生开展甄别、猜想及讲道理等实践活动，让学生逐渐对自己的思维活动产生自我监控的意识.

2.找特殊位置，“监控”目标设定

问题3：我们找到了“相关的位置”（如图2（1）～（4）），接下来要去做什么？又准备从哪儿入手呢？

几生：求证数量关系，从图2（1）入手.

生10：（补充）从特殊位置入手，如图2（1），圆周角的一边恰好过圆心，就是特殊位置.

师：为什么要找特殊位置？你认为哪类位置可称得上是特殊位置呢？

生11：特殊位置相比一般位置信息多，更容易发现规律.

师：找特殊点、画特殊图形、取特殊位置确实是在解决问题中常见的先行获取信息的捷径.

生12举手：还有一处特殊位置，如图3，结构上与图2（1）一样.

师：很好！既然是特殊位置，发现什么规律了？

生13：∠AOB=2∠ACB，图3结论也一样.

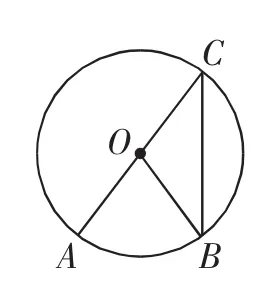
图3

问题4：我们在特殊位置下发现了圆心角与圆周角的数量关系，推而广之，大家对一般位置下的圆心角与圆周角数量关系的猜想是什么？

评析：为什么会有自我监控现象发生？订立计划和执行计划是学生自我监控活动的主要依凭，计划的导向作用会左右着人的思维走向.找特殊位置环节，就是订立计划的一部分，这一问题，让学生自我监控的心理活动加剧，“研究问题为什么往往从特殊情况入手？”“特殊位置在哪里？”“特殊位置下的结论是什么？”本环节的教学处理上，尽力拉长学生的思维链条，让学生舒展想法，凸显出学生自我监控和自我认识深化的过程.思考后知道，之所以称为特殊位置，是因为比一般位置包含有更多的信息，能让我们未“做”先“知”，提前走出朦胧阶段，尽早形成解决问题计划的雏形.而当从“特殊”再回到“一般”时，学生自然而然的对问题的整体认知程度会升级，探究计划也会在酝酿中趋于完善.

3.找转化位置，“监控”问题关联

问题5：现在大家获得了猜想∠AOB=2∠ACB，那么一般情况图2（2）和图2（3）下一步该如何求证呢？

（学生思考、讨论）

几生：我认为应该和特殊位置图2（1）建立联系.

师：你们怎么有这种想法？

生14：以前好多问题都是这样考虑的，由特殊获得一些认识，再推广到一般，然后又利用特殊去求证.

师：好！那现在考虑如何与特殊情况的图2（1）建立联系？

生15：只能新造一条辅助“直径边”，如图4，过C点作直径CD，这样图4（1）、（2）就各包含有两个图2（1）的基本图形.

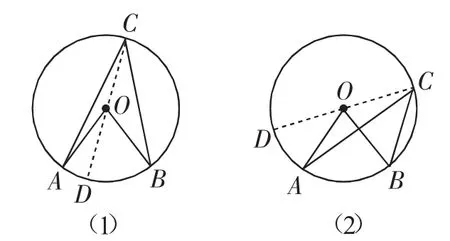
图4

师：请写出证明过程（.稍等）还有问题吗？

师：找找看是哪些基本图形？（生答出）然后呢？

几生：图2（4）还没说明关系.

生17：与图4（1）一样！圆周角是∠ACB，而圆心角是大于180°的∠AOB，辅助线作法、推证思路、结论均与图4（1）一样.

评析：解决问题靠转化，而转化的路径和依据是教师引领的着力点，本环节教学素材是按这两方面来重构的，以加强“通识通法”的教学，目的是让学生自我监控的触角伸的更远、更有力量.怎样将一般情况（指圆心在圆周角内部或外部时的情况）转化为圆周角有一条“直径边”的特殊情况？从“特殊”到“一般”，又回到“特殊”，这条路径上到底发生了什么？学生循问题方向而动，自我监控的指向性和力度渐渐增强，对特殊（基本）图形在解题中的作用印象深刻，同时见证了图形的分解、组合这一解题策略的优越性.

4.找归纳位置，“监控”定理延展

问题6：相关位置下的圆心角和圆周角的数量关系已经得出，想一想怎么总结？

生18：如果一个圆心角和一个圆周角两边的交点都在圆上，那么圆周角的度数是圆心角度数的一半.

师：仅看交点，如图2（4）对应关系不够明确！

生19：既然两个角的两边的交点都在圆上，意味着这两个角对着同一条弧，可以说成“一条弧所对的圆周角等于它所对的圆心角的一半”.

众生：这样表达简洁且清楚！

生20：这种说法还有一好处就是将圆周角和弧联系起来了.前面学习垂径定理，弧、弦、圆心角关系定理等，都有同弧或等弧的说法.

问题7：如果我们的视野再放开一点，将刚学的“圆周角定理”与前面所学圆的知识做一关联性的衔接，你有什么发现呢？

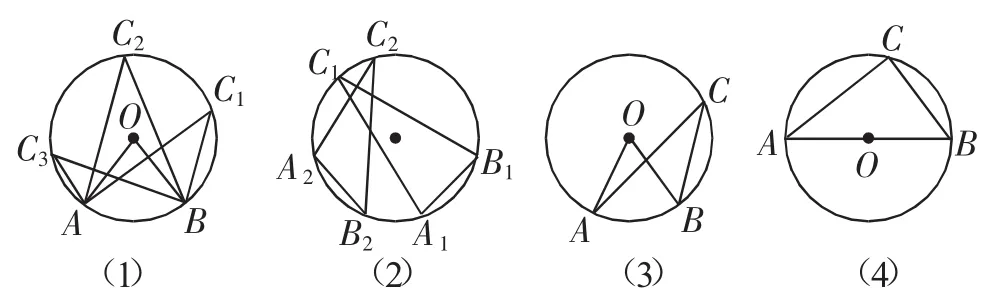
图5

整理后得到：

（1）同弧所对的圆周角相等.如图5（1）中，∠C1=∠C2=∠C3等.

（2）在同圆中，等弧所对的圆周角相等；在同圆中，相等的圆周角所对的弧相等，所对的弦相等.如图5（2）中，若=，则∠C1=∠C2；若∠C1=∠C2，则=，A1B1=A2B2.

（3）在等圆中，相等的圆周角所对的弧相等.如图5（2）、（3）中，∠C=∠，则=（.讨论：为什么强调在“等圆”中？）

（4）直径所对的圆周角是直角；90°的圆周角所对的弦是直径，如图5（4）所示.

师：请一名同学谈谈自己归纳新命题的心路历程.

生21：学的这些定理中，以相同的量为桥梁，可沟通彼此，比如圆心角，弧、弦与圆心角有联系，而圆心角与圆周角也有联系.还有同弧与等弧，同圆与等圆，劣弧、优弧与半圆等都可以类比推广开来.

评析：本环节改变教材单一的定理总结，改为随机性的真命题归纳，这对学生的知识基础、归纳分析能力是一个大的考验.各定理杂糅，同弧与等弧，同圆与等圆，劣弧（或优弧）与半圆等，归纳位置多元，同时涉及到圆弧、弦、圆心角、圆周角等多种“圆量”，可谓林林总总.通过反思和归纳，学生对各命题之间关系的敏感性增强，使知识联系宽泛而有序，方法使用灵活而多样，并孕育了知识结构系统.归纳的过程伴随着对比、质疑、调整、优化等自我监控活动，同时新知识系统的构建为学生自我监控质量的提高做了知识和方法上的储备.

5.找变式位置，“监控”应用变通

问题8：填空：

（1）如图6（1）所示，C点是⊙O内一点，且∠AOB、∠ACB在弦AB所在直线的同侧，则∠AOB______∠ACB；

（2）如图6（2）所示，C点是⊙O外一点，且∠AOB、∠ACB在弦AB所在直线的同侧，则∠AOB______∠ACB（.填“＞、＜或=”）

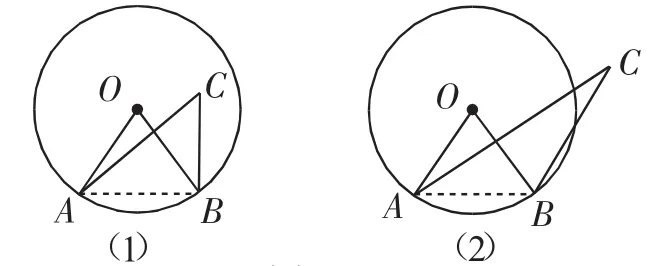
图 6

生24：图7（1）中，延长AC与⊙O交于C′，连接BC′；图7（2）中，设AC与⊙O交于C′点，连接BC′.

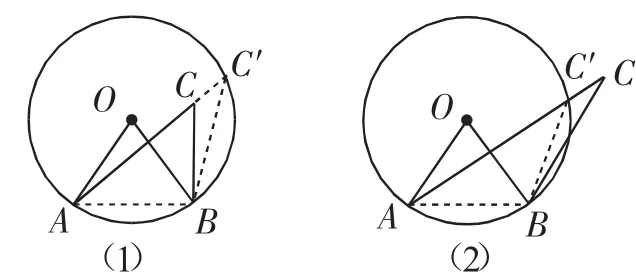
图 7

问题9：如图8，在⊙O中，圆周角∠ACB=30°，弦AB=2，求⊙O的半径.

师：特殊角30°在△ACB中的作用不清楚，弦AB=2好像与半径也联系不上！

生25：如图9（1），可作出A（B所对的圆心角，知∠AOB=60°，得到等边△OAB，则半径OA=AB=2.

生26：我有另一解法，如图9（2），作直径AC′，连接BC′，则∠C=∠C′，这样就把30°条件转移到了Rt△ABC′中，再利用“30°锐角所对的直角边等于斜边的一半”去考虑即可.

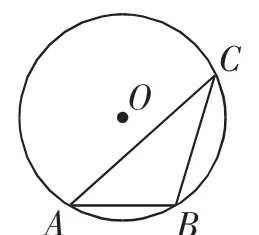
图8

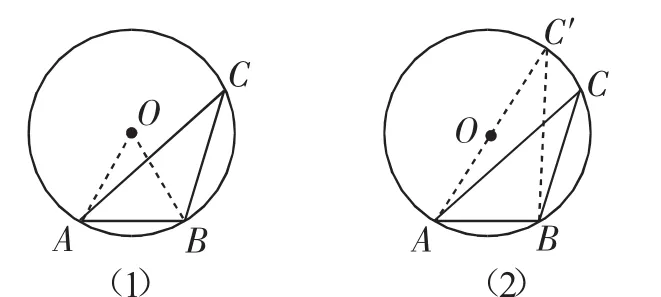
图9

评析：如何实现定理与应用的有效衔接？考虑到新知识初次应用这一实际情况，本环节没有采用教材上综合程度较高的例题来教学，而是围绕同弧所对的圆心角与圆周角的转化关系，设置了两道练习，难度不大，但是需要构图，建立关联，这是学生需要突破的地方.定理“一条弧所对的圆周角等于它所对的圆心角的一半”，传递出了哪些信息？面对题中的“1 2∠AOB”你想到了什么？容易想到构造一个圆周角作为媒介，来联系∠AOB与∠ACB，但紧接着另一个问题出现了，将新构造的圆周角放在哪里合适呢？类似地，问题9中，30°的圆周角如何与半径（或直径）建立联系呢？这些需要跨越的问题提高了学生自我监控的“思维量”，甚至出现胶着状态.随着构图完成，思路明朗，自我监控活动也趋向平缓.

三、几点想法

1.鼓励和引导学生暴露思维过程，为学生自我监控提供凭借

为了使自我监控活动真正发生，需要“刺激源”.这个“刺激源”就是问题本身或者问题引领下的各种想法的展露.本案例通过具体而有挑战性的问题序列（找相关位置、特殊位置、转化位置、归纳位置、变式位置等）激发探究行动，学生在情境中有探究、有想法、有表达，这些“表达”是思维活动的直观呈现.讲给别人听或者听别人讲，都存在一个内心关照或自评价的过程.或者边讲边随机改动最初没有注意到的地方，或者讲完后发现不对又推倒重来，或者讲解中遇到新障碍讲不下去，又或者听完别人评价后加以改动，这些都是自我监控活动的外在表现.我们说，暴露的思维过程是学生自我监控的凭借，是学生自身再提高的起点，更是教师开展教学活动的第一手材料.因此教师在教学中，要千方百计搭设平台，让学生将做法说出来，道理讲出来，过程写下来.

2.要强化反思和检验习惯的养成

学生的自我监控能力实质是由学生的思维发展水平，特别是思维的深刻性、批判性等特征因素决定的.本案例注重学生思维品质的培养，如在背景优化、目标设定、问题关联、定理延展、应用变通等环节，为学生提供了较开阔的思考空间和交流平台，斟酌选择、尝试操作、对比分析、关联优化等思维活动充分而深刻，通过教师点拨和追问，特别强化了反思和检验习惯的养成.需要提出的是，学习过程中，教师要经常提醒学生随时对自己的思维过程进行检验和反思，强化生成，这样久而久之，学生的思维活动就会习惯性的被置于自我监控之下，随着自觉性、主动性等自我意识的增强，学生的学习活动便进入了高一级层次.

3.通过学习形成有价值的“思考结构”，让学生的自我监控“有章可循”

数学是思维的科学，自有一套具有普适性的思考结构和用于交流的符号形式，这种结构和符号形式是强大的，富有逻辑，简明而且精确，是人们可以借助之，用于理解和处理新数学问题的一种思维方式.本案例围绕圆周角定理呈现了清晰地思考结构：筛选出一个圆心角与一个圆周角的各种相关情形（一般）——从特殊位置获取关键信息（特殊）——推广形成猜想（一般）——转化为特殊情形寻证（特殊）——归纳定理（一般）——定理应用（特殊）.这一思考结构和表达方式，将对学生产生积极的现实影响，具有推广价值.教师在问题学习中，要努力帮助学生获得这种有辐射力的“思考结构和符号形式”，以便让学生的自我监控越来越有“章法”.