激光干涉在蜂窝夹心层板振动模态测量中的应用*

陶 楠， 马银行， 姜益军， 杨福俊， 何小元

(东南大学工程力学系 南京，210096)

引 言

作为结构材料需具备良好的刚度、强度、断裂韧性、疲劳强度、吸能、阻尼减振和热稳定性，对于航空及航天结构材料来说，高比刚度比强度是结构设计的重要因素。复合材料的出现，特别是蜂窝夹心复合材料成为满足上述条件的最为合理的结构材料之一[1-2]。因此，蜂窝夹心结构静、动态力学性能的研究与分析成为相关研究的重点和热点之一[3-7]。目前，对于蜂窝夹心结构的研究主要基于有限元方法[8-9]，然而,这些方法大都限于对单独的蜂窝夹层结构运用解析或数值方法分析。对于含有蜂窝夹层板的复杂结构进行分析时，现有的层板单元模型还不能很好地近似蜂窝夹层板。比如将蜂窝夹层板等效成各向同性的薄板,忽略对基频有较大影响的扭转刚度和表层的横向剪切，因此，其近似程度也不好确定[5]。目前，在复合材料静、动态特性的实验研究中，除了传统的单轴拉伸和三点弯曲实验外，还采用测量振动模态方法并结合振动理论来计算复合材料的弹性模量、阻尼因子以及蠕变与断裂等特性[10]。在动态测试方法中用的比较多的是传感器法和激光多普勒法，传感器法需要将传感器直接粘贴在待测结构表面，这样容易改变结构局部的质量分布且只能测得离散的数据，从而影响实验结果的精确性；激光多普勒法是非接触测量，其响应快、测量范围大，不过它是通过快速逐点扫描进行测量，测试精度和速度依赖于测点数。这些测量方法通过傅里叶变换等技术分析采集得到的变形-时间曲线获取结构的振动响应，进而得到结构的模态频率、振型和阻尼特性。上述方法由于是单点测量，很难得到结构振动完整的模态振型，因而无法发现模态跃迁现象。笔者采用有限元法类比分析和光学干涉测量技术的可视性和全场性的优点，对1个完整和2个含不同损伤类型的悬臂蜂窝夹心板的稳态振动特性进行研究，实验结果验证了蜂窝夹心复合材料的横观各向同性，还测得结构前14阶振动模态的振型以及结构损伤引起的模态跃迁现象等。

1 激光干涉测量技术

1.1 离面变形测量光学系统

如图1所示，激光器发出的相干激光经分光镜分为两束光，一束照射到被测物体表面的称为物光，另一束通过光学元件直接进入电荷耦合器件(charge coupled device，简称CCD)相机成像靶面的称为参考光。物光经被测物面漫反射后部分光线进入CCD相机成像靶面，并与参考光干涉形成散斑图像。CCD相机分别采集物体离面变形前、后的散斑图像(分别称为参考图像和目标图像)，计算机软件对采集的两幅图像进行算术减运算可以得到反映物面变形分布的条纹图，条纹图的条纹代表所测物面变形分布的等值线，该方法称为电子散斑干涉技术。对于上述测量方法，如果采集的变形后散斑图像对应的是动态变形，由于CCD相机的光电转换需要一定的时间，因此相机采集到的图像为动态变形对于时间的积分成像，光学计量学把上述过程称为时间平均法。

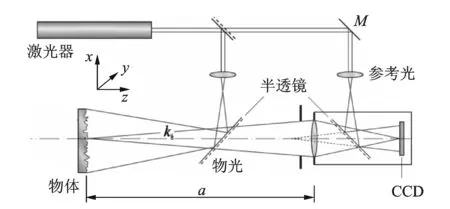
图1 测量离面变形的光学系统Fig.1 Optical setup for measuring out-of-plane deformation

1.2 散斑干涉条纹的形成

对于时间平均法，如物体在初始未发生变形，这时CCD相机记录的散斑光强I0(x,y)为

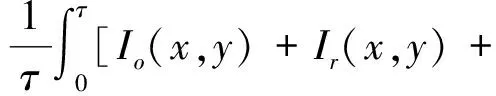
(1)

其中：Io(x,y)，Ir(x,y)分别为相机靶面对应于物面上点(x,y)处物光和参考光的光强；φ(x,y)为试样静止时参考光与物光间的随机相位差；τ为CCD相机图像更新时间。

以上各物理量除了时间t外在物体静止时都是不变的量，因此式(1)可写成

I0(x,y)=Io(x,y)+Ir(x,y)+

(2)

假设物体发生周期性的振动时，CCD相机记录的散斑光强I1(x,y)为

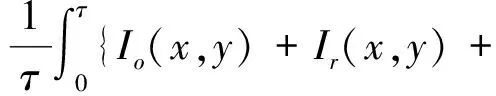
φ(x,y)] }dt

(3)

其中：φ(x,y,t)为物体变形引起的物光相位变化。

对于图1所示的测量纯离面变形系统来说，φ(x,y,t)与物面上点(x,y)处离面位移(变形)之间满足如下的关系[11]

φ(x,y,t)=4πAcos(ωt)/λ

(4)

其中：Acos(ωt)为t时刻物面上点(x,y)处的离面位移；A为离面振动的振幅；ω为振动圆频率；λ为激光波长。

因此，式(3)可改写成

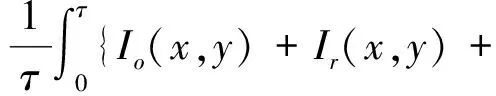
(5)

假设相机曝光时间τ是试样振动周期的整数倍，则式(5)可进一步写成

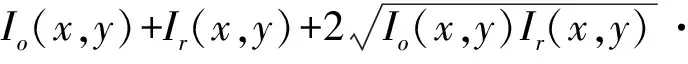
(6)

其中：J0为第1类零阶贝塞尔(Bessel)函数。

零阶贝塞尔函数图像如图2所示。

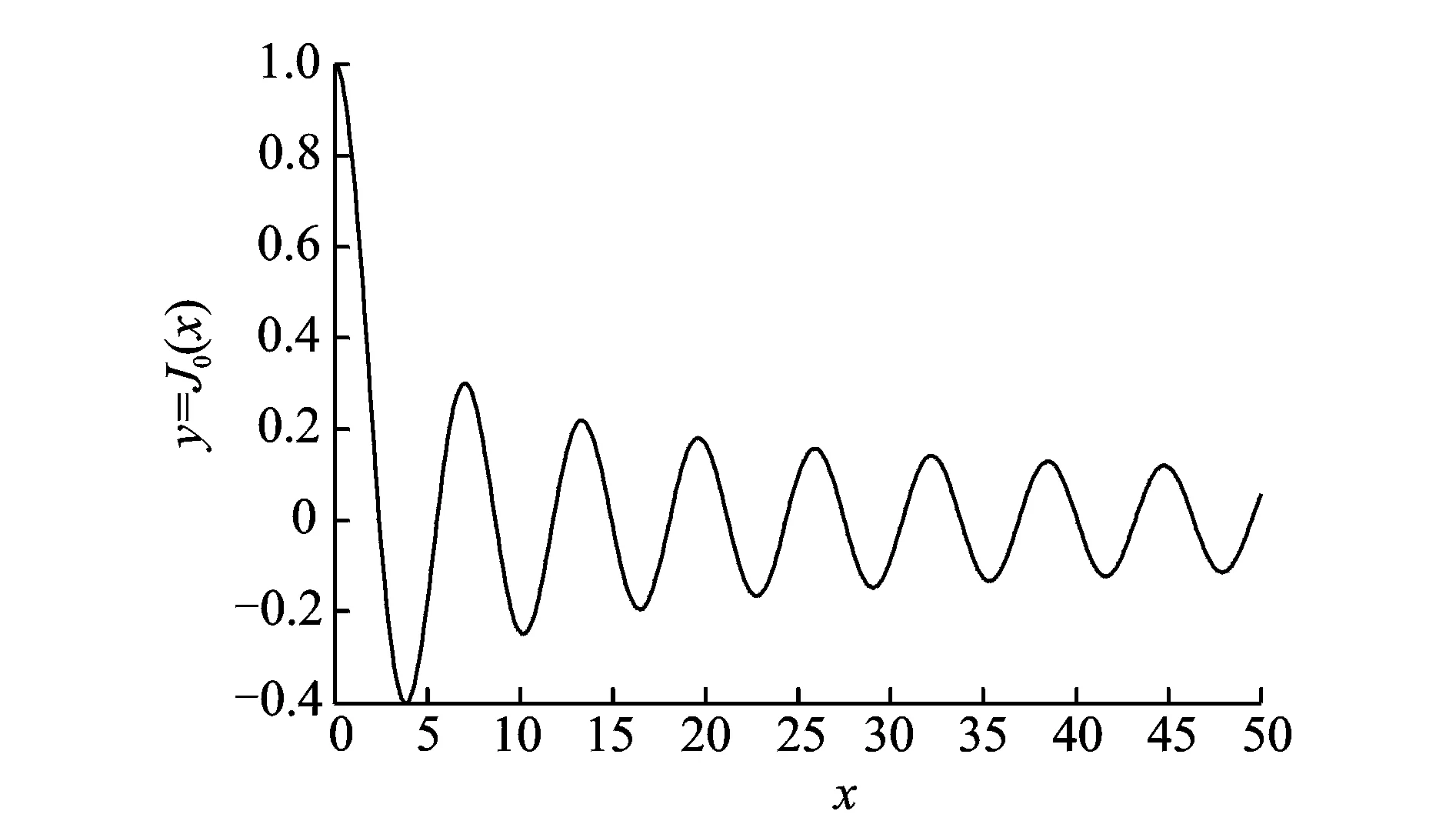
图2 零阶贝塞尔函数Fig.2 First kind zero-order Bessel Function

假设采用文献[12]提出的时间平均法电子散斑图干涉技术，即参考图像并不是试样静止状态下采集的，而是振动状态下的试样图像。考虑振动过程中激振器激励力的振幅微小波动，导致试样振动的振幅从A改变成A+ΔA。若以振幅微小波动情况下的图像为目标图像，则计算机软件对上述两幅图像进行算术减运算后得到的条纹图强度分布[13]为

(4πΔA/λ)2J0(4πA/λ)

(7)

结合式(7)和图2可知，散斑图干涉技术得到的条纹图中最亮的条纹对应于振动节线(驻点线)。

2 有限元模拟类比

对于本实验中使用的蜂窝夹心复合板结构，因进行有限元分析时缺少相应的等效材料参数，为了简单和方便采用有限元方法，模拟计算了长宽尺寸与实验中的测试试样相同的铝板前17阶离面振动的振型云图。悬臂铝板结构有限元模型的物理及几何参数为：弹性模量E=70 GPa；泊松比ν=0.33；密度ρ=2 700 kg/m3；试样大小为145 mm×80 mm×1 mm；边界约束条件为短边夹持固支成悬臂板。有限元计算时选用SHELL 163单元。图3列出的是模拟得到铝板前25阶离面振动的振型云图中与下面介绍的完整蜂窝夹心复合板结构前14阶振型图相同的云图。

图3 有限元模拟得到悬臂矩形铝板的前17阶中14个振型云图Fig.3 Fourteen mode shapes of first 17 resonant mode of cantilever aluminunm plate from FEM simulation

3 实验结果与分析

图4为本实验中使用的蜂窝夹心复合板结构实物图，试样为双层蜂窝夹心复合结构。其几何参数如下：复合板总厚度为9.16 mm；上、下层面板厚为0.80 mm；中间层板(包含树脂层)厚为1.10 mm。上层面板纤维按[0/90/45/135/0/90]进行铺设，中间层板纤维按[45/135/0/90/45/135]铺设，下层面板纤维铺设顺序与上层面板以中间层板为对称。由图4(b)可以看出，两个蜂窝层的蜂窝单元并不是正六边形，其平行对边间的距离在6～7 mm左右。

图4 双夹心蜂窝复合板结构图Fig.4 Structure of double sandwich composite plate viewed from

实验中测试的3个试样如图5(a)，(b)及(c)所示。所有试样尺寸相同，其平面规格及实验时的边界约束和激振点位置如图5(d)所示，试样厚度均为9.16 mm。其中试样2受直径 30 mm 钢球低速冲击碰撞形成损伤，冲击碰撞位置距离试样上端边60 mm，左侧边 40 mm。测量系统中，激光器产生波长为532 nm的绿色相干光，功率0～50 mW连续可调。CCD为德国IDS公司的1 280×1 024像素可编程控制的相机，信号发生器可产生0～20 kHz正弦波，信号发生器产生的正弦信号经功放器放大后输给激振器，试样由激振器的传动杆直接接触其后表面激励。

实验时采用图像相减模式，将输出信号设置为周期性正弦信号，调好信号发生器的输入电压和功率放大器的放大倍数。随着输入频率的改变，计算机上可实时地观测到CCD相机采集到的振动条纹。保持输入电压和功率放大器的放大倍数不变，当输入频率越接近于被测物体的共振频率时，干涉条纹的密集度和清晰度越高，条纹最密时对应的信号发生器产生的谐波频率即为该阶模态的频率。实验时为了提高测试物面的光学反射率，物面需喷上均匀的白色哑光漆，结果如图5(a)，(b)及(c)所示。

实验测得的无损伤试样1前14阶离面振动模态的振型条纹图如图6所示，冲击损伤试样2的振动模态的振型条纹图见图7，图8所示为单层面板断裂试样3前12阶离面振动模态的振型条纹图。

实验测得上述3个蜂窝夹心复合层板试样各阶共振频率值如表1所示，由表1可以看出，由于损伤造成试样结构的局部刚度减小，导致试样2和试样3的各阶共振频率总体低于完整试样1的对应值。若将图6中完整无损试样1的各阶共振振型条纹图与图3中有限元模拟的各向同性材料悬臂铝板的振型云图对比，在考虑激振器顶杆对试样接触点附近区域的附加影响的情况下，发现两者的振型几乎相同(由于试样的材料、厚度与有限元模拟对象间的不同，两者的振型形状不完全是按阶数对应相同的，但总能在有限元模拟的结果中找到与实验结果相同的振型)。因此，大多数学者把蜂窝夹心复合层板看成是横向各向同性假设的观点是可以接受的[14]。

表2是根据图6～图8所示的振动振型条纹图总结出的3个被测试样的各阶振动模式。由表2可知：3个试样的前6阶共振模式相同，但冲击损伤试样2的第7和第8阶模态振型与完整试样1的第7和第8阶振型顺序互换，即结构的局部损伤导致模态跃迁。同样，单层面板断裂试样3的第8和第12阶模态振型与完整试样1的第8和第12阶振动模式也不同，这进一步表明结构的局部损伤导致共振模式的变迁。

图5 测试试样及边界约束与加载设置Fig.5 Geometric dimension and loading configuration of tested plates

图6 无损伤试样1前14阶稳态振动的振型Fig.6 First 14 mode shapes of intact specimen 1

图7 冲击损伤蜂窝板试样2稳态振动的振型条纹图Fig.7 Mode shapes of the specimen damaged by impact load 2

图8 单层面板断裂试样3的稳态振动的振型条纹图Fig.8 Mode shapes of the specimen with cracked front plate 3

表1 测试试样的1～14阶共振频率

表2 测试试样的振动模式

4 结束语

对比有限元模拟和实验测量结果，激光干涉测量技术能够对稳态共振时复合薄板的振动模态进行有效测量。光学干涉测量技术不仅能够获得结构的振动模式，而且还可以分析损伤或缺陷对结构共振模式的影响。本研究除了获得悬臂矩形蜂窝夹心层合板的前14阶离面振动的振型图外，实验结果也表明，由于结构的局部损伤使得局部刚度弱化，将使结构的共振频率减小，其对高阶共振模式的影响也较为明显，比如引起振动模态的跃迁。

参 考 文 献

[1] Gibson R F. A review of recent research on mechanics of multifunctional composite materials and structures[J]. Composite Structures, 2010, 92: 2793-2810.

[2] 杜善义. 先进复合材料与航空航天[J]. 复合材料学报, 2007, 24(1): 1-12.

Du Shanyi. Advanced composite materials and aerospace engineering[J]. Acta Materiae Compositae Sinica, 2007, 24(1): 1-12. (in Chinese)

[3] 徐胜今, 孔宪仁, 王本利, 等. 正交异性蜂窝夹层板动、静力学问题的等效分析方法[J]. 复合材料学报, 2000, 17(3): 92-95.

Xu Shengjin,Kong Xianren, Wang Benli, et al. Method of equivalent analysis for statics and dynamics behavior of orthotropic honeycomb sandwich plates[J]. Acta Materiae Compositae Sinica, 2000, 17(3): 92-95. (in Chinese)

[4] 杨智春, 党晓娟, 王乐, 等. 复合材料结构损伤联合定位法试验研究[J]. 振动、测试与诊断, 2004, 24(2): 115-120.

Yang Zhichun, Dang Xiaojuan, Wang Le, et al. Experimental investigation on a combined damage localization method for composite beams and plates[J]. Journal of Vibration, Measurement & Diagnosis, 2004,24(2): 115-120. (in Chinese)

[5] Yu Shudong, Cleghorn W L. Free fiexural vibration analysis of symmetric honeycomb panels[J]. Journal of Sound and Vibration, 2005, 284: 189-204.

[6] Lasn K, Echtermeyer A T, Klauson A. Comparison of laminate stiffness as measured by three experimental methods[J]. Polymer Testing, 2015,44:143-152.

[7] Treviso A, Van G B, Mundo D. Damping in composite materials: properties and models[J]. Composites Part B, 2015, 78: 144-152.

[8] 唐羽烨, 薛明德. 蜂窝夹芯板的热学与力学特性分析[J]. 复合材料学报, 2005, 22(2): 130-136.

Tang Yuye, Xue Mingde. Thermo-mechanical characteristics analysis of sandwich panel with honeycomb core[J]. Acta Materiae Compositae Sinica, 2005, 22(2): 130-136. (in Chinese)

[9] 张铁亮, 丁运亮, 金海波. 基于有限元法的蜂窝夹层结构稳定性研究[J]. 复合材料学报, 2012, 29(3): 184-190.

Zhang Tieliang, Ding Yunliang, Jin Haibo. Stability problem of honeycomb sandwich structures based on finite element method[J]. Acta Materiae Compositae Sinica, 2012, 29(3): 184-190. (in Chinese)

[10] Gibson R F. Modal vibration response measurements for characterization of composite materials and structures[J]. Composites Science and Technology, 2000, 60: 2769-2780.

[11] Sharpe W N. Handbook of experimental solid mechanics[M]. New York: Springer Science + Business Medial, 2008: 662.

[12] Wang W C, Hwang C H, Lin Shuyu. Vibration measurement by the time-averaged electronic speckle pattern interferometry methods[J]. Applied Optics, 1996, 35(22): 4502-4509.

[13] Ma C C, Huang C H. Experimental and numerical analysis of vibrating cracked plates at resonant frequencies[J]. Experimental Mechanics, 2001, 41(1): 8-18.

[14] Cheng Qianhua, Lee H P, Cheng Lu. A numerical analysis approach for evaluating elastic constants of sandwich structures with various cores[J]. Composite Structures, 2006, 74: 226-236.