压电微操作平台的复合控制*

胡俊峰， 杨明立， 郑昌虎

(江西理工大学机电工程学院 赣州，341000)

引 言

目前，微操作平台在精密加工、微机电系统、生物工程及光学工程等领域应用越来越广泛[1-4]。压电陶瓷驱动器具有响应快、精度高等优点，被广泛应用于微操作领域。但是，压电陶瓷具有迟滞、蠕变和高频振动非线性特性，其中迟滞特性严重降低微操作精度。为了补偿迟滞现象所带来的运动误差，实现微操作平台的快速响应和准确性，需要采用合适的控制策略对其进行运动跟踪。

微操作平台的运动跟踪控制方法主要是前馈控制和反馈控制。前馈控制需要建立压电驱动器的迟滞模型，利用其逆模型进行迟滞补偿消除对微操作平台的影响。用于建立平台迟滞现象的模型主要为Maxwell，Duhem，Preisach及Prandtl-Ishlinskii模型等[5-8]。其中，Preisach是目前应用广泛的模型，具有原理清晰、结构简单、精度高、易于和控制方法相结合等优点[7]。建立精确Preisach模型的关键是建立反映迟滞环的数学表达式，可采用支持向量机理论建立该表达式。但是，难以建立精确描述迟滞现象的逆模型，仅采用前馈控制方法不能满足微操作平台运动控制精度的要求。

反馈控制是利用反馈机制解决迟滞问题，如PID控制、自适应控制、神经网络控制及模糊控制等。刘国华等[9]提出一种联合神经网络和模糊PI控制策略，提高了一种微定位平台的定位精度和响应速度，但BP神经网络在训练过程中存在局部极小值及过学习等问题，特别是样本数较少的情况下，会产生较大的误差。Liaw等[10]设计了一种鲁棒自适应控制器，消除了压电陶瓷的迟滞非线性，具有较强的自适应能力，但缺少前馈，响应速度较慢。所以，需要结合前馈控制与反馈控制的优点设计复合控制器。

为了满足压电微操作平台响应快和稳态精度高的要求，笔者以某一维微操作平台为对象，采用支持向量机建立反映平台迟滞非线性的离散Preisach模型，基于该模型采用迭代搜索法求解其逆模型，提出一种基于该逆模型的前馈补偿同PID反馈调节相结合的复合控制策略。与前馈控制和普通PID控制进行实验验证比较分析，以说明所提出的控制算法的有效性与优越性。

1 建立微操作平台的迟滞模型

1.1 离散Preisach模型

由于压电驱动器的迟滞现象会使微操作平台出现如图1所示的非线性特性，由图1可知，平台的输出位移不仅与当前的输入电压有关，而且与输入电压路径有关，这种现象会影响微操作平台的运动精度。

图1 微操作平台的迟滞非线性Fig.1 Hysteresis nonlinearity of micro-manipulation stage

微操作平台的离散Preisach模型[11]可表示为

(1)

其中：u(k)和g(k)分别为平台在kTs时刻的输入电压和输出位移；Ts为采样周期；αn与βn分别为距离u(k)最近的上升与下降极值点电压；(αi,βi)表示驱动器电压从0上升αi后下降至βi；x(αi,βi)为对应的平台输出位移；f(αi,βi)为驱动器电压从0上升至αi处平台的输出位移与平台从αi下降至βi时输出位移之间的差值。

f(αi,βi)可表示为

f(αi,βi)=x(αi,αi)-x(αi,βi)

(2)

在k-1时刻平台的输出位移为

(3)

联合式(1)和式(3)可得平台在任一时刻的输出位移迭代表达式为

(4)

由式(4)可知，要求出g(k)，需要求出g(k-1)与位移变化量f(u(k),βn))或f(αn,u(k))，可采用支持向量机理论建立位移变化量f(αi,βi)与输入电压(αi,βi)之间非线性关系的回归模型。

1.2 建立支持向量机回归模型

为了采用支持向量机建立反映(αi,βi)与f(αi,βi)之间关系的回归模型，需要合适的样本点，获取样本点的过程如下：

1) 将压电驱动器的最大电压Um等为n分，等分点的电压为jUm/n(j=1,2,…,n)；

2) 将驱动器电压从最小值上升至各jUm/n，然后从该等分点返回至最小值，测量电压在上升和下降阶段各等分点(jUm/n,jUm/n)所对应的位移x(jUm/n,jUm/n)；

3) 对每个等分点重复执行步骤2，可得平台在等分点上的电压(αi,βi)和所对应的位移x(αi,βi)，将其代入式(2)可得f(αi,βi)；

4) 以{[(α1,β1),f(α1,β1)],…,[(αn,βn),f(αn,βn)]}为样本点，n为样本点数。

采用支持向量机建立反映(αi,βi)和f(αi,βi)之间关系的回归模型可表示为

F(z)=ωφ(z)+b

(5)

其中：ω为超平面系数；z为极值点电压(α,β)；b为偏置；φ为低维空间到高维空间的映射；F(z)为f(α,β)。

为了求解式中的ω和b，根据支持向量机回归理论[12]，式(5)转换为如下的优化问题

(6)

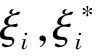
通过引入核函数，式(6)可转化为

(7)

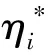
其表达式为

R(z,zi)=exp(-h‖z-zi‖2)

(8)

其中：h为核函数的宽度参数。

式(7)通过序列最小最优化算法[13]求解得到ω

(9)

偏置量b可通过求解二次规划问题得到，采用栅格搜索[14]方法获得参数c和g的最优值

(10)

采用栅格搜索[14]方法获得参数c和g的最优值。

通过式(5)、式(9)和式(10)建立反映微操作平台迟滞的回归函数

f(z) =ωφ(z) +b=

(11)

根据支持向量机所建立的回归模型F(z)可预测任一输入电压(αi,βi)所对应的f(αi,βi)，从而可根据式(4)计算出任一时刻某一输入电压作用下的平台输出位移，即根据离散Preisach模型能求出输 入电压所对应的输出位移。但是，平台的前馈控制的目标在于求得所期望的输出位移所对应的输入电压，即获得离散Preisach逆模型。

2 复合控制器设计

2.1 建立离散Preisach逆模型

由于无法获得离散Preisach逆模型的符号表达式，可以根据式(4)采用迭代搜索方法建立离散Preisach逆模型。建立微操作平台离散Preisach逆模型的思路如图2所示，利用支持向量机回归模型F(z)建立离散Preisach模型，根据该模型采用迭代搜索方法求得平台期望位移所对应的输入电压，即得到平台的离散Preisach逆模型。

图2 建立离散Preisach逆模型的思路Fig.2 Thought for establishing inverse discrete Preisach model

根据所期望位移信号变化情况，需要选择不同的迭代搜索方法。第1种情况是连续变化的位移信号，即位移信号不存在间断点，可采用定步长迭代方法获得其逆模型，算法流程如图3(a)所示。

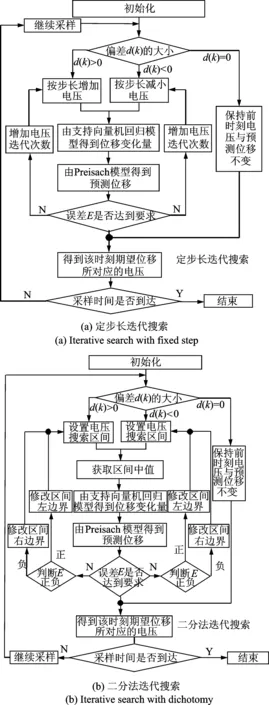
图3 迭代搜索求解Preisach逆模型的算法流程Fig.3 Iterative search algorithm for solving the inverse Preisach model

1) 初始化参数，设定采样时间T、采样周期Ts、平台期望位移r(k)、压电驱动器初始电压α0、电压迭代步长Δα和误差精度E。

2) 由式(4)可知，需要根据目前时刻的期望位移r(k)与前一时刻位移r(k-1)的偏差d(k)选择不同方式进行迭代α(k)。

3) 若d(k)>0，α(k)由α(k-1)按步长Δα迭代增加得到，将(α(k),α(k-1))代入F(z)得到f(α(k),α(k-1))；若d(k)<0，α(k)由α(k-1)按步长Δα迭代减小得到，将(α(k-1),α(k))代入F(z)得到f(α(k-1),α(k))；若d(k)=0，保留前一时刻的α(k-1)与g(k-1)。

4) 由式(4)可计算出α(k)所对应的g(k)，若g(k)与r(k)之间的误差大于等于E，则继续按照步长Δα迭代更新α(k)，直至其误差小于E停止迭代， 则得到的α(k)即为r(k)所对应的输入电压u(k)。

5) 判断采样时间是否达到T，若未到达，返回计算下一目标位移r(k+1)所对应的电压α(k+1)；若到达则结束。由此则可得到对应各离散期望位移所对应的输入电压，即得到平台的离散Preisach逆模型。

第2种情况是位移信号存在间断点，如方波信号，根据上述算法可知，在间断点处r(k)与r(k-1)之间的差值较大，会增加迭代次数，增长搜索时间，不便于实时控制，可以采用二分法迭代加快搜索速度，算法流程如图3(b)所示。该算法与定步长迭代搜索法不同之处在于α(k)的迭代更新，主要在于搜索区间边界的确定。根据目标位移r(k)与r(k-1)的差值d(k)选择电压搜索区间，设定αmax与αmin分别为平台输入电压的最大值和最小值。若d(k)>0，α(k)搜索范围设定为[α(k-1),αmax]；若d(k)<0，α(k)搜索范围设定为[αmin,α(k-1)]，其中α(k)为该区间的中心点。根据g(k)与r(k)之间的偏差调整区间进行二分迭代搜索，若偏差大于精度要求E(k)且E(k)>0，则修改搜索区间的左边界为α(k)；若偏差大于精度要求E(k)且E(k)<0，则修改搜索区间的右边界为α(k)，直至其差值小于E(k)。

2.2 复合控制器

基于离散Preisach逆模型的前馈控制，利用其逆模型进行迟滞补偿，可消除压电陶瓷驱动器迟滞现象对微操作平台的影响，加快平台的响应速度，减小稳态误差，但由于该逆模型存在偏差，其稳态控制精度不够理想。PID控制具有较好的响应快速性和稳定精度，并且其算法简单，实时性好，易于实现。为达到微操作平台的高精度和快响应性要求，将PID和前馈控制相结合构成复合控制。当误差较小时，增强前馈控制作用以加快系统响应速度；当误差较大时，增强PID控制的作用来实现无稳态误差的调节目标。

如图4所示，该控制系统由前馈控制环和PID控制环两部分组成。在前馈环中，基于迟滞逆模型，获得前馈补偿电压uh(k)；在反馈环中，期望位移和实际输出位移比较，所得误差e(k)作为PID控制器输入，获得附加补偿电压ue(k)。基于前馈补偿PID控制算法可表示为

u(k)=uh(k)+ue(k)=H-1(r(k))+

(12)

其中：H-1(r(k))为离散Preisach逆模型；Kp，Ki，Kd分别表示PID比例、积分和微分系数。

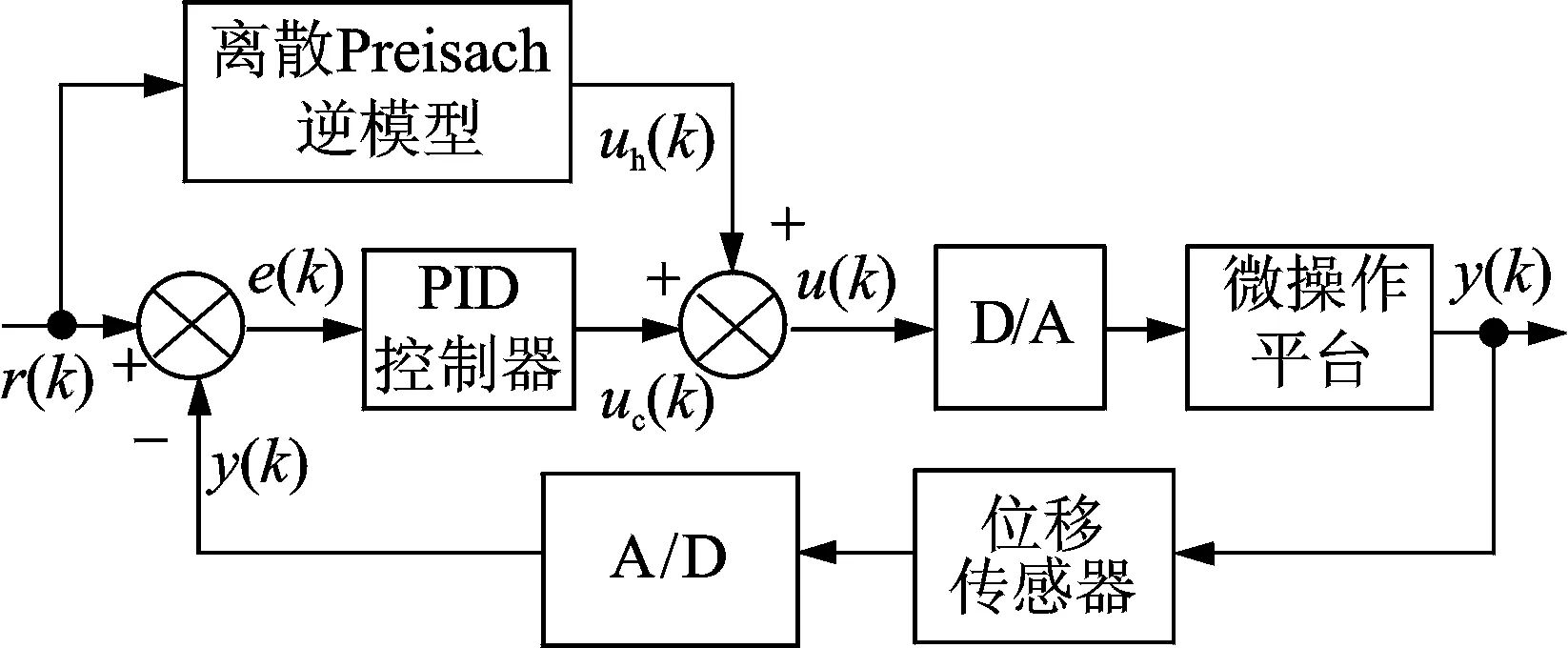
图4 复合控制算法Fig.4 Compound control algorithm

为了整定PID参数，需要建立微操作平台的动力学模型，平台主要由柔顺机构和压电陶瓷驱动器组成。驱动器输出位移到输入电压之间的传递函数可等效为1阶惯性系统

(13)

其中：K1为放大系数；T0为时间常数。

柔顺机构可简化为质量-弹簧-阻尼系统，柔顺机构的输出位移与压电陶瓷驱动器输出位移之间的传递函数可表示为

(14)

其中：ωn为柔顺机构的无阻尼固有频率；K2为放大系数；ξ为阻尼比。

联合式(13)和式(14)可得微操作平台的传递函数为

(15)

由式(15)可知，要确定平台的模型，需要确定参数K1，T0，K2，ωn和ξ，可采用实验方法得到。根据式(15)所示的模型采用ZN临界比例法[15]整定PID参数。

3 实验验证

3.1 获得Preisach逆模型

实验配置如图5所示，由柔顺机构、压电陶瓷驱动器、位移传感器、信号调理器、D/A卡及工控机组成。压电驱动器为哈尔滨芯明天公司生产的80VS12，位移传感器为PI 公司生产的D-E20.200，分辨率为0.2μm，线性度为0.3 %，D/A卡和A/D卡分别为NI公司的PCI-6713和PCIe-6341。

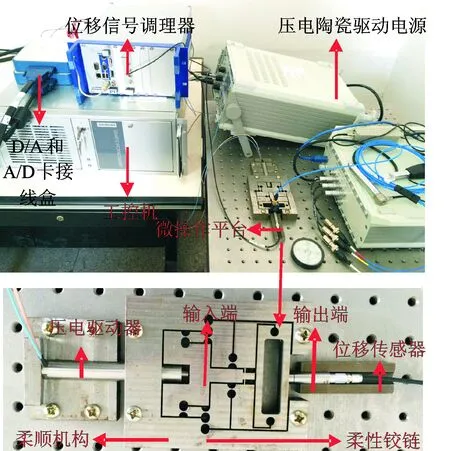
图5 实验配置Fig.5 Experiment setup

首先，基于支持向量机建立微操作平台的离散Preisach模型。压电驱动器的饱和电压Um为120 V，设电压等分数n为16，当驱动器输入电压从0上升至各等分点电压120j/16(j=1,2，…,16)及下降至0，可得如图6所示的回环电压序列(120j/16,120j/16)和(120j/16,120m/16)(m=j-1,j-2,…，1)，各电压序列所对应的输出位移如图7所示。将图7所示的x(αi,βj)代入式(2)可得到f(αi,βj)，则可得到如表1所示的用于建立支持向量机回归模型的训练样本点。采用栅格搜索方法可求得参数c=1.5，h=36.7，采用支持向量机训练可得f(α,β)与(α,β)之间关系的回归模型F(z)如图8所示。为了说明回归模型的精确性，样本点的实测位移与由回归模型得到的预测位移之间的误差如图9所示，误差值范围为[-0.15,0.15]μm，说明所建立模型的正确性。

图6 回环电压序列Fig.6 Loop voltage sequence

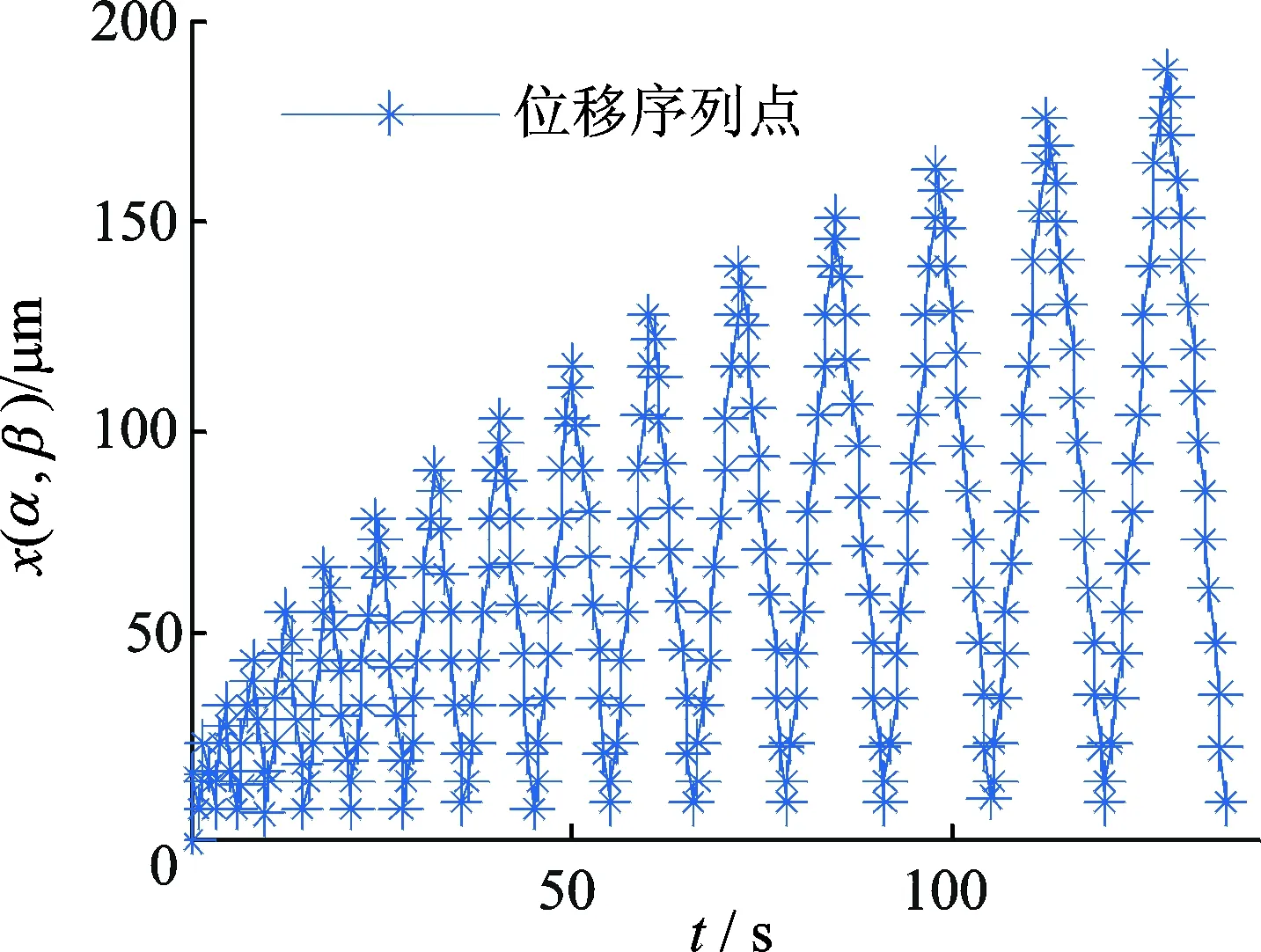
图7 回环电压序列所对应的输出位移Fig.7 Output displacements corresponding to loop voltage sequence

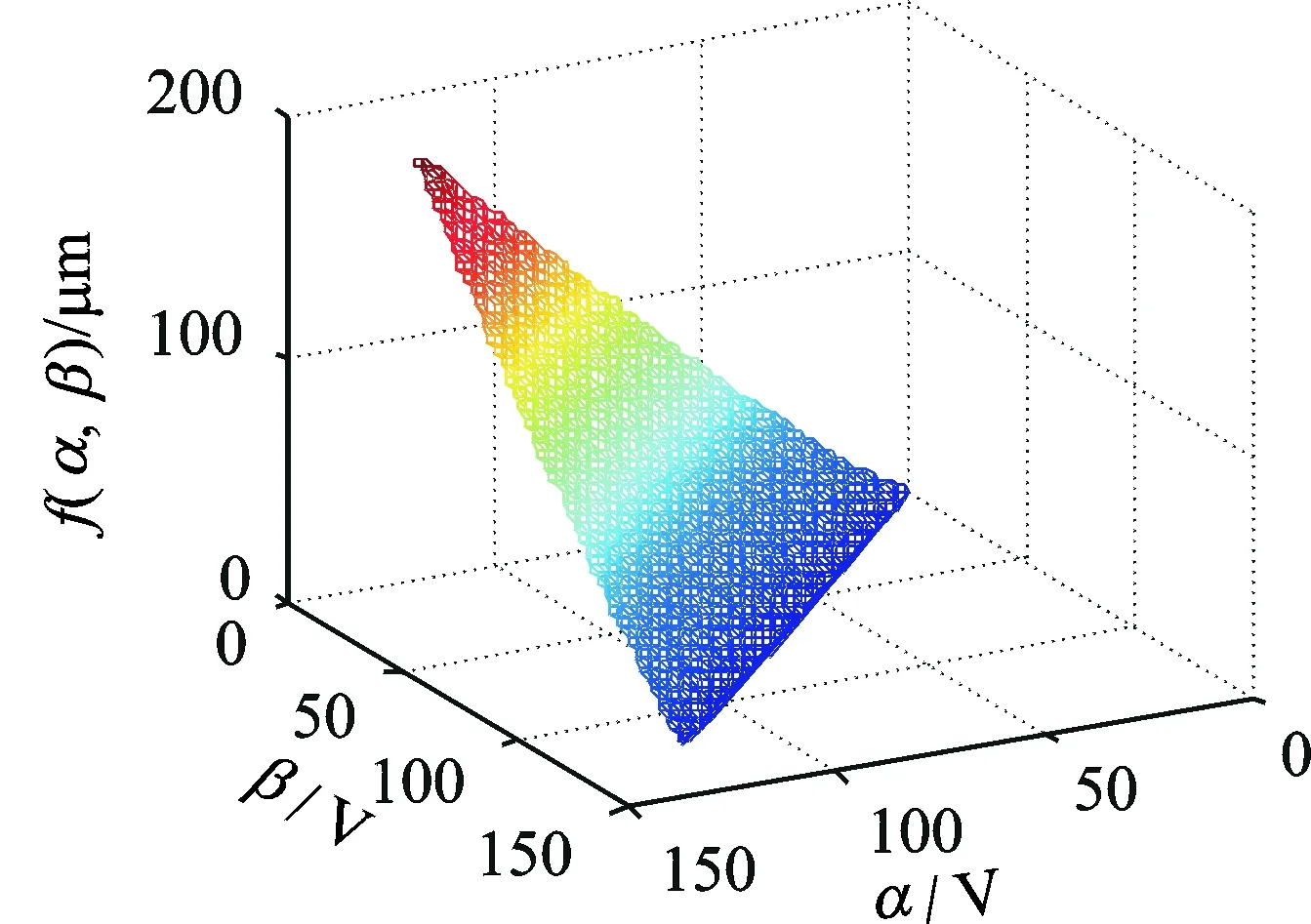
图8 支持向量机回归模型Fig.8 The model of support vector regression

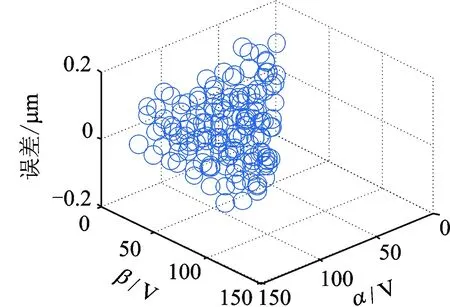
图9 预测误差Fig.9 Prediction error

然后，采用实验方法确定式(15)传递函数的参数。对平台施加某阶跃电压信号，分别得到所对应的驱动器输出位移和平台输出位移的阶跃响应。通过阶跃响应实验测量得到驱动器的稳态值与稳定时间，根据控制理论可以得到参数K1与T0分别为0.01和10.325。式(14)表明柔顺机构为2阶系统，通过测量平台的阶跃响应稳态值可得K2=1.622，ωn与ξ可以采用实验模态测试得到，分别为231 Hz和0.159。根据所得的参数T0，K1，K2，ωn与ξ，由式(15)可求得微操作平台的传递函数为

(16)

根据式(16)，采用ZN临界比例法可得PID参数分别为Kp=0.01，Ki=0.04，Kd=0.001。

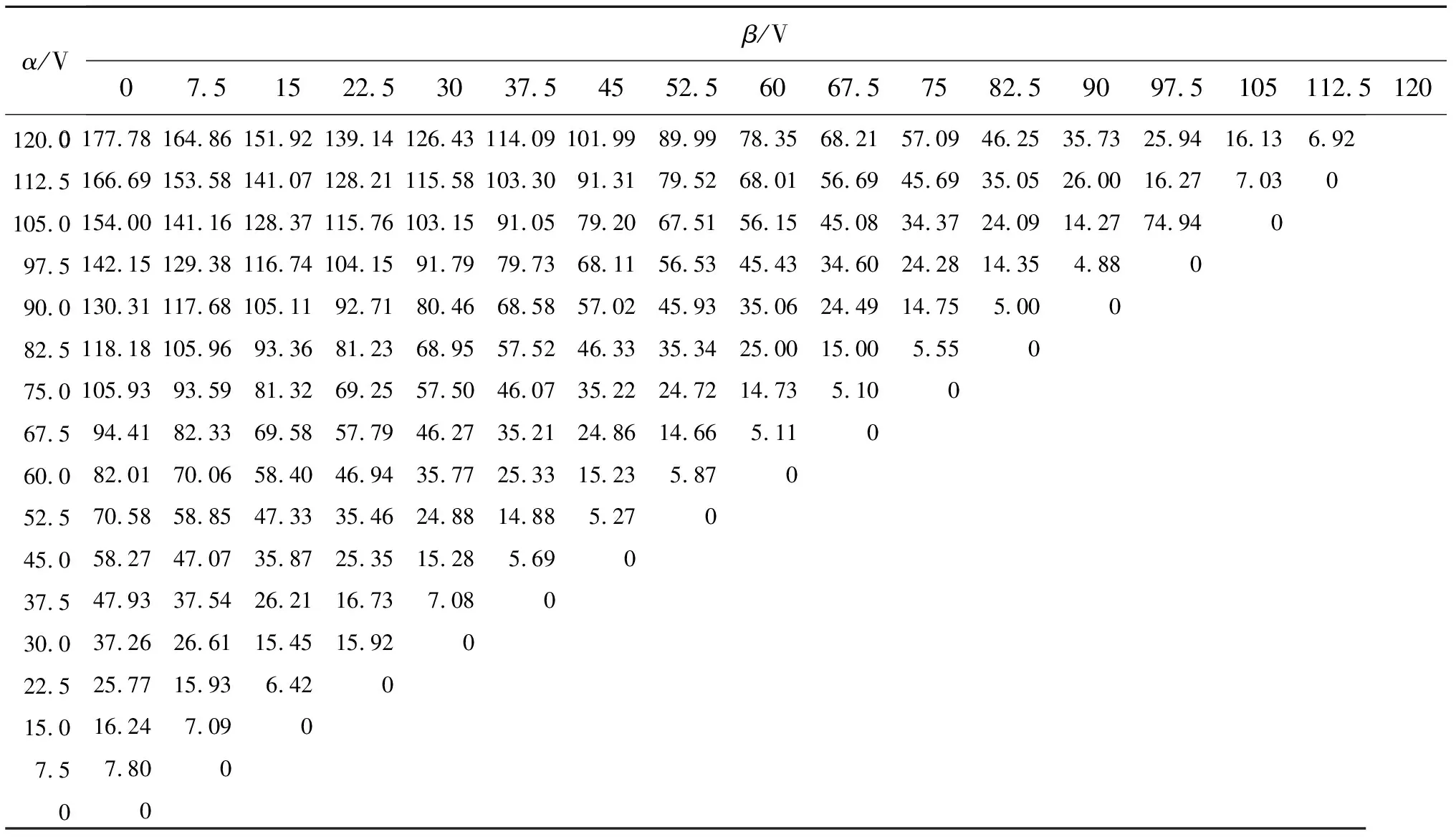
表1 样本点

3.2 实验验证

首先分析基于离散Preisach逆模型的前馈控制的可行性，设微操作平台期望位移为某阶跃信号r(t)=20(t≥0)，采样时间T和采样周期Ts分别为2 s和0.001 s，αmax=120 V，αmin=0 V，步长Δα=0.01 V，E=0.1 μm。分别采用基于二分法与定步长迭代搜索方法求解Preisach逆模型进行前馈控制，图10为在前馈控制作用下的平台阶跃响应。由图10可知，当采用前馈控制时，平台输出位移无振荡，基于二分法的前馈控制稳态误差为2.5 μm，调整时间为0.05 s，基于定步长的前馈控制稳态误差约为3.4 μm，调整时间为0.15 s，所以，相比于定步长法，二分法迭代具有更快的响应速度和更高的跟踪精度。

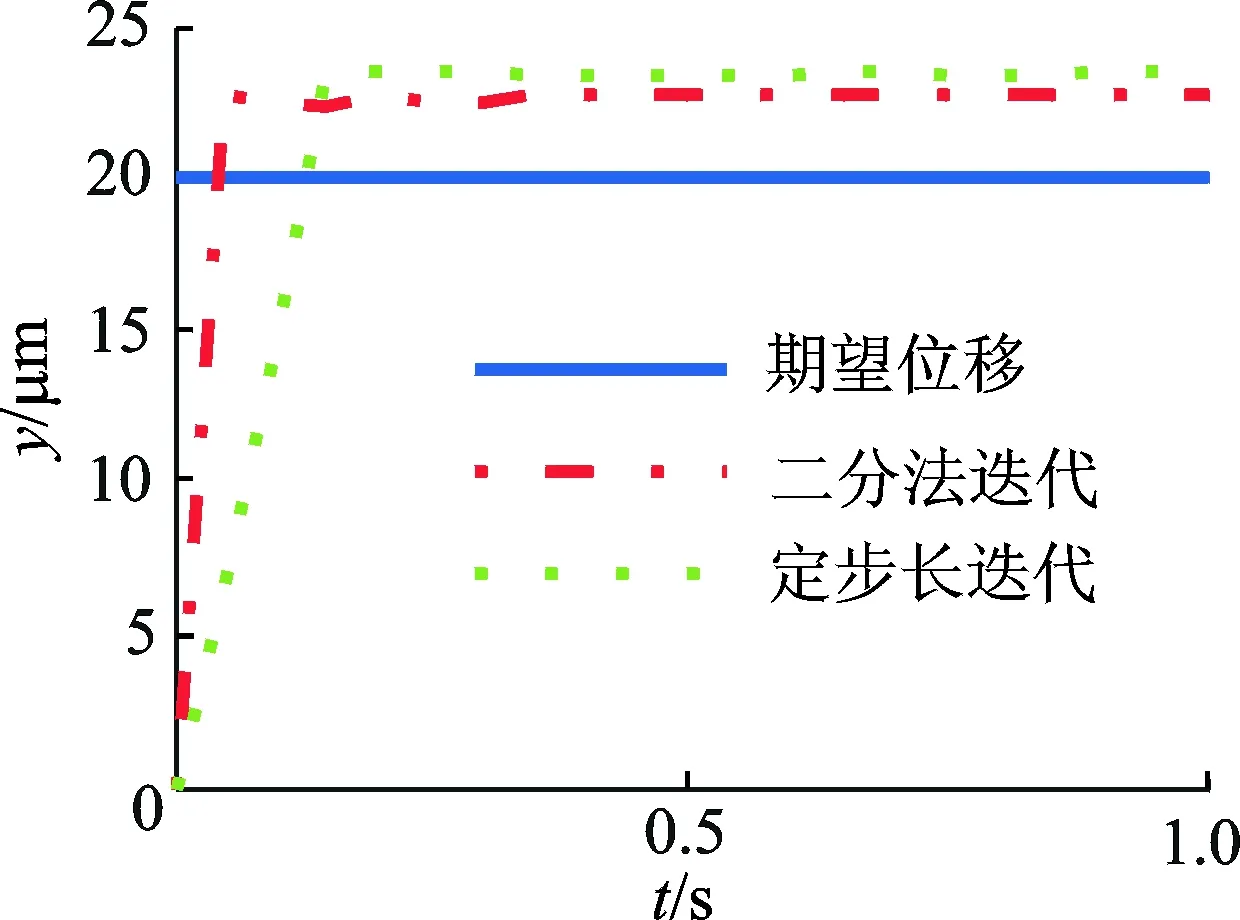
图10 前馈控制作用下的阶跃响应Fig.10 Step response under the feedforward control

为了验证所提出的复合控制算法的有效性和优越性，分别采用前馈控制、PID控制与复合控制进行运动跟踪实验研究。图11表示平台分别在复合控制、前馈控制和PID控制作用下的阶跃响应，不同控制算法的平台性能指标如表2所示。由图11和表2可得出如下结论：a.从响应速度看，复合控制与前馈控制调节时间相近，较PID更快；b.从振荡情况看，前馈控制超调量最大，但振荡较小，复合控制与PID超调量基本相同，复合控制衰减更快；c.从稳态精度看，复合控制的稳态误差最小，前馈控制最大。由上述比较分析可知，所提出的复合控制算法具有较好的综合动态性能，能消除压电迟滞现象的影响。图12表示复合控制各电压uh，ue与u的变化情况，由图12可知，复合控制输出电压u是在前馈输出电压uh基础上通过PID输出电压进行调节获得，复合控制结合了前馈和PID两种控制算法的优势，前馈控制可提高平台的响应速度，PID能够消除前馈控制的稳态误差。

图11 3种控制器作用下的阶跃响应Fig.11 Step responses under three controllers

图12 复合控制各输出电压变化情况Fig.12 The change of output voltage under compound control

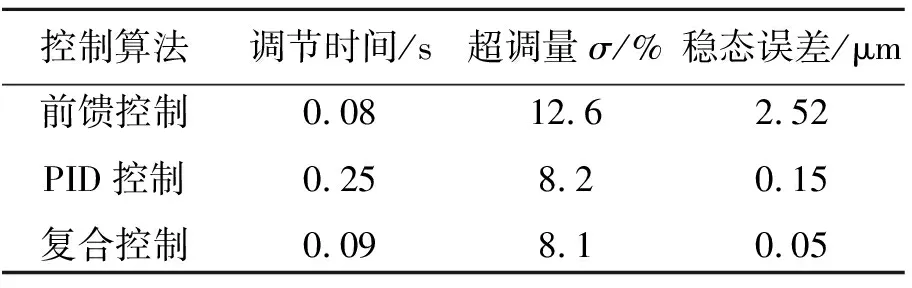
表2 性能比较

为了验证复合控制算法能对微操作平台的任意位移信号进行跟踪，设期望位移范围为[0,80]μm，在复合控制作用下平台的实际位移如图13所示。图14表示跟踪误差，误差范围为[-2,+2]μm，误差率为2.5 %，由图13和图14可知，平台在复合控制作用下能较好地跟踪任意输入位移。

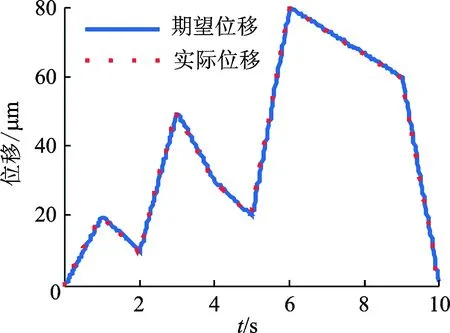
图13 对任意信号的跟踪Fig.13 Tracking any signal

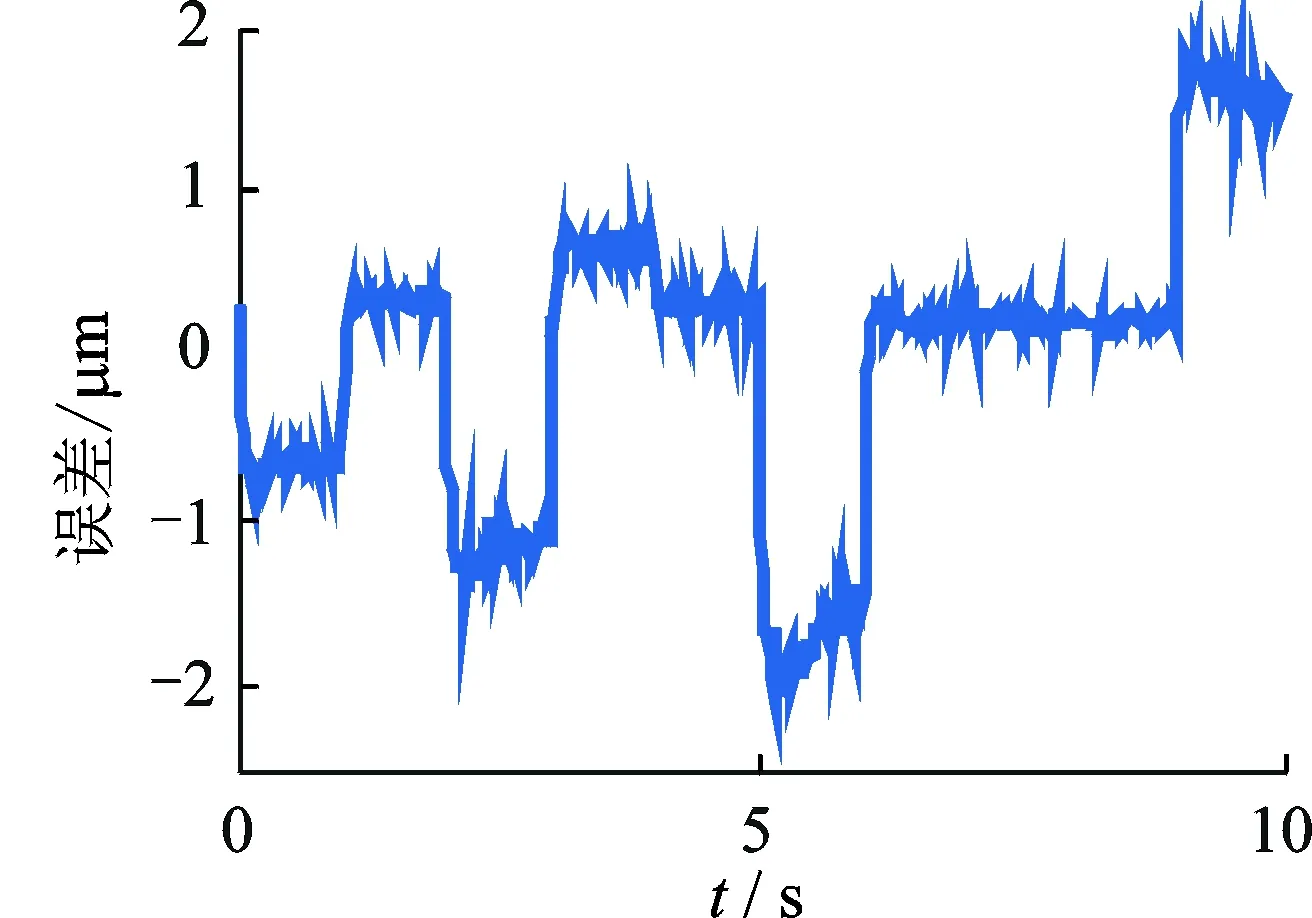
图14 对任意信号的跟踪误差Fig.14 Tracking error of any signal

4 结束语

为了解决压电陶瓷驱动型微操作平台的迟滞非线性问题，提高微操作平台的运动跟踪精度，提出了一种基于离散Preisach逆模型的前馈补偿与PID反馈调节相结合的复合控制算法。提出一种联合支持向量机与Preisach模型建立反映微操作平台迟滞现象的回归模型，并基于该模型采用迭代搜索方法获得其逆模型进行前馈控制。为了说明所提出的控制算法的优越性，分别与PID和前馈控制算法进行实验比较分析。实验结果表明，所提出的复合控制算法跟踪误差更小，跟踪速度更快，说明该控制方法的控制精度高、动态特性好。

参 考 文 献

[1] 胡俊峰, 徐贵阳, 郝亚洲. 基于响应面法的微操作平台多目标优化 [J]. 光学精密工程, 2015, 23(4): 1096-1104.

Hu Junfeng, Xu Guiyang, Hao Yanzhou. Multi-objective optimization of a novel micro-manipulation stage based on response surface method [J]. Optics and Precision Engineering, 2015, 23(4): 1096-1104. (in Chinese)

[2] 胡俊峰, 郝亚洲, 徐贵阳 等. 一种新型微操作平台的精确运动控制 [J]. 机械科学与技术, 2016, 35(2): 216-221.

Hu Junfeng, Hao Yanzhou, Xu Guiyang, et al. Precision motion control of a novel micro-manipulation stage [J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(2): 216-221. (in Chinese)

[3] 张宪民, 龙学俊, 林容周. 基于视觉的三自由度微动平台输入耦合研究[J]. 振动、测试与诊断, 2013, 33(1):1-5.

Zhang Xianmin，Long Xuejun，Lin Rongzhou. Research on input couple of 3DOF micro positioning stage based on vision [J].Journal of Vibration， Measurement & Diagnosis，2013, 33(1):1-5. (in Chinese)

[4] 胡俊峰, 郝亚洲, 徐贵阳. 传递矩阵法分析平面柔顺机构的振动特性[J]. 振动、测试与诊断, 2015, 35(6):1145-1151.

Hu Junfeng, Hao Yanzhou, Xu Guiyang. Mechanical vibration modeling and analysis of planar compliant mechanisms based on transfer matrix method [J]. Journal of Vibration， Measurement & Diagnosis, 2015, 35(6):1145-1151. (in Chinese)

[5] Vominh T, Tjahjowidodo T, Ramon H, et al. A new approach to modeling hysteresis in a pneumatic artificial muscle using the Maxwell-slip model [J]. IEEE/ASME Transaction on Mechatronics, 2011, 16(1): 177-186.

[6] Lin C J, Lin P T. Tracking control of a biaxial piezo-actuated positioning stage using generalized Duhem model [J]. Computers & Mathematics with Applications, 2012, 64(5): 766-787.

[7] Xiao Shunli., Li Yangmin. Modeling and high dynamic compensating the rate-dependent hysteresis of piezoelectric actuators via a novel modified inverse Preisach model [J]. IEEE Transactions on Control Systems Technology, 2013, 21(5): 1549-1557.

[8] Jiang Hao, Ji Hongli, Qiu Jinhao, et al. A modified prandtl-ishlinskii model for modeling asymmetric hysteresis of piezoelectric actuators [J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 2010, 57(5): 1200-1210.

[9] 刘国华, 李亮玉. 基于混合闭环控制器的三维超微定位平台的研究 [J]. 压电与声光, 2010, 32(5): 800-802.

Liu Guohua, Li Liangyu. Study on the performances of 3D ultra-micropositioning system based on hybrid controller [J]. Piezoelectrics & Acoustooptics, 2010, 32(5): 800-802. (in Chinese)

[10] Liaw H C, Shirinzadeh B. Robust adaptive constrained motion tracking control of piezo-actuated flexure-based mechanisms for micro/nano manipulation [J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1406-1415.

[11] 李黎, 刘向东, 王伟, 等. 压电陶瓷执行器迟滞特性的广义非线性Preisach模型及其数值实现 [J]. 光学精密工程, 2007, 15(5): 706-712.

Li Li, Liu Xiangdong, Wang Wei, et al. Generalized nonlinear Preisach model for hysteresis nonlinearity of piezoceramic actuator and its numerical implementation [J]. Optics and Precision Engineering, 2007, 15(5): 706-712. (in Chinese)

[12] Chang C C, Lin C J. LIBSVM: a library for support vector machines [J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3): 389-396.

[13] Smola A J, Schölkopf B. A tutorial on support vector regression [J]. Statistics and Computing, 2004, 14(3): 199-222.

[14] 纪昌明, 周婷, 向腾飞, 等. 基于网格搜索和交叉验证的支持向量机在梯级水电系统隐随机调度中的应用 [J]. 电力自动化设备, 2014, 34(3): 125-131.

Ji Changmin, Zhou Ting., Xiang Tengfei, et al. Application of support vector machine based on grid search and cross validation in implicit stochastic dispatch of cascaded hydropower stations[J]. Electric Power Automation Equipment, 2014, 34(3): 125-131. (in Chinese)

[15] 刘玲玲. PID参数整定技术的研究及应用 [D]. 郑州: 郑州大学, 2010.