薄壁硬壳式圆筒结构的屈曲分析

王骁峰，段 毅，袁锐之

(空间物理重点试验室， 北京 100076)

硬壳结构是最简单的薄壁结构[1]，圆柱筒壳由于特殊的几何构型和优良的受力性能，被广泛应用于船舶工程、导弹火箭外壳及航空航天等许多工程技术领域[2]，如火箭、导弹的仪器舱、贮箱、发动机燃烧室等。圆筒硬壳结构在火箭等飞行器的飞行过程中，飞行器舱段的薄壁圆筒壳受到轴向压力往往会在强度破坏之前失稳(发生屈曲)，使飞行器的结构承载失效。均匀轴压下圆柱薄壳的极限承载能力对初始几何缺陷非常敏感。Tennyson[3]等人研究了局部轴对称缺陷对圆柱薄壳屈曲性能的影响，指出局部缺陷会大大降低结构的承载性能。叶军等的研究也表明[4]，环向初始缺陷是影响薄壁钢桶临界屈曲载荷的主要因素。

对于圆筒硬壳结构来说，由于加工工艺、加工误差等原因，使得圆筒壳不可避免的存在几何缺陷，即存在纵向和环向结构上的不对称性，如焊缝、同轴度误差、不圆度误差以及局部凹凸不平等等，这种不对称性导致临界轴压明显降低。造成缺陷的原因还有存储、运输、安装和使用等[5]。但加工误差所造成的初始几何缺陷是壳体承载能力下降的主要原因[6]。在进行壳体屈曲特性研究时，最为理想的情况是引入真实几何缺陷，但是，由于壳体加工工艺不同，批次不同，产生的几何缺陷也不同，即使同一批次产品的几何缺陷也具有随机性，这就需要通过大批量、相似壳体试验，建立真实几何缺陷的可靠性模型，往往费时费力，收效甚微[6]。因此，引入等效几何缺陷的方法研究壳体屈曲特性就十分必要。Tennyson[3]研究局部轴对称缺陷对钢筒屈曲性能的影响时，发现即使只有一条轴对称缺陷，也会使薄壁筒壳的屈曲临界载荷有较大的降低，Koiter[7]首次研究了非完善壳体稳定性的一般准则，提出了“缺陷敏感度”的概念，揭示了屈曲的跳跃性与原始初始缺陷理论的相互关系。文献[8]表明圆筒环向焊缝缺陷会导致最低的屈曲承载力，而缺陷最不利位置可通过无缺陷圆筒非线性屈曲模态确定[8]。欧洲法规EN1993-1-6(2007)[9]规定，几何缺陷的形状应取最差缺陷(即导致壳体屈曲载荷下降最快的缺陷)，在最差缺陷形状未知的情况下，建议采用模态缺陷分析壳体的屈曲特性。

初始缺陷的形式一般分为特征值屈曲模态缺陷、环向焊缝缺陷、随机缺陷、实测缺陷等[10]。对于结构的实际缺陷来说，在产品失效之前，无法预知缺陷的性质、位置和和缺陷程度，无法对后三种缺陷的屈曲问题进行前瞻性分析。工程上常常采用特征值屈曲模态缺陷进行分析，无需知道缺陷的性质、位置和和缺陷程度。对于壳体来说，只需给出壳体的线性特征值屈曲模态和一定百分比的壳体厚度作为初始几何缺陷。对于网格加筋的圆筒结构、锥形圆筒结构等，求解壳体稳定性问题时，均可以当量成光壁圆筒结构[11]。本文研究表明，通过基于屈曲模态缺陷的非线性屈曲分析来求解圆筒结构的临界失稳轴压，用于工程设计是可行的。

1 非线性屈曲的描述

对于板、壳、杆、梁等结构，当其所受的外载荷达到一定值的时候，结构失稳，此时无需增大外载荷，甚至在外载荷减小的情况下，结构的变形继续增大，即结构的刚度为零，甚至为负。随着变形的增大，结构又开始恢复抵抗变形的能力，即结构发生了屈曲。第一次失稳发生前的过程称为前屈曲，第一次失稳的后继过程称为后屈曲。

当结构处于理想状态、无任何物理缺陷和几何缺陷时，结构的弹性失稳表现为歧点(分岔点)失稳；对结构的屈曲分析可以用线性特征值描述，通过求解特征值可以确定结构的临界失稳载荷。这个分析过程也是一个典型的前屈曲分析过程，如图1中理想加载路径所示。但实际结构不可能是理想结构，几何不对称因素(几何缺陷)是不可避免的。结构的稳定性对初始几何缺陷十分敏感，结构的失稳过程如图1中所示非理想结构加载路径。结构失稳的形式是驻点失稳，失稳的过程是一个几何非线性过程，此时对屈曲过程的描述应采用非线性描述，由图1可以看出，特征值屈曲的歧点所对应的临界压力值是非保守解，而结构的实际临界压力值应该是驻点所对应的临界压力值。

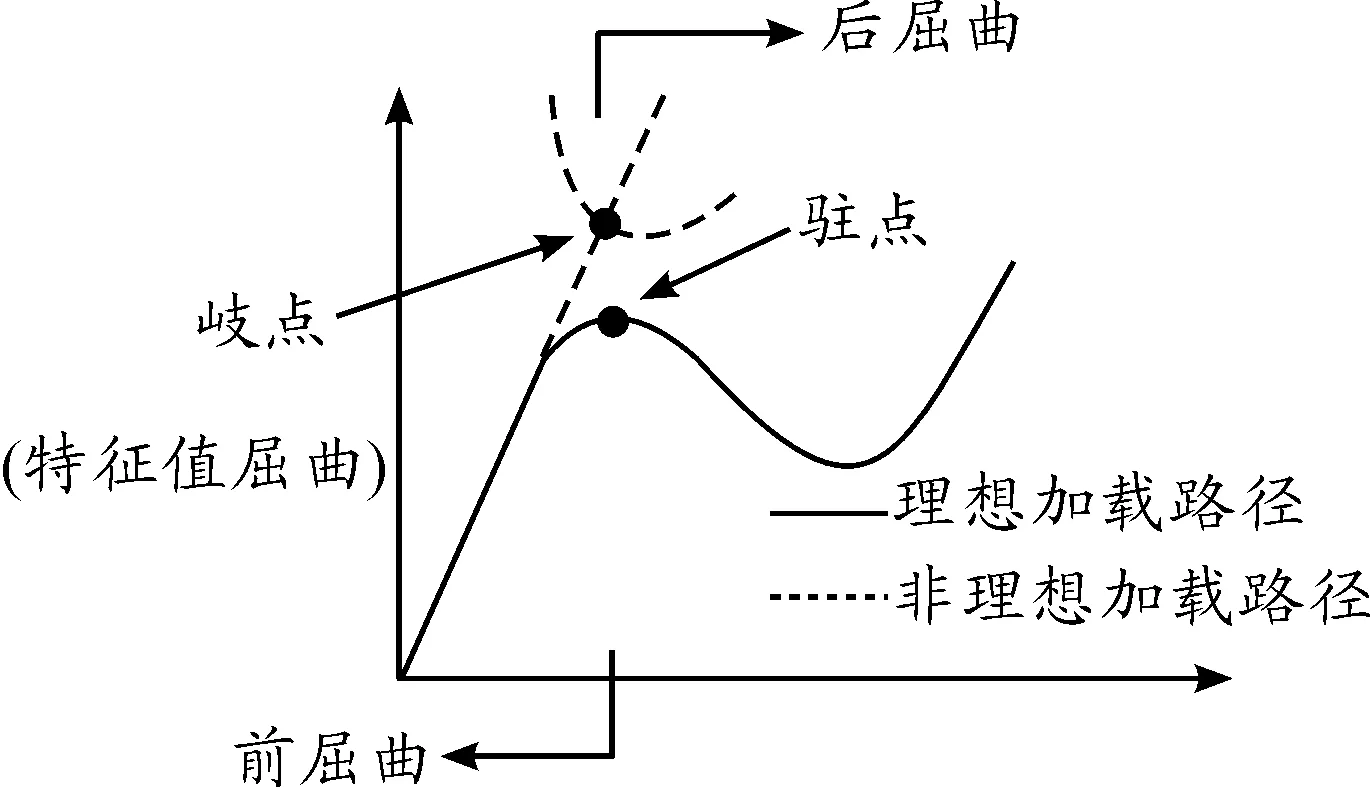
图1 结构屈曲的载荷(F)-位移(u)示意图

2 特征值屈曲

结构在外载荷作用下任意状态时的增量平衡方程是

(1)

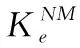
(2)

达到失稳状态时，结构失去进一步抵抗变形的能力，此时应有ΔPN≈0，而增量平衡方程变为

(3)

因此，线性屈曲转化为特征值问题。最小特征值λ代表了临界载荷比例因子，特征向量ΔuM代表了失稳模态。

3 广义弧长法求解非线性屈曲

非线性屈曲的求解一般采用广义弧长法，即每一个增量步是弧长步而不是载荷步。在图2所示的求解空间里，弧长法是借助一个弧面将载荷因子增量Δλ和位移增量ΔuN关联起来。

其中，弧长由下式决定

(4)

图2表示一个弧长步内的迭代求解过程；一个非线性问题的求解过程是由多个弧长步组成。

4 修正的Riks算法

4.1 初始载荷因子增量的求解

修正的Riks算法即修正的弧长法，其特点是用“平面”代替“弧面”，具有求解精度好、效率高等特点，为ABAQUS所采用。在多维求解空间里，修正的Riks法(Modified Riks algorithm)的求解过程如图3所示。

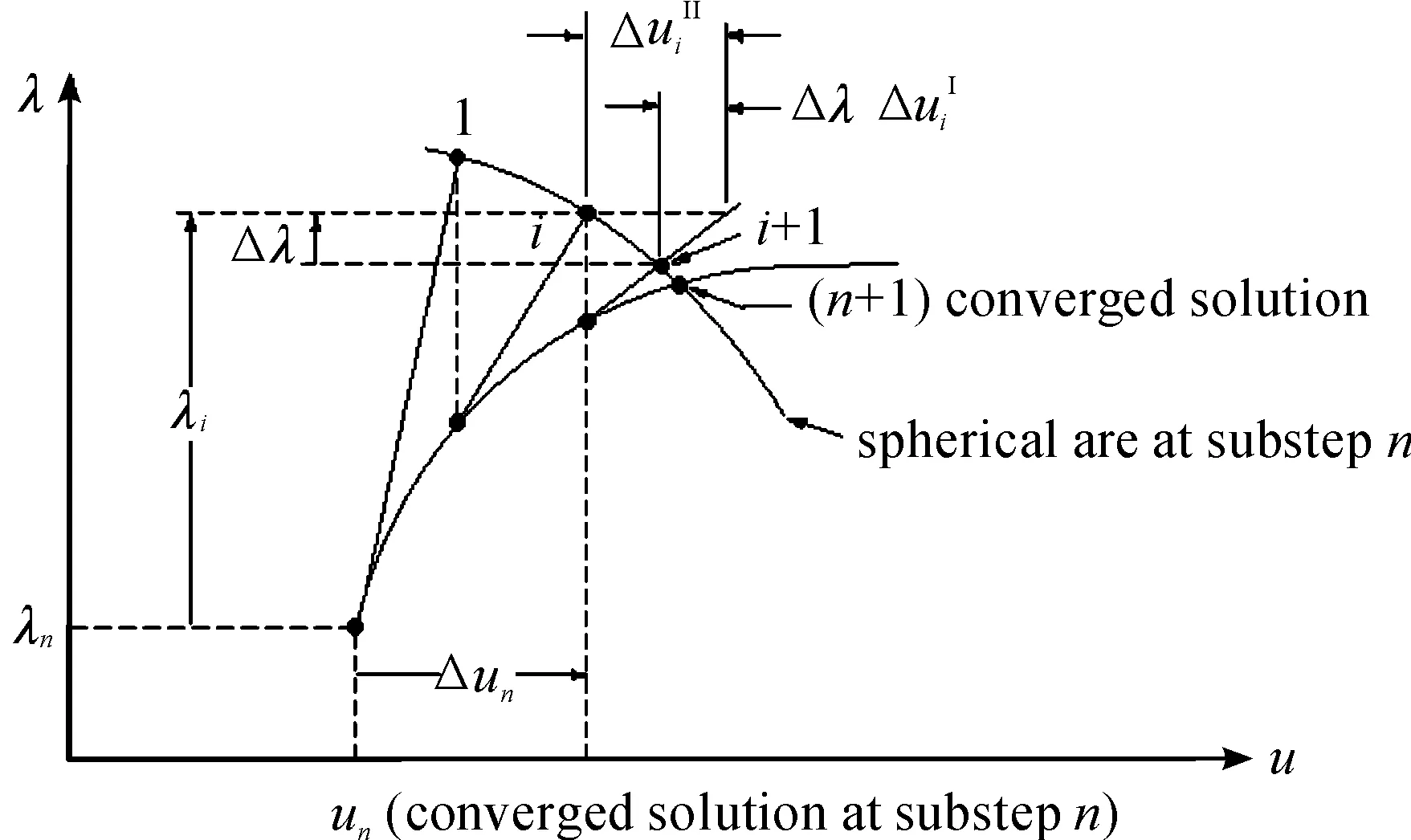
图2 弧长法求解非线性屈曲

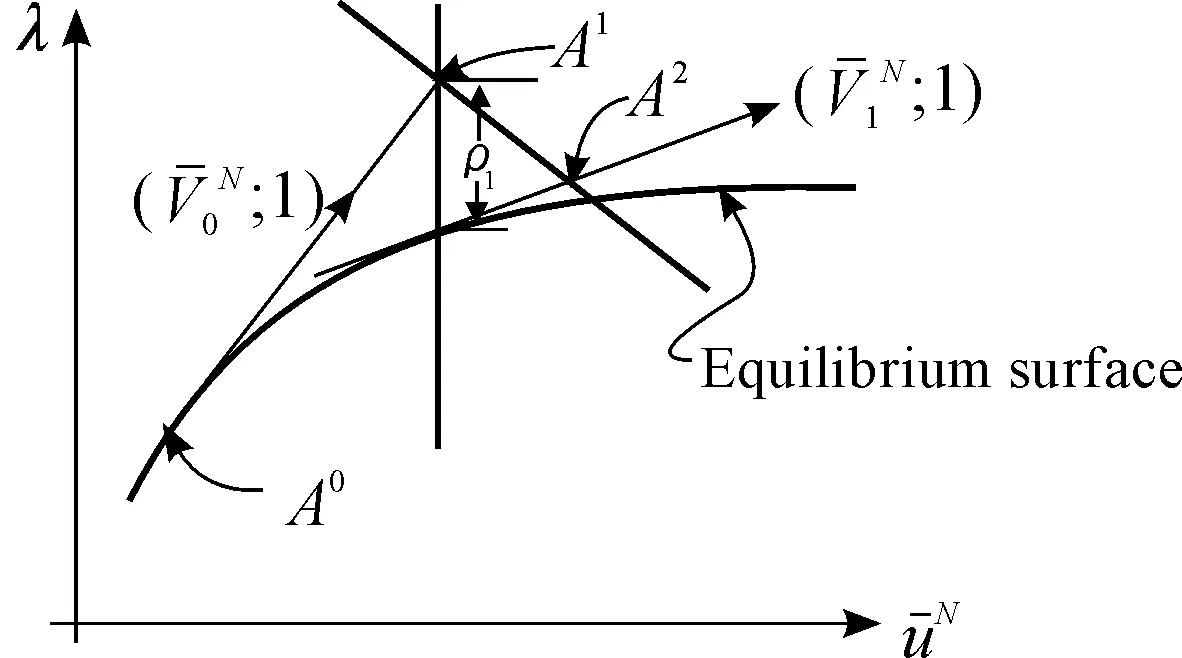
图3 修正的Riks算法求解非线性屈曲

(5)

第一个弧长Δl的大小由用户指定。则应有

(6)

(7)

从而

(8)

此处

(9)

求得Δλ0以后，开始进行如下过程的迭代。

载荷因子增量及位移增量初始化，有

Δλi=Δλ0

(10)

(11)

4.2 迭代过程

在第i个迭代步，形成节点应力矩阵IN，切线刚度矩阵KNM

(12)

(13)

其中βN是应变位移转换矩阵。这样，求解空间中的力和位移的预测点Ai所对应的状态为

(14)

检查迭代平衡

(15)

式(15)为解空间点Ai所对应的力和节点力产生的残差力。若残差力足够小，达到收敛标准，则该弧长步的迭代收敛，下一个弧长步的迭代开始。若达不到收敛标准，则继续迭代求解。

(16)

(17)

可求得：

(18)

这样就确定了Ai+1的位置，其对应的状态为

(19)

更新变量，返回到式(10)，准备下一个迭代：

(20)

Δλi+1=Δλi+μ

(21)

i=i+1

(22)

(23)

5 算例

长度L=600 mm，半径R=300 mm，厚度t=2 mm，弹性模量E=70 000 MPa，泊松比μ=0.3的圆筒壳，底部简支，自由端施加轴向压力，分析轴压稳定性。

5.1 根据工程计算公式求解

航天飞行器结构设计应用中，对大量圆柱壳体的轴压稳定性试验的数据进行统计，归纳出如图4的设计曲线，即轴压临界应力系数k0～R/t曲线。根据图4所示的曲线查取相应的k0，再根据公式σcr=k0Et/R进行计算。

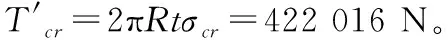
由图4可以看出，根据设计曲线求得的临界轴压非常保守。

图4 轴压临界应力系数k0～R/t曲线

5.2 有限元法

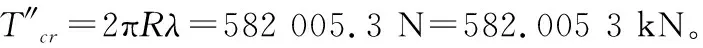
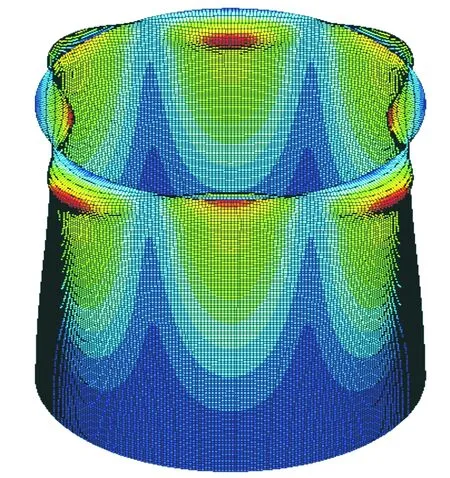
图5 特征值屈曲模态

由计算分析看出，非线性屈曲的临界应力T‴明显低于特征值屈曲求得的临界应力T″，略高于经验公式求得的临界应力T′。非线性屈曲的临界应力T‴和经验公式的临界应力T′之比为T‴/T′=1.1/1，二者比较接近。

改变圆筒壳的长度和厚度，同样可以进行非线性屈曲的求解。几种工况下有限元非线性屈曲分析求得的临界轴压和工程公式计算得到的临界轴压之比T‴/T′如表1所示。由表1可见，有限元非线性屈曲的临界轴压计算结果和采用工程公式的计算结果吻合度较好。其中，t=3 mm时k0可取0.26。

图6 非线性屈曲失稳变形

图7 载荷比例因子和弧长的关系

L=600 mmL=900 mmL=1 200 mmt=2 mm1.1/11.1/11.05/1t=3 mm1.01/11.04/11.02/1

对应上述6种工况的线性特征值屈曲模态和非线性屈曲失稳变形图如图8～图13所示。每个图的左图为线性屈曲模态示意图，云图为位移，右图为非线性屈曲失稳示意图，云图为MISES应力。

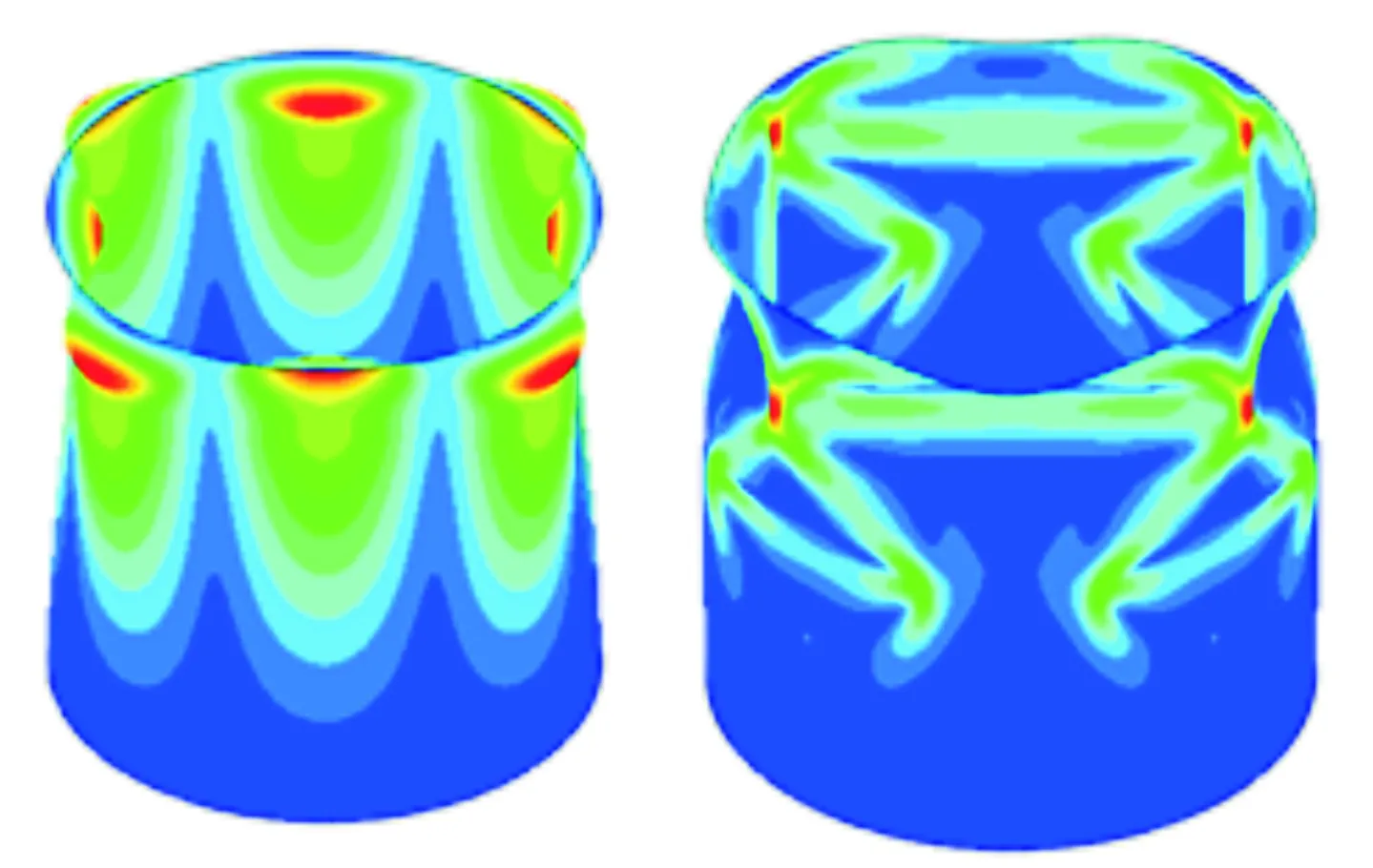
图8 L=600 mm，t=2 mm时屈曲变形

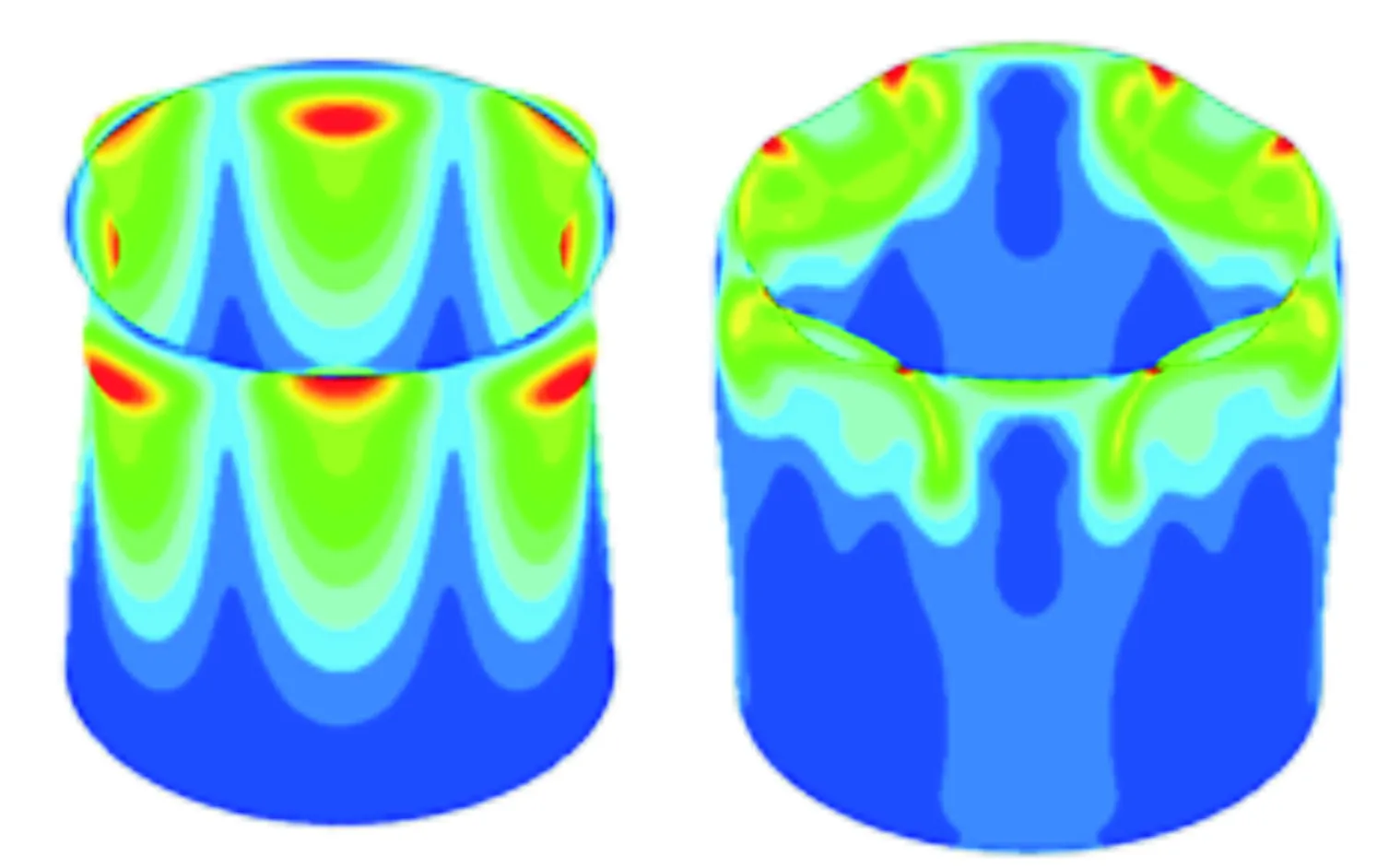
图9 L=600 mm，t=3 mm时屈曲变形

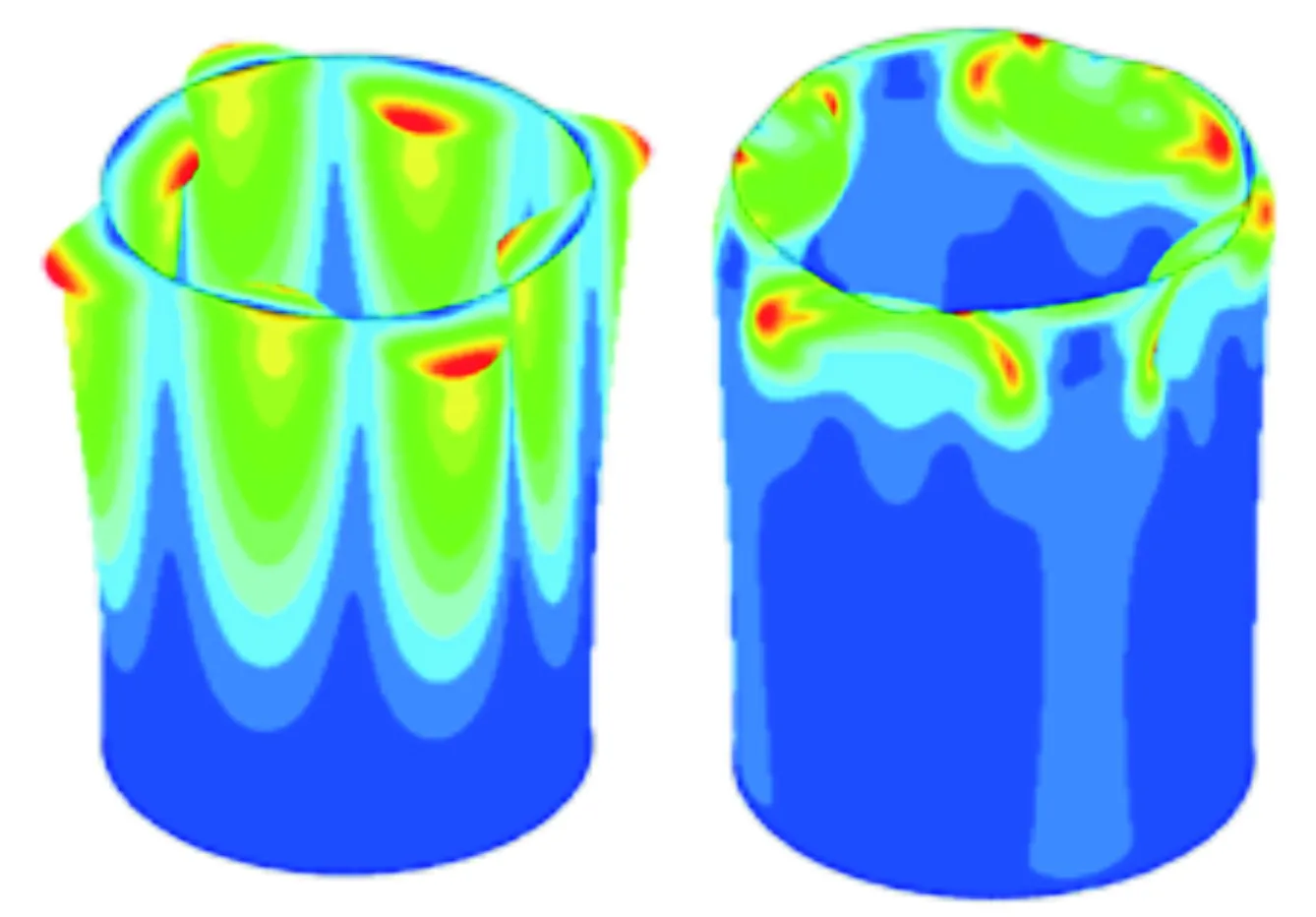
图10 L=900 mm，t=2 mm时屈曲变形

图11 L=900 mm，t=3 mm时屈曲变形

图12 L=1 200 mm，t=2 mm时屈曲变形

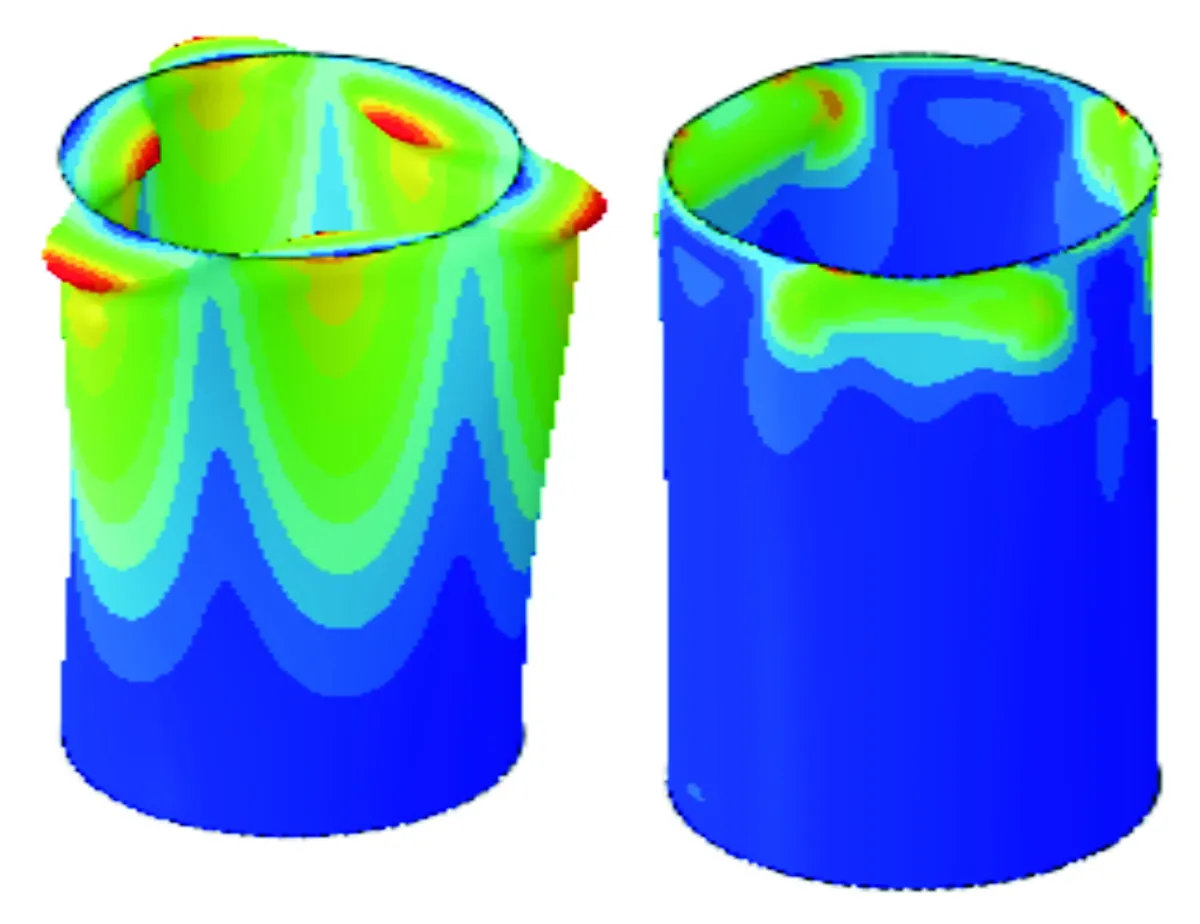
图13 L=1 200 mm，t=3 mm时屈曲变形

6 结论

1) 采用特征值屈曲模态缺陷和修正的Riks算法，对薄壁圆筒进行了屈曲分析，并将分析结果和工程计算公式的分析结果进行了对比，二者具有一致性。

2) 有限元法对任意结构均能求解。对于无法用公式求得临界轴压的结构，采用基于特征值屈曲模态缺陷的弧长法进行非线性屈曲求解，可以得到合理的结果。

3) 采用特征值屈曲模态缺陷进行分析，不必事先知道缺陷的具体位置和缺陷的性质，在特征值屈曲的基础上引入厚度的10%作为缺陷参数，采用弧长法进行非线性屈曲分析，可以满足工程设计需要，尤其是在工程研制的方案阶段，在没有真实产品用来进行试验的情况下，采用这种方法进行前瞻性的设计和分析，具有重要的意义。