基于EMD与RVM-GM模型的故障率预测
2018-07-31王瑞奇
王瑞奇,逯 程
(海军航空大学, 山东 烟台 264001)
随着装备集成化水平的提高,其组成结构日趋复杂,退化故障问题使装备保障工作面临严峻挑战。实现装备故障率的准确预测可以为视情维修策略的制定提供建设性的指导,同时为装备部门进行下一步的备件采购任务提供参考。
目前关于故障率时间预测的研究主要有人工神经网络[1-2](Artificial Neural Network,ANN)、支持向量机[3-4](Support Vector Machine,SVM)、ARMA模型预测法[5-6]等,但是ANN往往需要海量训练数据才能取得较理想的预测结果;而SVM的核函数比较复杂,需要引入多个参数;而像故障率这种非平稳的复杂序列,ARMA建模法的预测效果也十分有限。因此,针对含有多种未知因素相互影响的故障率时间序列,使用单一模型难以对其进行较高精度的预测。
在保留小波变换多分辨优势的基础上,经验模态分解[7](Empirical Mode Decomposition,EMD)作为一种自适应信号分解方法,解决了小波变换中分解尺度确定与小波基选取的问题。相关向量机(Relevance Vector Machine,RVM)已在解决小样本非线性回归估计等问题中展现出了良好的性能[8],灰色理论[9]又是处理“小样本”、“贫信息”的有效工具。本文通过EMD对故障率数据进行分解分析,再利用相关向量机与灰色模型预测,将各分量预测值叠加,得到最终结果。
1 经验模态分解
通过对复杂信号进行自适应多尺度分解,EMD算法逐步展现了其在非线性非平稳信号分析领域所特有的优势。EMD是将时间序列中不同尺度的波动或趋势逐级分解为一系列具有不同特征尺度的IMF分量。每个IMF分量具有一定的物理意义,分解结果突显了信号的局部特征,进一步分析即可准确把握原始信号的特征信息。
IMF必须具备下面两个条件:一是在整个时间范围内,局部极值点和过零点数目相同或至多相差一个;二是在任意时刻点,其上下包络线关于时间轴局部对称。若为包含n个数据的时间序列,其EMD的计算步骤为[7]:
① 确定X的所有极大值与极小值点,分别利用三次样条插值法拟合原序列的上包络线U1和下包络线L1,均与原序列长度相同,二者的平均为均值包络线M1:
M1(t)=[U1+V1]/2
(1)
② 令H1=X-M1,对H1重复步骤①直至其满足IMF条件,记C1=H1为X的第一个IMF分量。
③ 将R1=X-C1作为原始序列,重复上述步骤得到X的第2~m个IMF分量与一个余量(RF)R,结束筛选过程。最终原序列表示为:
(2)
从以上的过程可以看出,EMD分解后的IMF分量实质上包含了从高频到低频的不同频率成分,RF分量则代表了原始序列的平均趋势。
2 RVM 预测模型
RVM是一种新的非线性稀疏贝叶斯学习理论,其良好的泛化性能和较少的相关向量使其在预测领域逐步成为新热点,其回归模型原理[10]如下:

ti=y(xi,ω)+εi
(3)
式(3)中,样本Gaussian噪声εi~N(0,σ2)。类似于SVM的表达式,将上式用一系列核函数表示为:
(4)
式(4)中,ω=[ω0,ω1,…,ωN]T为权参数向量;K(·,·)为核函数。因此可以推断出p(ti|xi)=N(ti|y(xi,w),σ2),即ti满足ti~N(y(xi,w),σ2)。为方便表达,引入一个超参数β=σ-2,则整个训练样本数据组的似然函数表示为:
(5)
式(5)中,t=[t1,t2,…,tN]T;Φ∈RN×(N+1)是设计矩阵,定义为Φ=[φ(x1),φ(x2),…,φ(xN)]T,基函数向量为φ(xi)=[1,K(xi,x1),…,K(xi,xN)]T,i=1,2,…,N。

(6)
式(6)中,在超参数α=[α1,α2,…,αN]中的每个αj都相互独立且只与对应的权值ωj相关。利用式(5)和式(6),根据贝叶斯公式即可得到ω后验分布的表达式:
(7)
由于p(t|ω,β)和p(ω|α)均为Gaussian分布,二者乘积也同样满足该分布;而p(t|α,β)不含ω,可视作归一化系数,式(7)改写为:
p(ω|t,α,β)=N(ω|μ,∑)
(8)
式(8)中,均值矩阵μ和协方差矩阵∑分别为:
∑=(βΦTΦ+A)-1
(9)
μ=β∑ΦTt
(10)
其中,Α=diag(α0,α1,…,αN)。若要得到ω的后验分布,必须对两个影响参数β和αj进行优化,具体方法为最大化边缘似然函数p(t|α,β)。对p(t|α,β)等号两边取对数得到目标函数后,再分别对αj和β求偏导并令导数为0,得到两个参数的迭代计算公式为:
(11)
(12)
γj=1-αj∑jj
(13)

对RVM模型进行训练就是通过迭代计算不断更新μ和∑,直至参数收敛或达到最大迭代次数。
噪声方差σ2也通过迭代算法求得:
(14)
在超参数估计的收敛过程中,通过最大似然法得到αMP和σMP。若给定新的输入值x*,则相应预测输出的概率分布服从Gaussian分布:
(15)

y*=μTφ(x*)
(16)
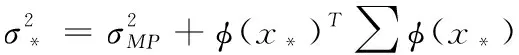
(17)
3 GM(1,1)预测模型
由于故障率变化趋势含有一些复杂的不确定及未知因素,而灰色模型对“贫信息、少数据”的时间序列具有良好的预测效果,因此本文采用GM(1,1)模型对EMD分解后的RF项进行预测。
设原始时间序列为[11]:
X(0)={x(0)(1),x(0)(2),…,x(0)(n)}
(18)
对X(0)做一次累加生成(1-Accumulated Generating Operation,即1-AGO)得到新序列X(1):
X(1)={x(1)(1),x(1)(2),…,x(1)(n)}
(19)
(20)
其差分形式(灰色微分方程)为:
x(0)(k)+vz(1)(k)=u
(21)
其中,z(1)(k)=[x(1)(k-1)+x(1)(k)]/2,k=2,3,…,n为GM(1,1)模型的背景值,Z(1)={z(1)(1),z(1)(2),…,z(1)(k)} 即为X(1)的紧邻均值序列。
微分方程中的参数向量为:
Q=[v,u]T
(22)
则待测参数的最小二乘解满足:
Q=(BTB)-1BTY
(23)
式(23)中:
(24)
Y=(x(0)(2),x(0)(3),…,x(0)(n))T
(25)
若规定x(1)(1)=x(0)(1),则GM(1,1)微分方程的解为:
(26)
还原得到原始序列的预测公式:
(27)
4 实例分析
以故障率预测的经典算例进行分析,选取波音757-700飞机的故障率数据为研究对象,数据采集来自文献[12],从1996年9月—1998年8月两年内共24个数据,如图1所示。
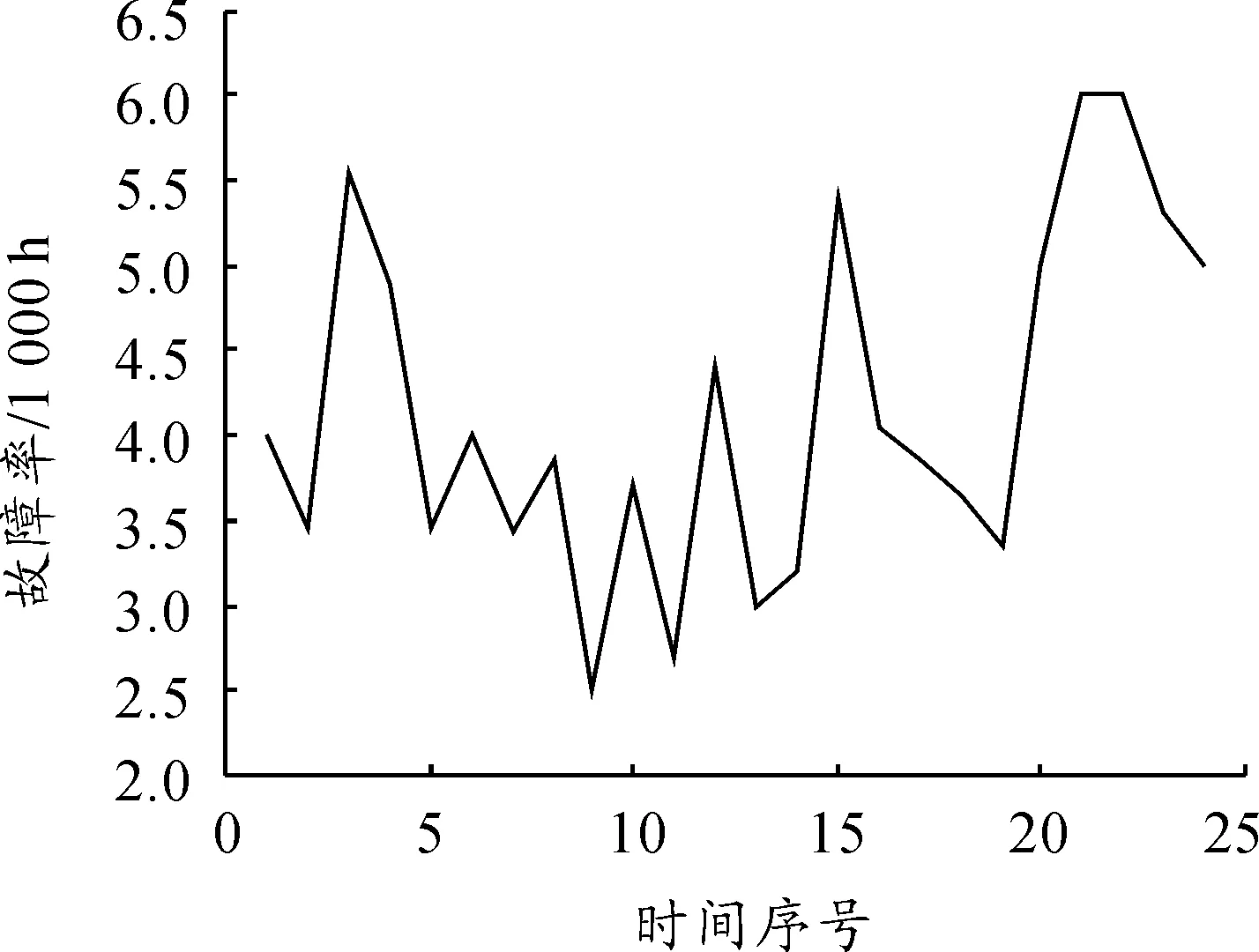
图1 故障率时间序列
为验证本文方法,通过EMD对前20个数据进行分解,结果如图2所示,最后4个故障率数据作为预测结果检验。通过图2可以看出故障率数据分解为1个RF项和3个IMF项,各分量更简单也更具各自的规律性,在此基础更易建模分析。

图2 故障率数据EMD分解结果
在利用GM(1,1)模型进行预测的过程中,不断加入新的预测信息向后预测,以提高精度,最后将各分量预测结果叠加得到故障率最终预测值。为将本文方法与已有方法进行对比分析,表1列出了本文方法与各模型的预测结果,其中,平均绝对百分比误差(MAPE)为预测性能评价指标,LS-SVM选取Gaussian核函数,核参数和正则化参数通过留一交叉验证法确定,嵌入维数为4。

表1 模型预测结果
从表1的预测结果可以看出,在与相关向量机和最小二乘支持向量机的预测结果对比中,本文方法的预测精度较高,说明EMD的分解是有效的,在其基础上对各分量利用RVM与GM(1,1)模型进行预测建模也符合故障率变化规律。
5 结论
实例分析表明,本文方法可以有效改善预测精度,具有工业应用前景,可以为维修决策人员提供前瞻性指导。
