长杆弹低速撞击刚性靶板过程中的过载特性研究
2018-07-31王耀羚卢玉斌
王耀羚,卢玉斌
(西南科技大学 制造过程测试技术教育部重点实验室, 四川 绵阳 621010)
侵彻是一个复杂过程,侵彻的研究由于其学科的特殊性,成为各国学者的研究热点之一[1]。侵彻过程是一个动态过程,其动态复杂性决定了侵彻过程中含有许多瞬变成分的非平稳信号,必须基于加速度计获取真实可靠的弹体侵彻过载,然后对所测过载数据进行系统分析,进而得到弹体过载变化规律,为精确有效计算出侵彻深度提供可靠的数据支持[2]。在侵彻研究中,根据侵彻速度不同,可分为高速、中速和低速侵彻,目前国内外学者研究的重点是高速和中速弹体的侵彻实验,而对于低速侵彻的研究较少。对于高速侵彻,国内外许多学者实验发现,加速度传感器采集的过载信号经过一次与二次积分后,得到的侵彻速度与侵彻深度和实际测量数据有较大的差值[3-4]。影响侵彻的因素许多,文献[5]发现长杆弹弹头形状对侵彻深度有较大影响。为了简化问题,分析导致加速度积分值与实际值偏差的原因,本研究以平头长杆弹低速撞击刚性墙为对象,研究不同速度下的加速度变化特性,对比分析加速度曲线的积分值与速度和位移,为中、高速侵彻时准确测量过载提出解决措施。
1 数值模拟模型
弹体垂直撞击刚性墙,长杆弹的长径比(L/d)为10,L=500 mm,d=50 mm。弹体的材料参数如表1所示。

表1 长杆弹材料参数
数值模拟主要研究在低速撞击情况下,不同加载速度时弹体的碰撞端和非碰撞端的加速度变化以及弹体的平均加速度变化,加载速度在3~10 m/s范围内。计算结果表明,在这几种极低的加载速度下,弹体均不会发生塑形形变,弹体变形在弹性阶段。
基于自由落体运动,将长杆弹从设定的高度释放,让其垂直自由下落并和靶板发生碰撞,从而产生不同的加载速度。在ABAQUS仿真过程中,将长杆弹和靶板定义为直接无间隙接触,如图1所示。

图1 长杆弹和靶板无间隙接触
本研究在数值模拟中采用六面体单元,设置单元类型时选择C3D8R实体单元进行模拟,在网格控制中选择中轴线算法(Medial axis)划分网格,这种算法能提高处理回转体模型的效率和精确度[6]。划分网格后总共有44 202个单元,48 640个节点,如图2所示。

图2 长杆弹的网格划分
2 理论加速度峰值计算
2.1 弹性应力波分析
通过应力波分析,长杆弹低速撞击刚性靶板的冲击不大,杆处于弹性变形下,应力波是一维线性弹性波。对线性弹性波而言,波速恒定,在均匀介质中传播其波形恒定不变。
根据牛顿第二定律,得到:
(1)
引入σ=P/A0,化简得到:
(2)
引入常数C,可得出:
(3)
杆处于弹性形变时,应力和应变满足Hooke定律,其本构关系为:
σ=Eε
(4)
式中:E为杨氏模量,由此得出常数C仅由材料本身属性ρ0和E所决定。
(5)
由此可知杆中弹性应力波波速与外界条件无关。代入材料参数得到弹性应力波的波速C0=5 190 m/s。
弹性波在有限长度杆中传播,波长λ近似为长杆L,有λ=L=0.5 m,撞击产生的应力波在杆中来回振荡,由此得到波形脉宽的表达式:
(6)
代入数据计算,得出T=96 μs。
2.2 冲击脉冲理论分析
设长杆弹自由下落的高度为h1,根据牛顿第二定律可得,弹体与靶板碰撞瞬间其速度为:
(7)
碰撞产生的反作用力使长杆弹反弹,假设反弹高度为h2,则碰撞后反弹的速度为:
(8)
若将上述公式作为边界条件,则碰撞过程中长杆弹的速度变化可以表示为:
(9)
其中T为响应波形的脉宽。
将式(3)进行一次微分运算,得到碰撞过程中长杆弹的加速度变化,表示为:
(10)
由此可以得到碰撞过程中的加速度峰值为:
(11)
式(11)是计算碰撞过程中加速度峰值的基本公式[7]。 给定3 m/s、5 m/s、7 m/s、8 m/s、9 m/s和10 m/s 6种不同的初速度。由于长杆弹以这6种初速度垂直碰撞时,其反弹高度较低,将整个过程简化,h2赋值为0,并设定波形脉宽T=96 μs[8]。则碰撞过程中加速度峰值的公式可以简化为:
3 数值模拟结果
3.1 频率分析
采样频率f,也称为采样率,定义了从连续信号中提取并组成离散信号的采样个数,它用赫兹(Hz)表示。在动态分析中,离散信号是由连续信号采样得到的信号。选择合适的采样频率既能保证信号精确度,也能控制数值模拟计算时间。
本文数值模拟选取f=2 MHz 、1.5 MHz和1 MHz三个不同频率作为分析参数,对比采用不同频率时信号的精确度。研究发现采样频率和初速度无关,因此选取v=3 m/s时不同频率下的平均加速度进行对比,如图3所示。
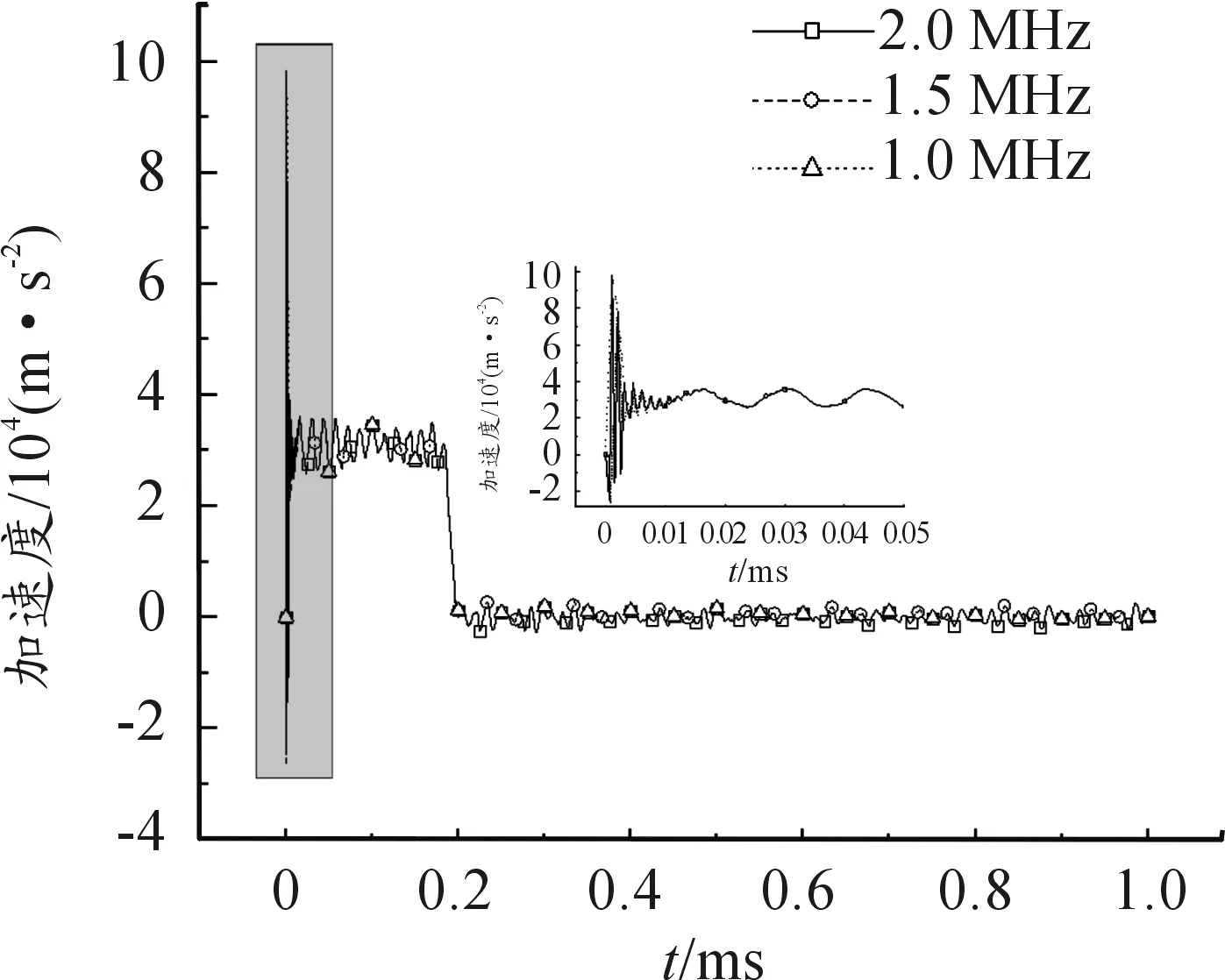
图3 不同频率下3 m/s时的平均加速度
从图3可以看出,不同频率的平均加速度曲线差别不大,在0.05 ms范围内,不同频率下的信号不同。采样频率高时获得的数据更精确,当f=1 MHz时只存在一个波峰;f=1.5 MHz时,波峰波谷各有两个;当f=2 MHz时,波峰波谷各有3个。说明采样频率取2 MHz时比其他两个频率能采集到更完整的数据信号。数值模拟计算时间和计算规模受计算机运算能力影响,因此保证数据的精确和降低计算时间选择2 MHz作为采样频率。
3.2 平均加速度分析
靶板为刚体,仅研究平头长杆弹碰撞时弹体的加速度变化情况。基于数值模拟获得了上述6种不同初速度加载时的弹体平均加速度峰值。图4中A1是数值模拟中长杆弹撞击刚性靶板的平均加速度峰值,A是理论加速度峰值。模拟加速度峰值和理论值有相同的变化趋势,均随着侵彻速度的增加而增加。对比发现理论加速度峰值和模拟加速 度峰值有22.5%的偏差。这可能是依据理论公式计算时,把h2取为0,实际上数值模拟时弹体发生了反弹,并且反弹高度会随着初速度的增大而增大。模拟值和理论值在相同数量级,误差在许可范围内,因此本文数值模拟的准确性是可接受的[9]。
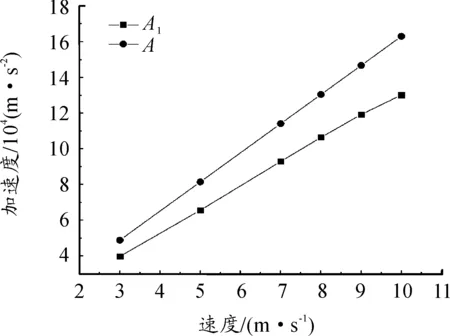
图4 理论加速度峰值A和模拟加速度峰值A1的比较
当加载速度为3 m/s时,长杆弹的平均加速度曲线如图5所示。从图5中可以观察到,加速度在30 000 m/s2处振荡。在t=0.196 ms时,长杆弹开始反弹,脱离靶板之后由牛顿第二定律可知,随着弹体离靶,长杆弹不受靶板的反作用力作用, 然而由于弹体离靶后,还有应力波在弹体中来回传播,所以加速度在零附近振荡。对比速度差为2 m/s(3 m/s、5 m/s、7 m/s、9 m/s)撞击靶板的数据,发现相邻两速度的加速度峰值最大相差26 000 m/s2,增长率随着速度的增大而减小,从66.7%降低到28%,如图6所示。对比速度差为 1 m/s(7 m/s、8 m/s、9 m/s、10 m/s)撞击靶板的数据,发现相邻两速度的加速度峰值最大相差13 000 m/s2,增长率同样随着速度的增大而减小,从14.5%减小到9.1%,如图7所示。
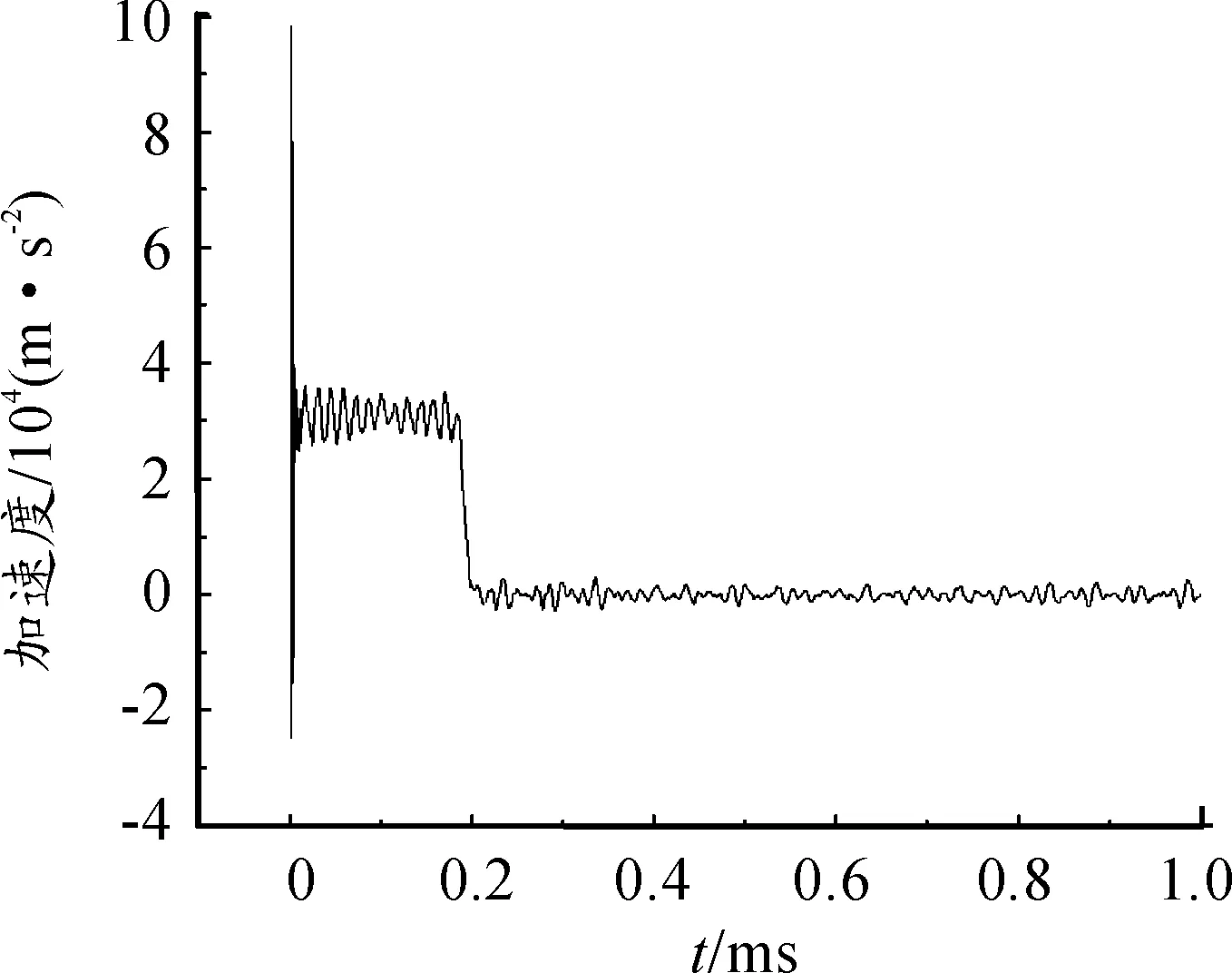
图5 速度为3 m/s时的平均加速度
分析数据可以发现,加速度波动在一个水平线上,当v=3 m/s时,加速度值在30 000 m/s2处波动;v=5 m/s时,加速度值在50 000 m/s2处波动;当v=7 m/s时,加速度值在 70 000 m/s2处波动;以此类推,当v=8、9、10 m/s时,加速度值在80 000 m/s2、90 000 m/s2、100 000 m/s2处波动。由此可见长杆弹低速撞击刚性靶板,在弹体材料的弹性阶段,弹体平均加速度a满足:
a=105v
(13)
式中v为加载初速度。
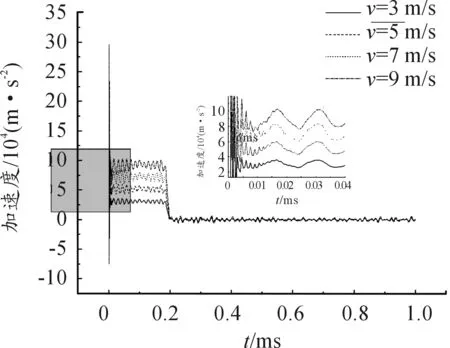
图6 速度差为2 m/s的平均加速度
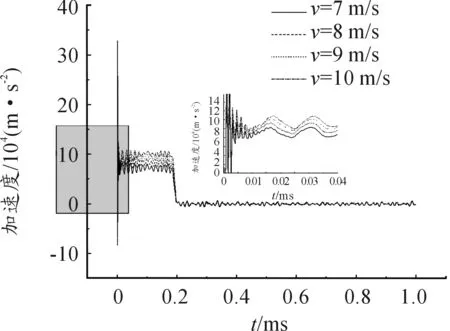
图7 速度差为1 m/s的平均加速度
3.3 节点加速度分析
本文数值模拟模型中弹体撞击端中心节点为N28,非撞击端中心节点为N48364。
对比两端中心节点的加速度峰值,结论是加载速度越大,撞击端与非撞击端加速度的比值λ越大。当v=3 m/s时,比值λ为7.7;当v为10 m/s时,比值λ为15。不同加载速度下,λ的变化曲线如图8所示。
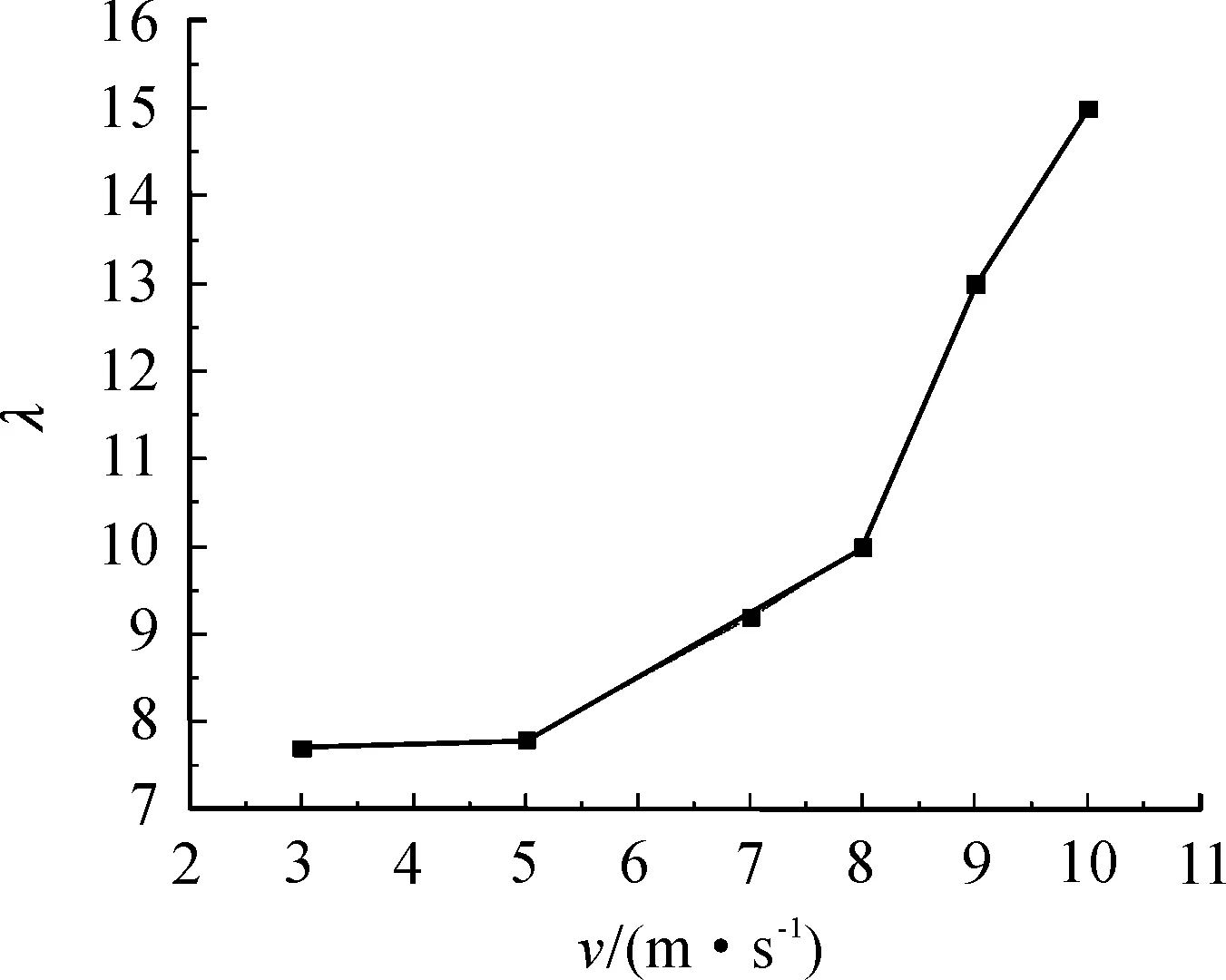
图8 加速度峰值比
从图8可以看出,低速撞击下,撞击端加速度至少是非撞击端的7.7倍,随着加载速度的递增,λ值迅速增大,这与文献[10]结果一致。
中心节点N28处加速度一次积分后的速度曲线和撞击速度曲线对比如图9所示,图10所示为加速度二次积分后的位移和靶板形变的对比图。其中“v*”代表加速度积分后得到的数据,“v”表示未积分的数据。发现节点N28的加速度积分得到的速度与撞击速度之间的差异以及积分位移值和靶板形变之间的差异,均随着加载初速度的增加而减小。
非撞击端中心节点N48364处加速度积分后的速度和撞击速度的对比如图11所示,图12所示为加速度二次积分后的位移和靶板形变对比。“v*”代表加速度积分后得到的数据,“v”表示未积分的数据。
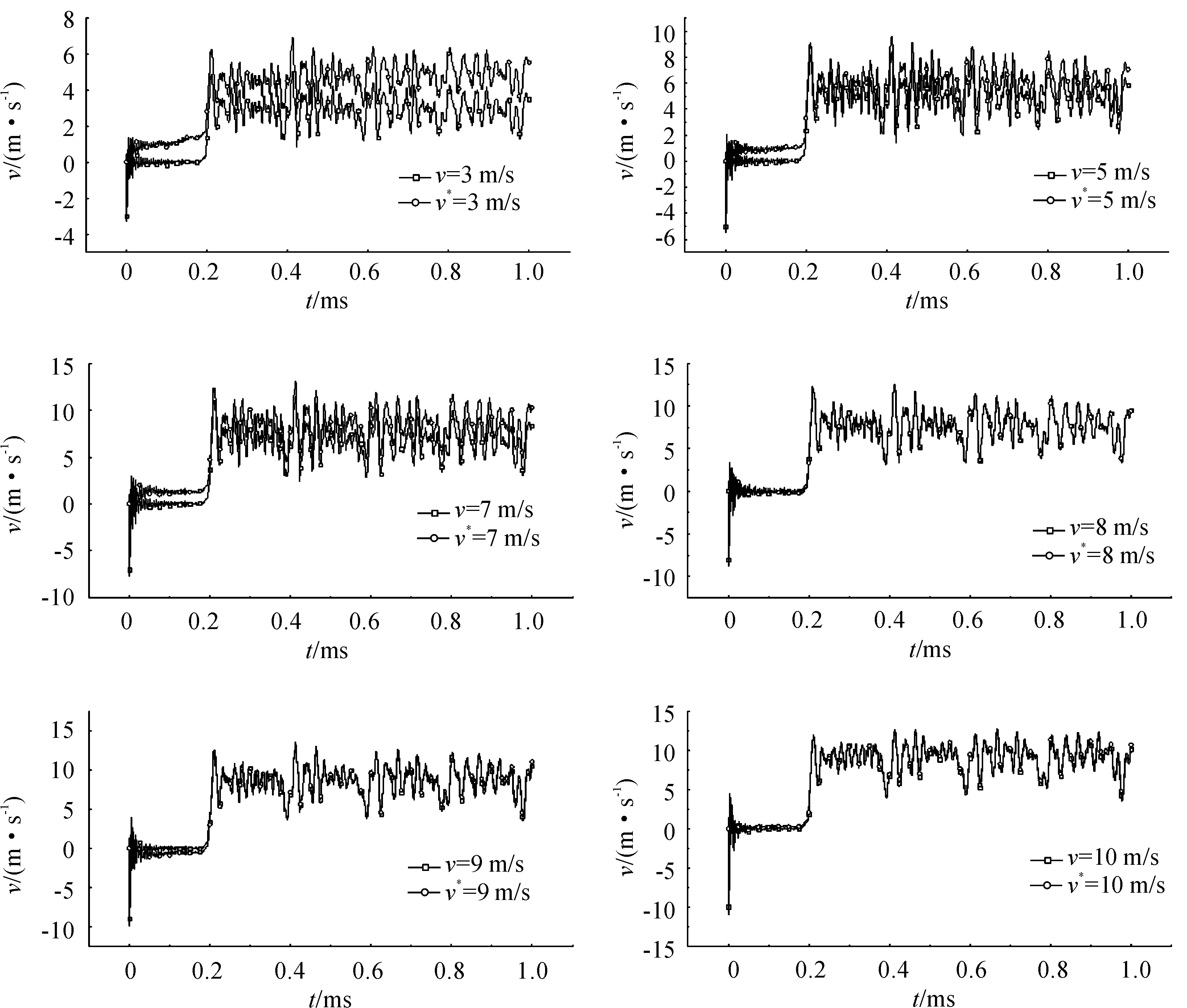
图9 节点N28加速度积分后速度和撞击速度
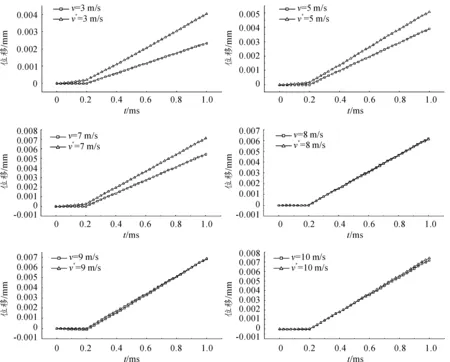
图10 节点N28加速度积分后位移和靶板形变
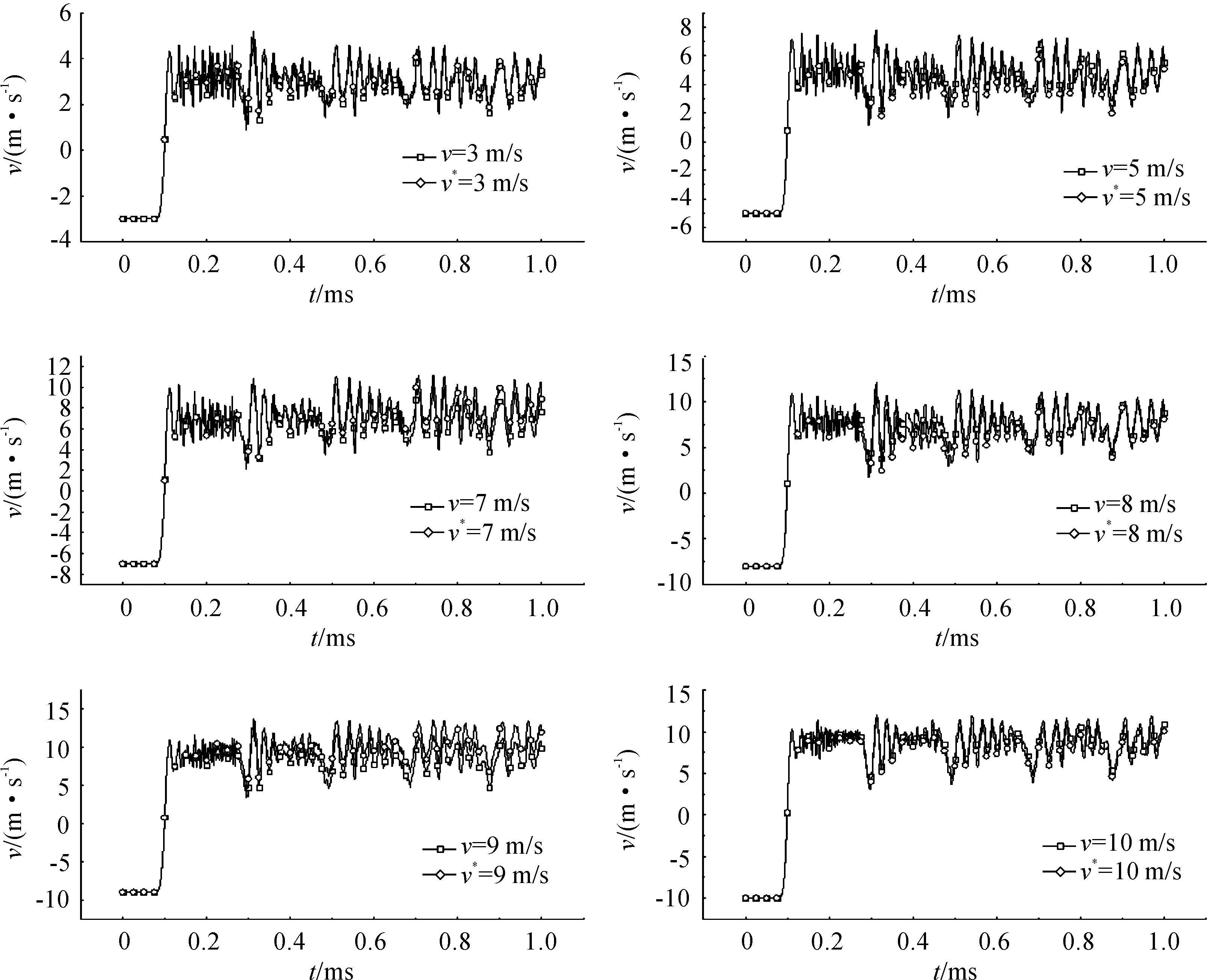
图11 节点N48364加速度积分后速度和撞击速度
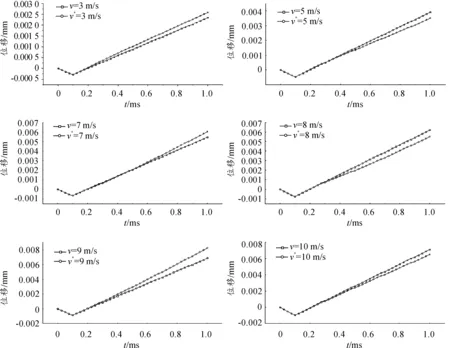
图12 节点N48364加速度积分后位移和靶板形变
发现节点N48364加速度积分后得到的速度以及位移与加载初速度和靶板形变均能较好地吻合。说明在低速碰撞情况下,弹尾安装加速度传感器,采集的信号经过一次和二次积分后,得到的速度和位移应能很好的符合实际测量值,也就意味着此时所测量的加速度信号是准确可用的。由此可以推测,在中、高速侵彻下,过载信号积分值与实际值之间有较大偏差的原因很有可能是因弹体在侵彻过程产生的应力波严重影响了过载信号测量的准确性,为了提高过载信号测量的准确性,应采取措施降低或隔离应力波的影响,如在过载记录仪中引入泡沫材料。
4 结论
1) 在长杆弹材料的弹性极限范围内,低速撞击过程中的平均加速度值随加载速度的增加而提高,端面节点的加速度峰值亦随加载速度的增大而增大,加速度峰值提高了一个量级。通过本次数值模拟实验,为今后进行侵彻实验提供了一定的理论支持,为加速度传感器的安装提供可参考的指导意义。
2) 低速碰撞情况下加速度信号经一次和二次积分后,得到的速度和位移与实际对应数据的差值很小。
