基于核相关滤波器和多检测器的尺度自适应视觉跟踪∗

赵乾臣 金 忠

（南京理工大学计算机科学与工程学院 南京 210094）

1 引言

目标跟踪是计算机视觉中最具挑战性的问题之一，它在许多应用中起着至关重要的作用，如人机交互、监控和机器人。然而，目标跟踪受诸多因素（如光照变化、部分遮挡、背景干扰和形变等）的制约。在本文中，我们提出了一种方法来缓解这些问题。

在早期的跟踪方法中，通常通过颜色直方图［1～3］，局部信息［4～5］来对目标进行建模。然而不稳定性、弱鲁棒性和低鉴别性成了该类模型的缺点。所以，在过去的十年中，研究人员将更多的关注放在了基于更具有代表性的目标特征如 HOG［6～7］、更复杂的颜色特征如颜色属性［8］以及相关滤波器［9～10］的跟踪方法上。相比早期的跟踪算法的性能，这些跟踪器在最近的数据库上［11］获得了很不错的表现。

从理论上来讲，一个非常具有挑战性的因素是我们希望在满足实时性要求的前提下，从原始图像中获得尽可能多的负样本。因此为了满足实时跟踪的要求，现在大部分的跟踪器［12～16］通过每一帧在目标周围随机选取适量的样本来权衡实时性和足够多样本这两个需求。

最近，基于鉴别性相关滤波器的方法［6～10，17］已经成功地应用在了跟踪领域。这些算法通过循环滑动窗口对给定目标周围进行采样，从而生成一组训练样本，并基于此训练样本来学习并得到一个相关滤波器。因为采样的特殊性，使得算法可以有效地利用快速傅里叶变换来加速滤波器的训练和检测，从而能在满足实时性的同时，通过大量样本来训练得到一个性能不错的跟踪器。

相比于其它跟踪算法，在本文中我们提出一种基于目标轮廓信息和灰度信息的尺度检测器来适应目标尺度的变化。此外，我们建立了一个多检测器框架来克服由于光照变化和遮挡等引起的模型漂移现象。最后我们在最近的基准数据集上进行评估来表明该方法相对于其它跟踪算法的优势。

2 核相关性滤波器

最近，许多基于核相关性滤波器的跟踪算法［6，8～10，18］通过在大小为 M × N 的目标区域 X 训练分类器ω。其中，通过循环位移而生成所有的训练样本 Xm，n，m∈[0，M-1]，n∈[0，N-1]的类别y(m，n)标签服从高斯分布：

其中ϕ是核函数空间，λ是正则化参数（λ≥0）。由于样本标签是连续变化的值，所以采用基于正则化最小二乘法来（RLS）训练分类器是正则风险最小化的解。其中系数α为

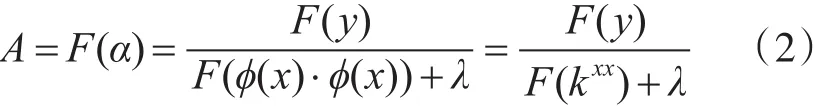
其中F为离散傅里叶变换，y是大小为M×N的样本标签矩阵。kxx是核函数矩阵K的第一行。跟踪任务是计算下一帧图像中提取的各测试样本的响应值：

其中F-1为傅里叶逆变换，x为前一帧学习到的目标模型，⊙是点积，Z是在当前帧提取到大小为M×N的图像特征。

我们采用高斯核函数kxx′=exp(-‖‖x-x′2σ2)来计算 kxx′=ϕ(x)·ϕ(x′)，因此式（3）中基于多通道特征的kxz可以表示为

为了提高对光照变化、遮挡以及形变等因素的鲁棒性，我们需要实时地更新目标模型Rc：

其中γ是目标模型学习率，f是当前帧的索引。

3 尺度检测

在目标跟踪期间，如果目标尺度发生变化，尤其是当目标变大的时候，我们便不能够准确地提取目标特征。所以我们提出一种基于目标灰度直方图以及边缘信息的尺度估计算法，如图1所示。

图1 尺度检测流程图

当我们获得当前帧目标的位置以后，我们通过提取目标的灰度信息以及拉普拉斯边缘检测信息来构建目标的尺度金字塔。令M×N为目标大小，P为尺度金字塔S的层数，S={scale_stepP2-n|n∈[0， P-1]}，对于任意 s∈S ，我们在目标位置提取大小为 sM×sN的感兴趣区域 Js并放缩到M×N，然后计算相应的灰度直方图ηhist和轮廓特征 ηtmpl。

将轮廓特征ηtmpl转变为一维向量并与灰度信息串连得到尺度Sn下最终的训练样本xn，因此我们可以通过一组训练样本X={xn| n ∈[0， P-1]} 来训练尺度模型：

其中，X*是X的共轭，Y是所有训练样本标签所组成的1×P的矩阵，训练样本标签服从一维高斯分布：

我们可以通过训练得到的模型对当前帧进行尺度估计，不同尺度下的样本的相应可以表示为

其中X′是当前帧不同尺度下提取到的测试样本集合，ŷ为所有测试样本的响应值。因此，响应值最大的位置便是当前帧目标相对于上一次尺度检测结果的最优尺度标签ind。

考虑到在相邻两帧之间目标的尺度变换很小，因此在实验部分我们每过φ帧进行一次尺度更新。此外，为了克服光照变化、遮挡等对尺度估计的干扰，我们提出了一个尺度更新判别机制：

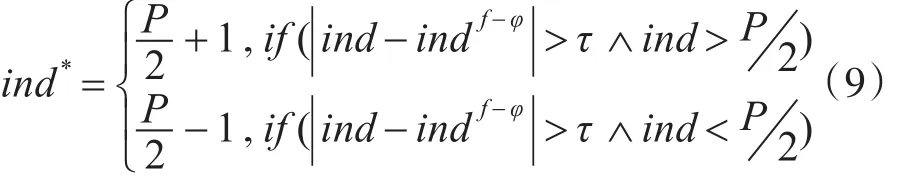
其中 f是当前帧的索引，τ是控制前后两次尺度变换程度的参数。因此，最终目标相对于初始化时的尺度可以被表示为

其中ℑ是前一次尺度，T控制目标尺度变化最小值。

为了提高尺度检测稳定性，我们在尺度检测后以学习率γs来更新尺度模型Rs：

4 多检测器框架

在长时间目标跟踪下，由于光照变化和遮挡等因素导致的跟踪失败是视觉跟踪里经常出现的问题，当目标跟踪丢失以后，为了使得当目标重新进入检测范围内时能被重新跟踪，我们提出一个基于多个历史检测器共同检测框架来改善长期跟踪效果。

视觉跟踪通过一个感兴趣区域来初始化，因此通过第一帧训练得到的检测器鉴别性最好，所以我们将该检测器ψ1长期驻留在多检测器组中，此外我们每过ζ帧存储当前的检测器ψi直至检测器总数达到N，因此，最终的多检测器可以被表示为M={ψ1，…，ψN}。

在随后的视频序列中，除了通过前一帧训练得到的检测器，多检测器组中的每一个检测器都会给出独立的检测结果vψi，即相关度最高的样本的回归值。最终可通过不同检测器在各自检测阶段的综合表现来决定选取哪一个检测结果作为最终的跟踪结果：

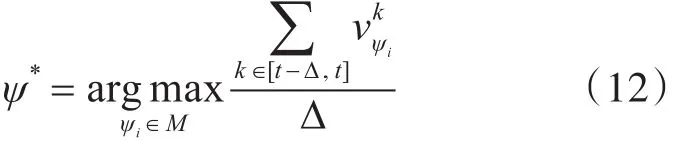
其中k是当前帧的索引，Δ是检测器ψi已经检测过的帧数，ψ*是最终采用的最优检测器。

此外，为了适应长期跟踪面临的环境变化以及目标自身的变化，当 ||M ＞N时，除了长期驻留的检测器ψ1，我们将每隔ζ帧来更新一个历史保留的检测器。

5 实验结果分析

5.1 算法及实验参数

在本实验中，我们使用轮廓特征HOG［7］和颜色特征CN［8］作为目标的多通道特征，此外，式（2）中的正则项系数 λ=10-4，式（3）中的高斯核带宽σ=0.5，式（5）中学习率为0.008。在尺度检测阶段，尺度金字塔层数为P=27，尺度步长为1.05，检测频率 φ=5，式（6）中正则项系数 λ=10-3，式（7）中的尺度带宽为 s= P 4，式（11）中学习率为0.0015。多检测器框架中N=5，ζ=100。

此外，考虑到对于视频中较小目标而言，一方面，可以认为目标距离相机比较远，所以导致目标对于相机的移动或者晃动非常敏感。另一方面，通过较小目标循环位移所生成的样本数量不能够很好地训练出一个较优的检测器。基于此，在本实验中，我们将目标初始化大小考虑进来，面积大于5000像素的目标的搜索窗口为目标大小的1.53倍，反之则为目标大小的1.8倍。

该跟踪算法的流程图如下：

输入：通过给定窗口初始化目标C0输出：t时刻目标位置和尺度大小 Ct=(x̂t，ŷt，ŝt)步骤1：根据上一帧检测的位置对当前帧感兴趣区域提取特征。

步骤2：通过上一帧训练好的模型和式（3）来检测目标最新位置。

步骤3：如果存储的历史检测器数量 ||M=N，则每一个检测器分别给出当前帧目标最新位置(xt，yt)，并通过式（12）选取最佳检测结果。

步骤4：如果 mod(t，ϕ)=0，则构建目标尺度金字塔，并通过上一次训练得到的尺度检测器与式（8），（9）和（10）来估计当前尺度 ŝ。

步骤5：使用式（2）和式（5）来更新目标外观模型；使用式（6）和（11）更新尺度模型。

步骤6：如果 mod(t，ζ)=0，则将当前检测器保存到多检测器组中或者用当前检测器更新检测器组的一个检测器。

5.2 总体实验结果

本实验环境配置如下：Visual Studio2013，Inter I5-2410M 2.30GHz CPU，4GB内存。

我们在基准数据库OTB13上与其它目标跟踪领域经典算法 KCF［7］，Struck［16］，CSK［10］，CN［8］和TLD［13］进行比较，如表1所示。

表1 本算法与其它经典算法在跟踪精度DP、重叠精度OS以及平均中心误差CLE上的对比

表2为本文所提出的算法与基准KCF算法的运行速度对比结果。从对比结果可知，由于增加了尺度检测以及多历史检测器跟踪模块，使得运行速度只有原来的36%，但处理速度仍然满足实时性的要求（每秒处理帧数在15帧～20帧都可视为实时性跟踪）。

表2 与基准KCF算法运行速度对比

图2给出了上述算法在OTB13数据库上的跟踪精度和重叠精度。对于跟踪精度，当阈值选取20像素时，本文算法比KCF高9.2%。对于重叠精度，当阈值选取0.5时，本文算法结果为70.6%。

图2 本文算法与其它经典算法在OTB13数据库上的跟踪精度与重叠精度对比

5.3 基于属性的评估实验

我们对于OTB13数据库中50个测试视频序列进行分类评估，按照跟踪属性的不同可将视频序列分为11类。在此，我们给出其中6类属性的跟踪精度。从图3中可知，以20像素为阈值，对于具有背景干扰、目标形变、光照变化以及平面外旋转的测试序列，KCF的跟踪准确率分别为70.8%、78.5%、68.6%和72.0%，而本文提出的跟踪算法的跟踪准确率分别为77.3%、83.0%、77.9%和82.3%。此外，对于具有快速运动和尺度变化性质的测试序列，相比于Struck的62.0%和64.0%，我们的跟踪算法取得了69.8%和77.2%的跟踪准确率。

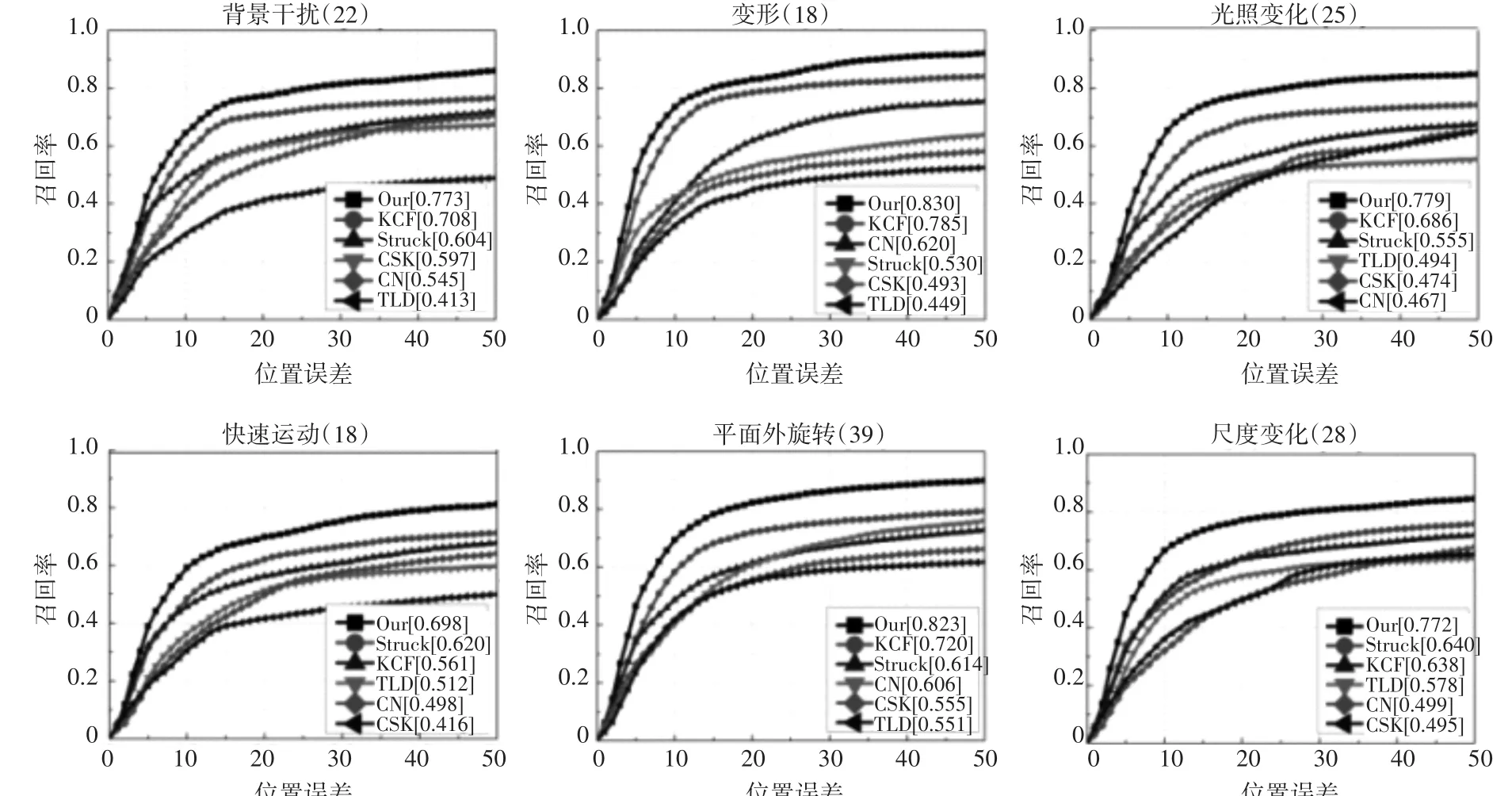
图3 本文算法与其它经典算法在六个跟踪属性上跟踪精度对比

5.4 尺度检测实验

为验证尺度检测的有效性，我们给出了本文算法以及五种经典跟踪算法在9个测试序列上的重合度，如表3所示。可以看出，本文提出的算法在这些测试序列上都取得了最高的重合度。一方面，通过提取目标的形状和灰度特征训练尺度检测器要比传统的模板匹配等方法要有效。另一方面，尺度更新判别机制也能够保证在出现错误判断的情况下，目标尺度变化也保持较为平稳的变化，保证了跟踪算法整体的稳定性。稳定的尺度更新使得在目标跟踪过程中能够提取更精准的目标特征来训练跟踪器，从而也提高了跟踪算法的准确度。

表3 本文算法与其它经典算法在9个测试序列上重合度对比（%）

5.5 多检测器模型更正实验

为验证多检测器对目标丢失后的更正效果，本文使用跟踪目标在运动过程中受到遮挡的视频序列进行测试。实验结果如图4所示，图4（a）为目标跟踪结果对比，图4（b）是对应帧的多个检测器的响应值比较。如第377帧上的跟踪结果以及响应值所示，当目标状态由丢失变为重新出现后，第二个历史检测器取得最高的响应值，因此，我们选取第二个历史检测器的跟踪结果，并且待跟踪目标模型被第二个历史检测器所保存的目标模型所替换，达到模型更正的效果，否则，若选取灰色框的跟踪结果，则将会出现目标跟踪丢失现象并且无法找回。

图4 多检测器实验结果

此外，我们从OTB13数据集上选取了两组长期跟踪的视频序列Lemming和Liquor，并比较了本文提出的算法与其它经典跟踪算法的平均中心误差CLE。如图5所示，对于Lemming视频序列，当目标发生遮挡、旋转等情况后，学习到的目标模型发生变化，使得其它经典算法的跟踪结果与标定结果均有较大的误差，而本文提出的多检测器框架，在同一时刻，会有多个检测器给出各自的检测结果，并从中选取最优结果作为最终的跟踪结果。因此，即便前一帧所训练得到的目标模型发生漂移，多个历史检测器也能有效地更正跟踪目标。对于Liquor视频序列，在900帧～1200帧之间，由于遮挡以及背景干扰等因素的影响，所有跟踪算法均出现了跟踪丢失现象，各自跟踪结果的平均中心误差均较大。而当目标重新进入检测区域时，相对于基准跟踪算法KCF，本文提出的多检测器框架能够及时更正跟踪目标模型，使得在后续的跟踪中，能够继续准确地进行目标跟踪任务，跟踪结果的平均中心误差也重新降低到可接受的范围内，而其它算法的跟踪结果仍未有较好的改善。

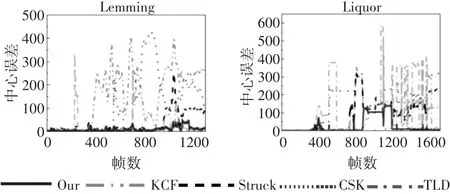
图5 本文算法与其它跟踪算法在两组测试序列上的平均中心误差对比

5.6 定量分析实验

如图6所示，我们在八个视频序列上比较本文提出的算法与KCF，CSK，TLD和Struck的跟踪结果。由于KCF提取目标的HOG特征来对目标进行建模，因此对于快速移动和目标形变的测试序列比原始算法CSK要更加鲁棒。但是当目标发生严重遮挡（如Lemming和Liquor）时会出现模型漂移的现象。此外，由于KCF只应用了目标的轮廓特征这一单一特征，使得其不能很好地处理具有严重背景干扰的视频序列（如Bolt和Soccer）。CSK跟踪算法是基于核相关性滤波器这一理论的经典算法，由于只采用了图像的灰度信息，所以对于一些跟踪难度低的视频序列（如Dog1）能保持最快的检测速度和不错的跟踪精度，但对于具有背景干扰、形变等（如Soccer和Freeman1）特性的目标跟踪效果一般。对于Struck跟踪算法而言，由于单一的分类器，以及不能够适应目标的变化，导致其在旋转、背景干扰或者严重遮挡方面（如Jogging和Soccer）表现不佳。与Struck不同，TLD跟踪算法可以实时地学习目标最新的模型并能够适应目标的尺度变化，但是对于快速移动和目标形变鲁棒性较弱（如Bolt和Freeman1）。此外，TLD容易受遮挡、光照变化的干扰，使得不能够平稳地进行尺度更新。

图6 本文算法与其它跟踪算法在八个测试序列上的跟踪结果对比（自上而下为Bolt，Dog1，Doll，Freeman1，Jogging，Lemming，Liquor，Soccer）

综上所述，本文提出的跟踪算法在跟踪精度和尺度估计方面均有较好的表现，一方面在HOG特征的基础上，融合了CN颜色特征提高了算法对复杂环境的鲁棒性。另一方面，本文提出的基于灰度直方图和轮廓信息的尺度检测算法能够很好地适应目标尺度的变化，并且较其他尺度检测算法更稳定（如Dog1、Doll、Freeman1和Soccer）。对于长期跟踪的视频序列（Lemming和Liquor），本文提出的多检测器更正框架使得能够在跟踪丢失的情形下，当目标重新进入检测区域时，目标模型能够被重新更正。

6 结语

本文中，我们在基于核相关性滤波理论的基础上，使用目标的灰度直方图以及轮廓信息来训练尺度检测器以适应目标在长期跟踪过程中的尺度变化。此外，对于长期跟踪的目标，由于严重遮挡或者背景干扰等因素导致跟踪丢失后，当目标重新进入检测区域时，我们提出的多检测器跟踪框架能够重新更正目标模型。从在OTB13数据库实验结果可以看出，在满足实时性的基础上，本文提出的算法相比于其它经典算法更加鲁棒与稳定。