基于有穷论域下区间时序逻辑的模型检测研究∗
2018-07-31李超
李 超
(西安邮电大学计算机学院 西安 710061)
1 引言
模型检测[1~2]是形式化验证的一种重要方法,它以自动化的验证技术克服了演绎证明的局限性得到了人们的青睐。区间时序逻辑(Interval Tem⁃poral Logic,ITL)是线性时序逻辑的一个重要分支,在模型检测中有很大的利用价值。模型检测可以帮助人们自动地验证系统属性的正确性,从而从根本上减少了系统的错误,降低了系统维护的成本。模型检测是建立在逻辑的可判定性的基础上,文献[3]已经证明了有穷论域下区间时序逻辑的可判定性,但是目前基于区间时序逻辑的模型检测工具寥寥无几,而现有的区间时序逻辑的模型检测工具在建模和性质描述上都有很大的不便利性,给用户的使用带来了极大的不便。本文在有穷论域下区间时序逻辑的判定性的基础上利用自动机技术给出了一个模型检测工具的设计及实现。
2 概念
2.1 模型检测
在计算机科学中,模型检测指的是给定一个系统模型,彻底地、自动地检查该模型是否符合某个给定的要求。一般的,在软件或者硬件系统中,给定的要求一般包含像无死锁的这样的安全需求和一些可能导致系统崩溃的关键状态。模型检测是一种自动化地验证有穷状态系统的属性正确性的技术。
为了利用算法解决模型检测的问题,系统模型和要求说明都必须用精确的数学语言来表达。为达到这样的目的,模型检测被表述为一个逻辑运算过程,也就是检验一个给定的系统模型是否满足某个逻辑公式。一个简单的模型检测例子是验证一个系统是否满足一个由逻辑公式描述的性质。如图1所示。
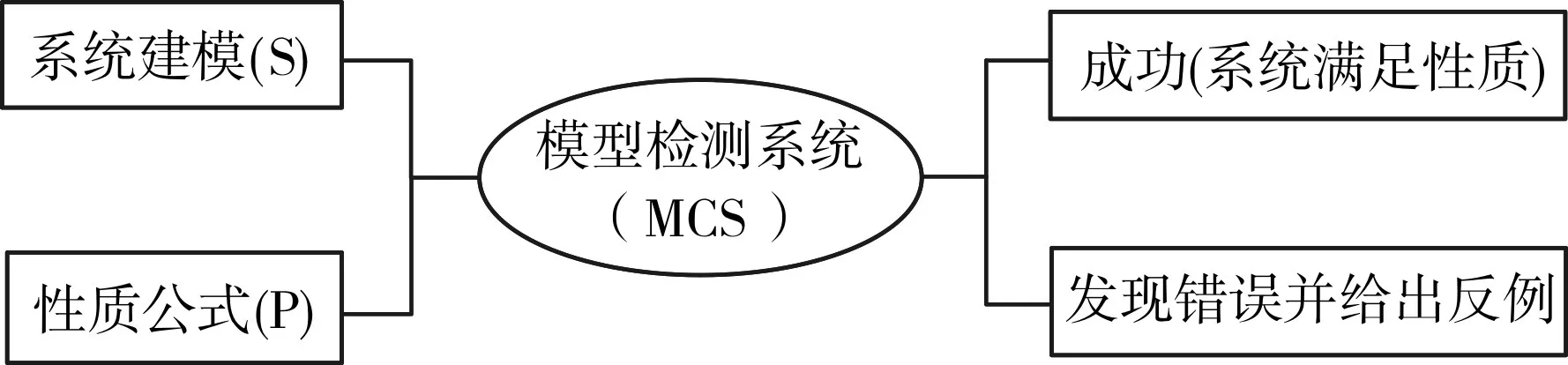
图1 模型检测系统
2.2 区间时序逻辑
时序逻辑(Temporal Logic,TL)[4~5]的思想是:在一个模型中,公式的真与假不是静态的,在一个包含多个状态的模型中一个公式可以在某些状态下满足且在其他状态下不满足。时序逻辑在形式化验证中已经有了重要的应用,即它被用来表达硬件和软件系统的要求。比如,我们可能有这样的要求“不管什么时候做出请求,对资源的获取最终会被准许,但是不会同时允许两个请求者同时获得资源”,这样的一个描述可以很方便地用时序逻辑表达。
区间时序逻辑(Interval Temporal Logic,ITL)[6~7]同样是一种线性时序逻辑,它可以表达在时间区间上的命题逻辑和一阶逻辑,它有能力表达顺序和并行的组合情况。区间时序逻辑处理的是有穷的状态序列而不是无穷的序列。区间时序逻辑在计算机科学、人工智能、语言学领域中都得到应用。
定义1 区间时序逻辑的项e和公式P的定义由下面BNF给出:
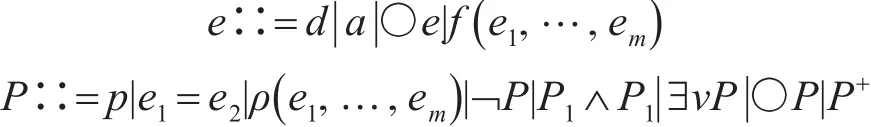
其中,d∈D为常量,D为任何数据类型的有穷论域;a∈V是静态变量;x∈V是动态变量;v∈V是任意的静态变量或者动态变量,其中V为静态变量和动态变量的可数集合;p∈Prop为原子命题,其中Prop是原子命题的可数集合;f(e1,…,em)与 ρ(e1,…,em)分别表示 D上带有m元参数的函数与谓词;(N ext),+(C hop Plus)是原始时态操作符。
在ITL的语法定义中,常量d、函数 f及谓词ρ均与其所在论域D是相关的。例如true和false是布尔论域B中的两个常量;0,1,2,…是非负整数集合 N0(N0为非负整数集合)上的常量,+,-,×,∕是 N0上的函数,且 <,≤,>,≥ 是 N0上的谓词。
定义3 (基本ITL公式)基本ITL(Basic ITL,BITL)公式是满足下列三个条件的公式:
1)公式中不包含任何时态项;
2)公式中所有等词均形如v=d,其中v∈V为变量,d∈D为常量;
3)公式中不包含任何除等词(=)之外的其他原始谓词。
2.3 自动机
自动机[7]理论已经在很多领域有广泛的应用,同时它在模型检测中也起着至关重要的作用。有穷自动机可以被看作是一个带有有穷输入的设备,而它可以接受或者拒绝这个输入。这个设备会随着它从左到右读取输入而变化自己的状态。在有穷自动机处理完成一个输入后可以得到的仅是最终它到达的状态的种类,也就是接受或者不接受。有穷自动机只接受有穷行为的特性不能满足一些系统的需求。Büchi自动机[9~10]将有穷自动机扩展到可以接受无穷输入,当Büchi自动机的一次执行无限到达某个终结状态,那么它就接受一个无穷输入。Büchi自动机是瑞士数学家Julius Richard Büchi在1962年发明的。目前Büchi自动机已经成功应用到基于 LTL[11~12]的模型检测工具 SPIN[13~14]中,但由于Büchi自动机本身只能接受无穷行为,却不能接受有穷行为,故在验证时存在缺陷。完全有穷自动机(Complete Finite Automata,CFA)结合了有穷自动机和Muller自动机[15~16]的优点,能够接受有穷行为和无穷行为。
3 模型检测关键技术研究
3.1 模型检测流程
ITL模型检测工具的工作流程图如图2所示,首先需要构造出描述系统模型的系统自动机(Sys_CFA)和描述性质的性质自动机(P_CFA),然后对P_CFA进行自动机的求反运算得到性质非自动机~P_CFA,最后对系统自动机和性质非自动机求交判断系统是否满足性质。

图2 模型检测流程图
3.2 利用自动机进行模型检测
定义4(完全有穷自动机)一个完全有穷自动 机 (CFA) 定 义 为 一 个 六 元 组A={ }
Σ,Q,δ,I,F,C ,其中:Σ 为字母表;Q 表示状态集合;δ:Q×Σ→2Q是状态迁移集合;I∈Q表示初始状态集合;F⊆Q表示有穷可接受状态集合;C⊆2Q表示无穷可接受条件集合。
特别的,如果|I|=1且δ为Q×Σ→Q,则称 A是确定的完全有穷自动机(Deterministic Complete Finite Automata,DCFA),否则为非确定的完全有穷自动机(Nondescripteterministic Complete Finite Au⁃tomata,NCFA)。
模型检测工具的性质描述是使用ITL公式,而在把ITL公式转换成自动机之前,需要将描述性质的ITL公式化简成基本ITL公式。此时整个公式就只包含原子命题,将CFA字母表中的字符定义为原子命题或其非的集合就可以构造出对应的自动机。对于化简后的ITL公式的原子命题集合Prop,ITL公式的CFA字母表Σ定义为对于任意的非空集合Φ∈Prop,令为了方便起见,令{Δ}(Δ ∈Σs)表示 Σ 所有以 Δ 为子集的字符的集合,即{a |a∈Σ,Δ⊆a} ,特别的true表示集合 Σ 。相应的,用迁移{q1,Δ,q2}(Δ ∈Σs)表示从状态q1到q2存在多个迁移且全部迁移的标记集合为{Δ}。对于迁移{q1,{t r ue},q2}表示q1到q2存在的迁移标记包含了Σ中所有字符。逻辑公式到CFA的构造算法如算法1所示。
算法 1 function cfa(p)
/*前置条件:P为经过预处理过的ITL公式*/
/*后置条件:cfa(P)为公式 P构造的CFA A(P ) =(Σ ,Q,δ,I,F,C ) */
begin function
case
P为原子命题 p:

end case
returnA(P);
end funcation
3.3 系统建模
要使用模型检测工具对一个系统进行检测必须首先对该系统进行建模。状态是描述一个系统的核心概念。状态表示了系统在执行中的某个确定时刻的一些信息,一个状态可以用程序的每个变元的一种赋值来表示,例如一个使用程序变量作为自由变元的一阶公式可以表达一组满足该公式的程序状态集合,其中每个状态都是程序各变量的一种赋值。
利用转换系统建模通常是很方便的。转换系统可以描述系统的行为,在转换系统中,系统可以处于某一个状态。一个转换表示系统的一个操作,在每一个状态上,系统可以执行一系列转换中的一个而到达其他状态。
自动机本身就是一种状态转换系统,在建模时,系统的状态和状态之间转换的条件是比较直观的,转换条件直接用逻辑公式给出,清晰地表达出了系统状态之间的关联。所以我们直接用自动机进行系统建模。为了建模方便我们定义了一种自动机数据格式用来表达自动机,这样可以使用户方便的建模,也方便转换为自动机。自动机数据格式的定义如下。
Model::= {propSet,constSet,varSet,stavarSet,sta⁃tusSet,initStatus,transitions,acceptables,infaccp}
ransistions::= {edge}
edge ::=(s1,cond,s2)
自动机数据格式中propSet是建模时所需的原子命题的集合;constSet是常量集合;varSet是动态变量集合;stavarSet是静态变量集合;statusSet是系统的自动机模型的状态集合;initStatus是自动机模型的初始状态集合,它是statusSet的子集;transi⁃tions是自动机的迁移的集合,每个迁移又是边edge;edge定义中s1和s2是属于statusSet的状态,cond是迁移上的条件;acceptables是自动机可接受条件的集合;infaccp是系统中可以一直循环下去的路径的集合,即自动机无穷可接受条件的集合。
4 系统实现
4.1 系统层次架构
整个系统分为三层,基础服务层、核心功能层、交互界面层。如图3所示。用户交互层主要是用户建模和输入性质公式的接口并呈现模型检测的结果,核心功能层负责实现整个模型检测的算法,基础服务层为核心功能层提供一些通用的功能,例如集合的运算、图的相关算法等。

图3 系统架构
4.2 用户交互界面
用户交互界面如图4所示,图中第一部分是用户输入性质公式的区域,第二部分是用户输入系统模型的区域,第三部分是系统呈现模型检测结果的区域,第四部分是验证开始的按钮。
4.3 核心功能实现
系统的核心功能主要包括两大部分,分别是将性质公式和系统模型转换成自动机再进行运算。在转换过程中用到的主要功能有词法分析、语法解析树构造、自动机的构造以及运算,而自动机的运算包括迁移条件之间的运算和字母之间的运算,还包括子集构造法和预处理这些重点功能。

图4 界面
4.4 基础服务层
基础服务层主要为核心功能层服务。由于系统使用的主要技术是自动机,在系统中自动机是以类似于图的形式保存的,所以有大量关于图的运算功能比如图的遍历等,我们将图的这些算法放在基础层增加了代码的重用性。
系统中的逻辑公式或迁移条件是以集合形式保存的,自动机的运算本质上是边上迁移条件的运算,所以集合的运算功能放在基础服务层。
5 结语
本文通过结合自动机技术实现了有穷论域下区间时序逻辑的判定算法,解决了一阶逻辑判定时变量与函数的处理问题,给出了从区间时序逻辑公式到完全有穷自动机的构造算法,并提出了基于自动机的模型检测工具的建模方法。最后给出了有穷论域下区间时序逻辑模型检测工具的实现方法。
