基于遗传算法的团餐食谱生成算法∗

贺德富 谢 龙

（1.湖北第二师范学院计算机学院 武汉 430205）（2.陆军青藏兵站部 西宁 810000）

1 引言

食谱生成主要有计算法、食物交换份法［1］和计算机生成法［2］。利用计算机生成食谱，具有方便、快捷、准确、高效的特点，已经广泛地应用于糖尿病、“三高”、中小学生等特殊人群食谱生成［3］。苏喜生教授等研究的“模板转换法”［4］可应用于团餐食谱，其基本思路是：1）确定食物范围。根据食物消费习惯，分析得出符合膳食结构需要的各类食物用量的合理范围。2）制定食谱模式。结合团餐要求的伙食费标准与办伙条件确定食谱模式排，即膳食模式中的主食安排、全日主要菜肴数量及质量，特殊品种（主要指牛奶、水果及饮料等）的安排。3）替换算法规则。利用人工智能原理确定规则库，包括当地的供应条件、经实时计算的菜肴价格、加工方法等。4）模板置换。先利用专家知识制订“标准食谱”，根据替换算法规则对同类食物进行替换，得出“派生食谱”。但该算法也存在一定的局限性，主要表现在两个方面：一是标准食谱模板需要大量的专家知识，制订起来需要花费大量的时间和精力；二是替换规则，约束条件少了，生成的食谱可操作性不强，约束条件多了，计算机生成的时间较长，用户可接受性不好。

鉴于此，笔记研究采用遗传算法生成团餐食谱。遗传算法是由Holland提出的，该算法本质上是依照适者生存原则，通过模仿生物进化过程，搜索最优解决方案［5］。遗传算法在使用中具体有编码、初始种群生成、适应度值评估检测、选择、交叉、

∗ 收稿日期：2018年1月6日，修回日期：2018年2月24日

基金项目：后勤信息化重点科研项目（编号：BS215R09025）资助。

作者简介：贺德富，男，博士，教授，硕士生导师，研究方向：计算机与软件工程。谢龙，男，硕士，研究方向：军需信息化。变异和中止等求解步骤［6］。

2 食谱模型构建

食谱是由若干主副食菜肴组成的，每个菜肴又由若干食材组成，通过市场调查的物价信息可以得到可供应的食材数目M，依据可提供的食材，能够获得可加工的菜肴数目为N，用ai标识第i道菜肴，其中i∈［1，N］。根据《食物营养成分表》［7］可以得到每种食材含有的42种营养成分。设每单位的第j种食材含有第r种营养成分的数量为cjr，第j种食材的单价为pj。

将种类繁多的各式菜肴划分为N类，分别是基本主食、花样主食、糕点、蛋品、乳品、大荤、半荤、小荤、全素、小菜、汤、饮料、水果、粥［8］，即N=14。另外每道菜肴包含重量、价格、能量、营养素等属性。则使用一个46维的列向量来表述第i道菜的各个属性。可以表述为

其中：ai1：用以表示第i道菜所属的菜肴类别属性；ai2：用以表示第i道菜的重量属性，单位为克（g）；ai3：用以表示第i道菜的价格属性，单位为元；ai4：用以表示第i道菜的能量属性，单位为千焦；ai5，ai6，ai7，…，ai46：分别表示第i道菜中42类营养素的含量。

其中：i∈［1，N］，j∈［1，m］，m ≤ 6，即一道菜肴最多由6种食材烹制而成。

每种食材都含有价格属性，之前已设定使用pj表示第j种食材的价格，以表示第i道菜肴的第j种食材的单价，则第i道菜肴的价格属性 pi可表述为一个m维的列向量：。

依据式（1）的设定，以ai2表示第i道菜肴的重量，从而有

ai3表示第i道菜肴的价格，从而有

同理，第i道菜肴中含有的能量值和营养素含量为

生成符合需要的团餐食谱重点关注食物定量、伙食费、能量和营养素供给量四个方面，分别以表示。在软件系统中，该值由专家给出默认值，并可由用户根据具体情况自主设定，实现系统适用于不同人群。

食物定量标准中对主食、植物油、副食、燃料等都进行了规定［9］。设对食物定量标准规定的品种数为K，则有：)。依据伙食费和劳动强度的不同，将选取不同的值。对于42种营养素，组成一个向量：，式中，表示每日摄入第r种营养素的理想值。

另外每道菜肴中所含有的各类食物品种的数量是不一致的，如同菜肴“红烧肉”其中就包含了肉类、蔬菜类等。设第i道菜肴第k类食物的重量为，则有：

实际中，食谱的制定应确保该值在理想值的一个可行的范围内。另外，伙食的重复次数过多会造成就餐人员饮食出现乏味，因此应确保一道菜肴在周食谱中出现的次数小于3次，每日该菜肴最多出现一次。设定I为日食谱中菜肴的品种数，xi为日食谱中第i道菜肴在食谱中被选用的情况，则有：

设食谱中某类别的菜肴实际出现的次数为t，则实际出现的次数t可以表示为一个向量：t=(t1，t2，…，t14)。

据以上设定可以得出，每日食谱的食物总重量为

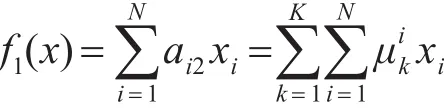
总开支为

总能量值为

各营养素的总量为

令

式中p的一般取值范围为［1，∞），当取p=2时，周食谱要素点与理想点的L2（x）即为欧化距离。我们采用p=2。而优选周食谱的数学模型可表示为minL2（x）。

其约束条件为

其中I为一日食谱中的菜肴总数，带有上下横线的值为理想值的范围。

3 遗传算法使用设计

遗传算法是基于生物进化与选择机制的优化算法［10］。基本遗传算法应定义好编码方式C、适应度评价函数F、初始种群P0、种群大小M、选择算子Φ、交叉算子Γ、变异算子Q、遗传运算终止条件T。据此可以定义为一个8元组：

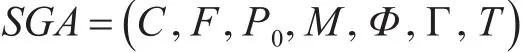
这里对遗传算法的使用进行如下假设：为简化计算，先将主食剔除，即先不考虑军粮定量标准；另假设早、中、晚三餐在菜肴种类上无差别，每餐都包含有4个菜，要求每日菜肴不重样，则每日共计烹制菜肴12种。

使用遗传算法进行食谱生成的一般流程为：首先依据提供的物价供给信息得到伙食单位本周可加工的菜肴种类总数N，这N种可加工的菜肴即为食谱中菜肴的解析库；而后，系统执行遗传算法得到周食谱中一日食谱；再判断该食谱中的菜肴在本周使用次数是否达到2次，如果达到则将该菜肴从解析库中剔除；如果已生成7天的日食谱，则判断本周食谱与上周是否完全一样，如果相同，随机地获取本周食谱中的1/3菜肴，将其从菜肴的解析库中剔除，再重新执行算法，若得到不完全一致的食谱则停止循环，结束使用遗传算法生成食谱，获得算法生成的周食谱，其流程如图1所示。

图1 使用遗传算法生成食谱的流程

3.1 编码方案

遗传算法的使用要求通过编码的方式将要求解的问题转化为遗传中由基因构成的染色体或个体［11］。在对食谱生成问题应用遗传算法解决的过程中使用二进制编码的方式对个体进行编码。由物资供应信息可解得可烹制的菜肴共计N种，并为每个菜肴进行编号，这里使用整数编号，即为1～N。

设12种菜肴为x1，x2，…，x12，xr的数值为在N种可烹制菜肴中对应的编号值，即

因xr为1～N之间的整数，故在使用二进制编码时，由菜肴库中的菜肴数目N确定编码长度，直接将编号转化为二进制数值。若N=100，则可用长度为7的二进制数表示，将xr连接在一起将组成一个个体的基因型，表征一个可行的解。如一个数值为：x=0000111 0001001 0001111 0010010 0010101 0011001 0011110 0100000 0100111 0101000 0101011 0101111的基因型其表示的解为：x=［7，9，15，18，21，25，30，32，39，40，42，47］。

3.2 初始种群的产生

在遗传算法中要对种群执行进化操作，必须要设定搜索的起始点，即选择初始种群。在进行食谱生成中，我们将群体规模设置为20，即群体由20个个体组成，每个个体通过随机方法产生。在生成基因型的过程中，要求不出现相同的xr，即保证菜肴每日只出现一次。

3.3 适应度函数

适应度表征了个体的优劣程度，用以代表个体被选中的概率高低，如果个体的适应度高，其被选中的概率就高，否则其被选中的概率就低［12］。在遗传算法中，适应度函数是区分种群中个体优劣的唯一标准，能够决定是否进行繁殖。在食谱生成问题中，依据之前的设定，每道菜肴包含数量、价格、能量、营养素等属性。通过简化，计算minL2（x）。由于目标函数的值总是非负的，而且目标函数值越小表示越符合，因此可以将求得的值作为个体的适应度，函数F即为适应度函数。

3.4 选择运算

选择算子的作用是确保将种群中适应度高的个体选中并将其基因型遗传到下一代群体中。一般来说，选择运算就是建立起适应度和选择概率的规则或模型，再依据计算的概率来确定个体能否复制到下一代［13］。在进行食谱生成中，适应度越小的个体更应该复制到下一代中，因此应该采用与适应度成反比的概率计算规则来确定各个体复制到下一代群体中的数量。

针对食谱生成问题，在进行选择时将当前种群中所有个体的适应度计算出来，其值可以表示为一个列向量：

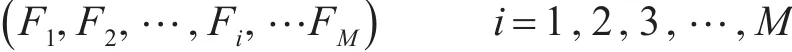
式中的M为这一代群体的个体总量，将群体中所有个体的适应度的反比例值求和，再用个体的适应度值r反比例值除以求和得到的值，则可以获得个体被复制到下一代群体的概率：

遗传算法模拟了自然界的繁殖规律，即越能适应的个体具有更高的可能性繁殖后代，但是并不一定概率越大其具有的后代越多（可能陷入到局部最优解），由此采用轮盘赌选择法（Roulette Wheel Se⁃lection）［14］进行个体的选择。每个个体的概率值表征着轮盘中的一个区域，区域大的表示其概率大，区域小的表示其概率小，全部个体的概率总和为1。使用产生随机数的方法获得一个0～1之间的数值，依据该数值出现在概率区中的次数来判定个体是否被选中。

3.5 交叉运算

在食谱生成问题中个体采用二进制编码，因而在进行交叉运算时，可以采用单交叉点法、双交叉点法、“与/或”交叉法来产生新的个体。在这里我们选择使用单交叉点法进行，其具体的操作方法为：随机的对群体中的个体进行配对，配对的两个基因型为父代基因，再依据基因型的长度随机取得一个数值作为交叉点的位置，在这个位置将父代基因截断，并重新组合得到子代基因型，得到的子代基因型在交叉点前的部分是从一个父代基因中获得，交叉点后的部分从另一个父代基因型中获得。至此可以完成交叉运算。具体的例子如下：

x1和x2为两个父代基因型，其中：

x1=0000111 0001001 0001111 0010010 0010101 0011001 0011110 0100000 0100111 0101000 0101011 0101111

x2=1110001 0010001 1110010 0100010 101001 1001001 1110010 0000010 0111001 0100001 0101101 0111100

假定随机获得的交叉点位置为16，则通过交叉运算获得的子代基因型x1'，x'2为

x1=0000111 0001001 0⋮101111 0010010 0010101 0011001 0011110 0100000 0100111 0101000 0101011 0101111

x2=1110001 0010001 1⋮010010 0100010 101001 1001001 1110010 0000010 0111001 0100001 0101101 0111100

式中“⋮”符号为交叉点的位置，将群体中所有的父代基因进行交叉操作，就得到了新一代的基因型。

3.6 变异运算

在遗传算法中，通过变异运算也可以产生新的子代个体，其运算规则是依照按某一较小的变异概率把父代个体基因型中的一些基因值替换为其他基因值。变异运算的方法也有很多，常用的变异算子为基本位变异算子和逆转变异算子［15］。在食谱生成问题中采用基本位变异算子对父代基因型进行变异运算。其运算规则为：依据基因型的长度随机地确定出3个位置作为变异点，然后将父代基因变异点位置的值进行取反操作，即原来位置是1变异为0，原来位置为0则变异为1。

3.7 算法的终止

当出现适应度值F=0，终止算法；但通常情况下不会出现F=0的情况，这时候就需要将计算的适应度与前几代中的最小适应度进行比较，如果二者相差不大则终止算法。

4 结语

依据食堂所在地域以及季节的不同，采购的食材会呈现出较大的区别。使用模板置换法进行食谱生成未能将这些因素充分考虑进去，致使生成的食谱针对性不强。本算法通过使用公布的物价及供应信息求解出一个适应食堂自身特点的食谱库，再依据遗传算法对构建的食谱模型进行求解，在新构建的食谱库中求解出最优化的食谱，能够较好地解决原有系统在这方面存在的问题。