否定选择算法中高性能检测器的生成

刘恩海，宋瑞平，樊世燕

（河北工业大学 计算机科学与软件学院，天津300401）

0 引 言

主要的人工免疫算法有否定选择算法、克隆选择算法以及免疫网络模型［1］。否定选择算法是Forrest博士在1994年依据生物体中T细胞成熟过程的机制提出的一种免疫算法。算法首先定义一部分自体集合，然后随机产生部分候选检测器集合，在特定的匹配规则下，如果候选检测器集合和自体匹配，则将这些检测器丢弃，只有那些与所有自体都不匹配的检测器集合才能被留下来，作为检测器用以检测异常。由于候选检测产生的随机性，使得否定选择算法的时间消耗与自体集合呈指数关系，当自体集合很大时，该算法会造成时间和空间的巨大浪费，检测效率不高。否定选择算法的主要技术要点包括［2］：问题空间和检测器的表示形式、匹配规则的选择、检测器的生成机制和检测器存储形式。如何快速有效生成检测器是否定选择算法的关键。自否定选择算法提出以来，大量的研究和改进算法被相继提出来。D’haeseleer提出了线性时间检测器生成算法和贪心检测器生成算法，使检测器产生的时间大小与自体集合呈线性关系，尽管贪心算法使检测器的覆盖空间变大，但是这2种算法都不可避免的会产生冗余和漏洞现象。张衡，吴礼发等提出了一种r可变阴性选择算法，通过调整匹配阈值大幅度降低黑洞数量。何申等提出了一种检测器长度可变的否定选择算法，通过检测器长度的变化来提高检测器的覆盖范围。杨铭魁［3］对该算法进行了改进。Lis－kiewicz M等［4］针对穷举法存在的问题，提出了非穷举法。Elberfeld M等［5］提出了压缩法，将检测器集进行压缩将时间复杂度由指数级降低到多项式级，减少了检测器数量。柴争义，张雄美等［6，7］将检测器的表示形式从字符串空间转到向量空间和矩阵空间。王辉，敖民等［8，9］采用可变模糊匹配阴性选择算法，提出了具有一定连续相似度的模糊匹配。大多数文献探讨匹配阈值的变化，检测器长度的变化和检测器形状的改变来生成检测器。基于随机搜索的策略，所产生的检测器具有非常大的检测漏洞，会造成时间和空间的巨大消耗。杨宁等［10］将小生境策略用于否定选择算法以提高效率。张清华等［11］提出了一种新型的针对二进制串的切割否点选择算法。为了提高检测器检测非自体的效率，蔡涛等［12］提出了一种基于红黑树的快速否定选择算法。刘星宝等［13］提出了一个检测器快速生成策略，该算法充分利用自体信息，根据r值大小将自体集分段，得到自体集合相应段的补集，通过二叉树连接得到检测器集合，该算法能保证所产生的检测器不与自体匹配，加快检测器生成的速度，但是该算法会产生大量的冗余，现有的去除冗余检测器的方法是，当新生成一个检测器时，让该检测器与检测器集合中的检测器进行匹配，如果匹配，即此检测器能由已有检测器集合中的检测器代替，则舍弃此检测器，但是该方法会产生二次冗余问题，因为检测器是顺序产生的，先放入检测器集合中的检测器会与后放入检测器集合中的覆盖范围相交，所以经过一次去除冗余并不能保证检测器集合中的检测器不存在冗余。好的检测集集合应该保证：不与自体空间匹配且用最小的检测器集合几乎能够完全覆盖所有的非自体空间。

本文在层次匹配算法的基础上，提取出所有自体集合的以r为大小的段的补集合，在连接策略上进行改进，尽量达到集合的划分，产生能覆盖最大非己空间的最小检测器集合，降低检测器产生的时间，减小检测器个数，扩大等量检测器的覆盖范围，提高检测效果。

1 基于集合的划分与覆盖的检测器集生成算法

1.1 问题描述

否定选择算法的目的是找到一个检测器集合，在不与自体集合匹配的前提下，尽可能多的匹配非自体。由于计算机中的数据和文件都是由二进制表示的，本文将问题空间U定义在二进制串集合上即m＝2。U＝ ｛0，1｝L代表自体、检测器、抗原都以长度为L的二进制串表示。自体集为Self，非自体集为Nonself，根据定义有Self∩Nonself＝φ，Self∪Nonself＝U。Nx：集合X的大小。如Ns表示Self中字符串个数，NR表示检测器集的大小。匹配规则仍采用r连续位匹配规则，即2个字符串若有连续r个位置相同，则2个字符串匹配。例如：11，10在r≤3时匹配。根据匹配规则，2个随机字符串匹配的概率为

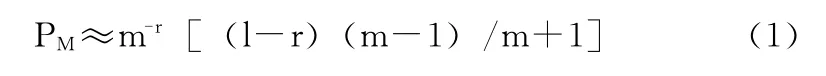
否定选择算法需要首先随机产生一定数量的候选检测器NR0，在固定的匹配概率PM下大小与自体集呈指数关系

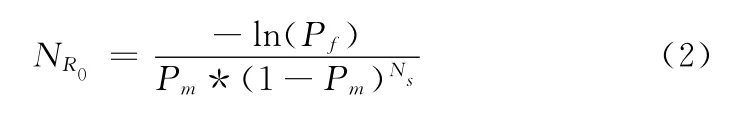
定义检测失败率Pf为一个抗原不能被检测器集合中任一检测器检测到的概率

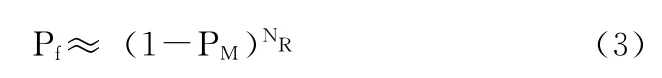
由于无需先验知识，只需利用有限数量的正常样本便能检测出无限的异常数据，使得NS算法被广泛应用，但同时由于候选检测器产生的随机性，每一个候选检测器都要和自体进行匹配，只有与自体集合中的所有自体都不匹配的候选检测器将被保留下来。否定选择算法的时间复杂度取决于2个因素：产生初始检测器集合的时间以及检测器集与自体集中每个数据匹配的时间。空间复杂度取决于自体集大小。在自体集合很大时，该算法会造成时间和空间的巨大浪费，检测效率不高。

1.2 提取补集

由于r连续位匹配规则的特殊性，传统的免疫算法在产生候选检测器的时候，需要和自体进行连续r位匹配，如果匹配则删除或者进行位变异等方法；在检测器抗原的时候，也是利用抗原与检测器进行连续r位匹配，不同的检测器有可能包含同样的检测因子，使得在匹配的时候存在重复提取相同检测器子串造成重复匹配，将耗费大量的时间，使检测效率降低。如果使不同的检测器尽量包含不同的检测因子，这将大大提高检测器的性能。传统的算法没有充分利用自体集的模式信息，本文的检测器生成算法，第一部分采用文献 ［14］中提取自体集每个分段补集的方法，即对长度为L的字符串集合，匹配位长度为r，其每个自体有L－r＋1个分段，依次提取自体集中每段r位字符串，由于包含这些段信息的字符串会与自体匹配，所以根据与2r所产生的全局空间比较得到所有自体段中每段r位字符串的补集，这些补集都不能与自体匹配，因此将作为检测器的组成部分。

例1自体集合为 ｛100000，101101，111001｝。在r＝3时，产生的关于自体集的补集为C1～3＝ ［000，001，010，011，110］；C2～4＝ ［001，010，100，101，111］；C3～5＝［001，010，011，101，111］；C4～6＝ ［010，011，100，110，111］。

1.3 检测器生成算法

上述各个补集的意义为，合格的检测器的1～3位应该为C1～3［］中的字符串；第2～4位应该为C2～4［］中的字符串；第3～5位应该为C3～5［］中的字符串，第4～6位应该为C4～6［］中的字符串，也就是说若C1～3［］中某个字符串的2，3位与C2～4［］中某个字符串的1，2位相同，则可将C2～4［］中字符串的第3位链接到C1～3［］中对应字符串的第4位，因为C1～3［］中串的第4位只有0或1这2种形式，因此可以将串链接的过程表示为二叉树链接的方式，以此类推，直到得到达到固定检测率的检测器集合，但上述做法，势必会造成大量的冗余，因为每个补集段中的字符串只充当一个检测因子的作用，但是其会被多次链接为检测器，这样会造成大量的检测器存在重复检测因子，不但加大了工作量而且降低了检测效率。

1.4 基于集合的划分与覆盖的检测器生成算法

定义1 设A是任意几乎，π是由A的若干子集组成的集合。如果下列3个条件成立：

（1）对于任意c∈π，均有Ai≠Φ；

（2）任意Ai，Aj∈π，i≠j，有Ai∩Aj＝Φ；

则称π是集合A的一种划分。

定义2 设A是集合，如果这些非空子集的并集等于A，则由A的若干非空子集构成的集合称为A的覆盖。集合A的覆盖不必要求2个不同的子集不相交［14］。

算法如下：设字符串长度为L，匹配位长为r，将自体集分段，在全局空间UL对应产生自体集合的补集为C1［］，C2［］…Cs［］。C1［］，C2［］…Cs［］中各个补串的长度为r。

根据集合的覆盖与划分的定义，所产生的检测器集合最理想的情况是链接上补集中所有的串，这样就能产生覆盖所有的非自体空间，同时使补集中的串链接且只链接一次，这样就能保证所产生的检测器集合最小，也就是产生补集的划分，然而在真实的网络检测环境中，所产生的自体集的补集并不能保证都能链接成检测器，有的补集中的串要被链接多次，有的补集中的串一次都不会被链接到。在这种情况下，就要尽可能地产生补集的覆盖，尽可能多的链接上补集中的串，同时使补集中的串重复链接次数最小。

具体实现步骤如下：①从C1［］中的第一个串开始与C2［］中的串进行比较，C1［］中每个串的第2…r位与C2［］中的1…r－1位进行比较，这可能会出现3种情况，C1［］中的串的2…r位与多个C2［］中的串的1…r－1位匹配；C1［］中的串的2…r位与只与一个C2［］中的串的1…r－1位匹配；C1［］中的串的2…r位与C2［］中的串的1…r－1位无匹配。首先链接C1［］中的那些2…r位只与一个C2［］中的串的1…r－1位匹配的串，将C2［］中对应串的第r位添加到C1［］中对应串的后面，这样就能尽可能的向集合的划分靠拢，接着依此规则链接C2［］与C3［］中的串，直到Cs－1［］与Cs［］中的串链接完毕；②对C1［］中每个串的第2…r位与多个C2［］中的1…r－1位串匹配的串，从C2［］中未被链接的串中任选一个进行链接，每次链接都依此规则，形成新的检测器；③经过前面两部骤，补集中会剩下两类串，一类是和本数组内的串有前r－1位匹配，为了保证最大的非自体空间覆盖率，对这类串进行回溯，与前面的补集段中的串进行链接，再向后递归，链接成检测器；还有一类串是不管回溯和递归都不能链接成检测串，对这些串就进行放弃。

依据此算法，对例1中的补集链接成检测器恰巧能构成补集的一个划分。如图1所示。

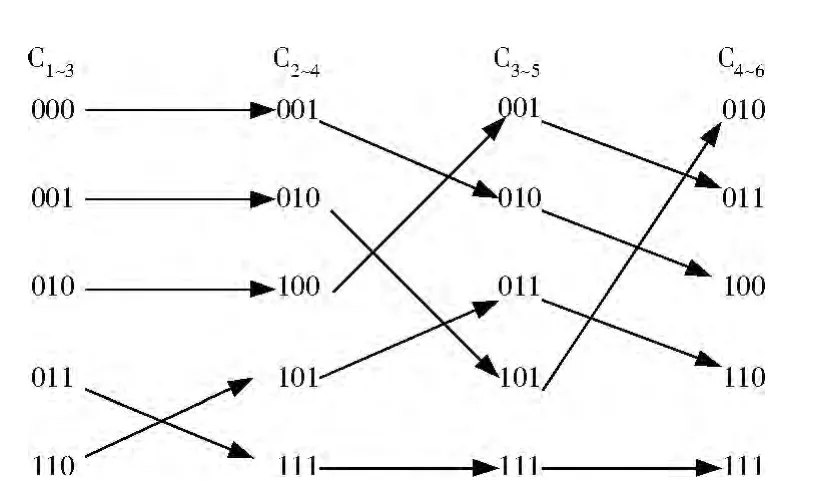
图1 检测器链接过程

产生的检测器集合为｛000100；001010；010011；011111；110110｝。这个检测器集合把自体补集中的所有检测因子都包含在此检测器集中，因此这个检测器集合能覆盖所有的非自体空间，同时由于每个补集中的串链接且只连接了一次，因此这个检测器集合所包含的检测器个数是最少的，比经过去除冗余之后产生的检测器还要少。

复杂性分析：本算法的时间复杂度为产生自体集合相应段的补集的时间和链接成检测器的时间，对于Ns个自体集合依据r连续位匹配，每个自体产生L－r＋1个分段，因此算法第一步的时间复杂度为Ns＊ （L－r＋1）＊r，链接成检测器这一步骤为取到每个补集段中的串按照划分与覆盖的原则进行链接，其时间复杂度为Ns＊ （L－r＋1）＊ （r－1），所以总的时间复杂度为 Ns＊ （L－r＋1）＊（2r－1）。空间复杂度为链接成的检测器集合的大小为：2r－Ns。

2 实验分析

为了验证本文提出的算法的性能和检测效果，本文在Windows7平台下进行了仿真实验。实验环境为：CPU为intel双核酷睿2P7450，内存2G，运行环境为Matlab7.10。为了与已有检测器生成算法进行比较以及简便起见，在这部分的试验中，暂时不考虑检测器的生命周期问题。实验分为两组，第一组测试在同样的检测失败率条件Pf下，去除冗余后的线性时间检测器生成算法，检测器快速生成算法［14］，本文算法，产生的检测器个数比较以及所耗费的时间比较。第二组实验验证在相同数量的检测器个数下，3种算法能成功检测非法集合的概率。实验参数设置及实验过程如下：①L＝8，生成256个8位的二进制串，依次随机选取8，16，32，64，128个二进制字符串作为自体，其余的二进制串作为抗原，位串间采用的匹配位长度r为6。Pf设为0.1，重复随机产生自体个数的步骤50次，统计在不同的自体个数下，3种算法在确定的匹配概率下，需要的平均检测器个数和消耗的平均时间比较；②采用①中产生的检测器，对应相同数量的自体，将剩下的检测器作为抗原，统计在相同数量的检测器个数下，3种算法成功检测非自体的平均值。

由表1可以看出，本文算法相比于前2种算法，在同样的检测失败率下，产生的检测器数量大大减小，同时耗费的时间也明显降低。由表2可知，在同样的检测器数量下，本文算法的检测效率最优，检测效果最好。

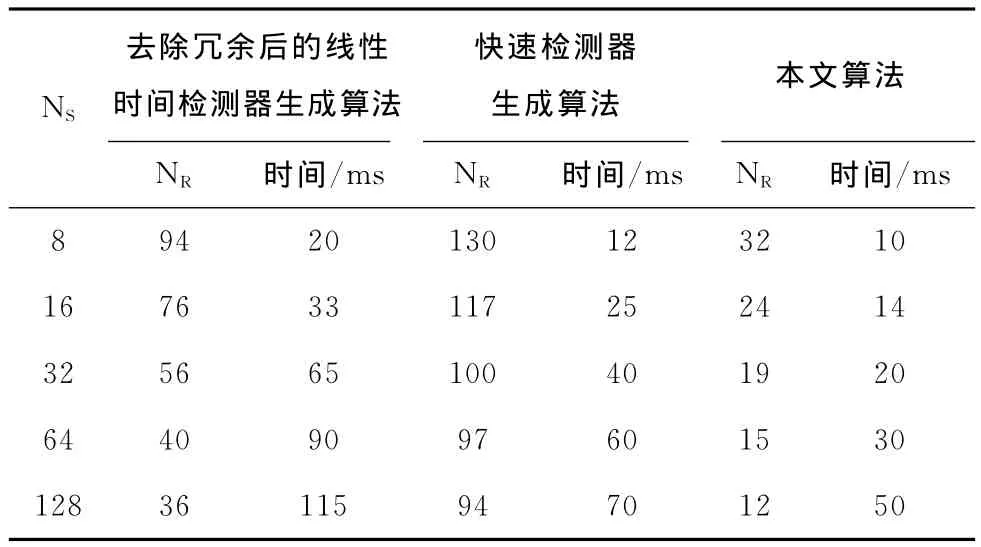
表1 3种算法在固定的检测失败率Pf下所需检测器个数及消耗时间

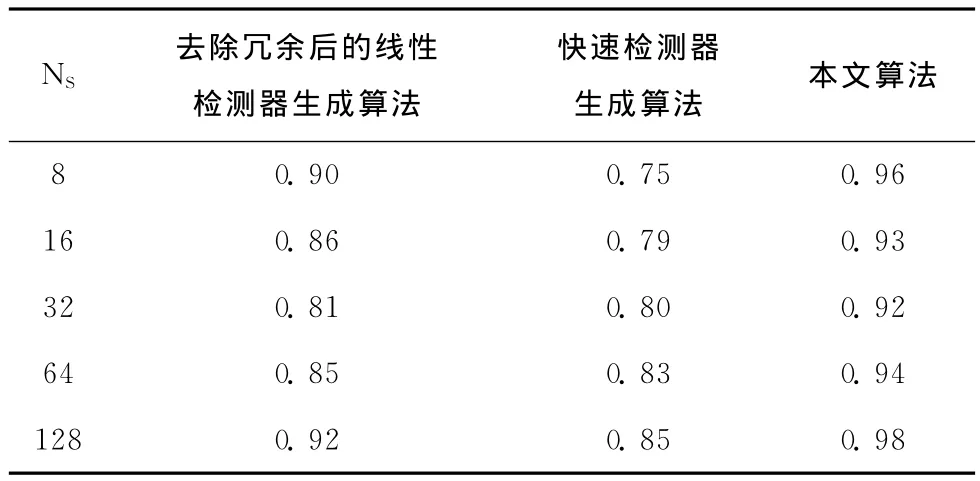
表2 3种算法在相同数量的检测器集合下检测成功率

3 结束语

本文提出的针对集合的划分与覆盖关系的检测器生成算法，能用最小的检测器集合覆盖最大的非自体空间，降低了产生检测器的时间消耗，同时提高了检测器的检测性能。为了进一步提高算法的性能，可以考虑在匹配规则，如何选择参数，消除检测器漏洞等方面进行研究，降低误报与漏报率，提高算法的实时性和有效性。

［1］Dasguptaa D，Yue S，Nino F.Recent advances in artifical immune systems： Models and applications ［J］.Applied Soft Computing，2011，11：1574－1587.

［2］JIN Zhangzan，LIAO Minghong，XIAO Gang.Survey of negative selection algorithms ［J］.Journal on Communications，2013，34 （1）：159－170 （in Chinese）.［金章赞，廖明宏，肖刚.否定选择算法综述 ［J］.通信学报，2013，34 （1）：159－170.］

［3］YANG Mingkui.Improved variable－length detector generation algorithm ［J］.Computer Engineering，2010，36 （15）：174－175（in Chinese）.［杨铭魁.改进的变长检测器产生算法［J］.计算机工程，2010，36 （15）：174－175.］

［4］Lisjuewicz M，Textor J.Negative selection algorithms without generating detectors［C］／／Porland，Oregon，USA：GECCO ACM，2010：1047－1054.

［5］Elderfeld M，Textor J.Efficient algorithms forstring＿based negative selection ［G］.LNCS 5666：Proc of ICARIS.Springer，2009：109－121.

［6］CHAI Zhengyi，WU Huixin，WU Yong.Optimization algorithm for immune real－value detector generation ［J］.Journal of Jilin University （Engineering and Technology Edition），2012，42 （5）：1251－1256 （in Chinese）.［柴争义，吴慧欣，吴勇.用于异常检测的免疫实值检测器优化生成算法 ［J］.吉林大学学报，2012，42 （5）：1251－1256.］

［7］ZHANG Xiongmei，YI Zhaoxiang，SONG Jianshe，et al.Re－search on negative selection algorithm based on matrix representation ［J］.Journal of Electronics ＆ Information Technology，2010，32 （11）：2701－2706 （in Chinese）.［张雄美，易昭湘，宋建社，等.基于矩阵形式的否定选择算法研究 ［J］.电子与信息学报，2010，32 （11）：2701－2706.］

［8］WANG Hui，YU Lijun，WANG Kejun，et al.An adjustable fuzzy matching negative selection algorithm ［J］.CAAIT Transactions on Intelligent Systems，2011，6 （2）：178－184 （in Chinese）.［王辉，于立君，王科俊，等.一种可变模糊匹配阴性选择算法 ［J］.智能系统学报，2011，6 （2）：178－184.］

［9］AO Min.Research on detector generating algorithm based on negative selection ［D］.Chongqing：College of Computer Science of Chongqing University，2010：29－43 （in Chinese）.［敖民.基于阴性选择的检测器生成算法研究 ［D］.重庆：重庆大学计算机学院，2010：29－43.］

［10］YANG Ning， WANG Qian.Negative selection algorithm based on niche strategy ［J］.Computer Science，2011，38（10A）：181－184 （in Chinese）.［杨宁，王茜.一种基于小生境策略的阴性选择算法 ［J］.计算机科学，2011，38（10A）：181－184.］

［11］ZHANG Qinghua，ZHAO Hongxia，ZHU Yuejun，et al.Generate detector on novel negative selection algorithm ［J］.Electronic Design Engineering，2010，18 （11）：8－11 （in Chinese）.［张清华，赵红霞，朱月君，等.一种新型的否定选择算法生成检测器的研究 ［J］.电子设计工程，2010，18 （11）：8－11.］

［12］CAI Tao，JU Shiguang，NIU Dejiao.Efficient negative selec－tion algorithm and its analysis［J］.Journal of Chinese Computer Systems，2009，30 （6）：1171－1174 （in Chinese）.［蔡涛，鞠时光，牛德娇.快速否点选择算法的研究与分析［J］.小型微型计算机系统，2009，30 （6）：1171－1174.］

［13］LIU Xingbao，CAI Zixing.Fast detector generative strategy for negative selection algorithm ［J］.Journal of Chinese Com－puter Systems，2009，7 （7）：1263－1267 （in Chinese）.［刘星宝，蔡自兴.负选择算法中的检测器快速生成策略 ［J］.小型微型计算机系统，2009，7 （7）1263－1267.］

［14］DENG Huiwen.Discrete mathematics［M］.Beijing：Tsinghua University Press，2010：29－32 （in Chinese）.［邓辉文.离散数学 ［M］.北京：清华大学出版社，2010：29－32.］