一种基于GPU的实验变差函数计算优化算法

朱家成 田善君

（1.江汉大学数学与计算机科学学院计算中心 武汉 430056）（2.中国地质大学（武汉）计算机学院地质信息技术研究所 武汉 430074）（3.山东交通学院交通土建工程学院 济南 250000）

1 引言

变差函数是Motheron在1965年提出的一种区域变化估计方法。数学解释为区域化变量增量平方的数学期望，变差函数的实际意义是，它反映了区域化变量在某个方向上某一距离范围内的变化程度，是地质统计学克里格方法的基础操作工具，能够有效地描述区域化变量在空间上的结构性与随机性［1～3］，并可以在其他领域作为分析区域化变量随机性和结构性特征的有效工具。

在地质统计学领域变差函数的实际应用中，我们通常都将求解变差函数过程分解为实验变差函数计算和理论变差函数拟合，目前主流的研究都是针对理论变差函数的拟合，因为理论拟合的参数好坏能决定一个变差函数应用于地质统计学的精确度。所以早期的地质统计学研究领域主要是对变差函数理论拟合进行优化，很少有涉及对实验变差函数的计算过程进行优化。而得到一个稳健的实验变差函数是进行理论拟合的基础，且在当前实际应用中，局限变差函数应用的一个主要问题就是数据量增大时，急剧下降的实验变差函数的计算速度。真正在地质统计学的应用中，得到一个能满足实际生产应用的实验变差函数结果，需要不断进行不同方向上多个参数下的变差函数计算调试，需要来回多次进行实验结果的比对，而每次计算的过程都是一次复杂的运算［1］。

在地质统计学储量估算领域，我们会对三维空间内的钻孔采样点建模之后进行变差函数的计算，从而可以更加形象具体且真实的反映某个矿体的品位含量的三维空间的结构性和随机性，进而估算储量。而真实的地矿数据较为庞大，在实际应用过程中，阻碍储量估算的难题已经不再是对理论变差函数拟合的优化来提高估算精确度，而是繁琐的实验变差函数计算严重影响了储量估算的计算时间。一次完整的三维储量估算过程，采用传统的方法，需要多次的实验变差函数调试，每次调试的过程都需要大量的计算，严重影响了整个计算过程，所以地质统计学领域急需一个优化的实验变差函数计算算法来解决这个难题。

2 三维空间实验变差函数

变差函数的基本定义是区域化变量增量平方的数学期望，也就是区域化变量增量的方差［3］。通常为了便于生产计算需要，一般取值半变差函数，本文在计算过程中，也遵循这一规则。总得来说可表述为在相距为h的两个空间点x和x+h的权值Z（x）和Z（x+h）之间的方差，因此可得计算公式如下：

式（1）是在理想状态下，有无穷的样品对参与计算，最后求出一个平均值，其中，Z（x+h），Z（x）表示在x+h与x两个不同位置时，样品点的权值，而上式又称为理论变差函数。而在实际应用中，区域内变量的数量是有限的，且取不同的增量值，会对样品对数影响较大，增量值越大，样品数越少；增量值变小，样品数目会增多。而样品对数越多，算出的结果才更准确，有实际意义，但样品数越多则会造成计算量的增加。而在地质统计的实际应用中，确定的空间位置点x0上只能有Z（x0）的一次观测值，即样品对的个数是有限的，故可以得到式（2）。

在式（2）中，N（h）表示相距为h的样品对的数目，显然可以看出，实验变差函数是一个根据h的变化而变化的一条函数曲线，如图1所示。

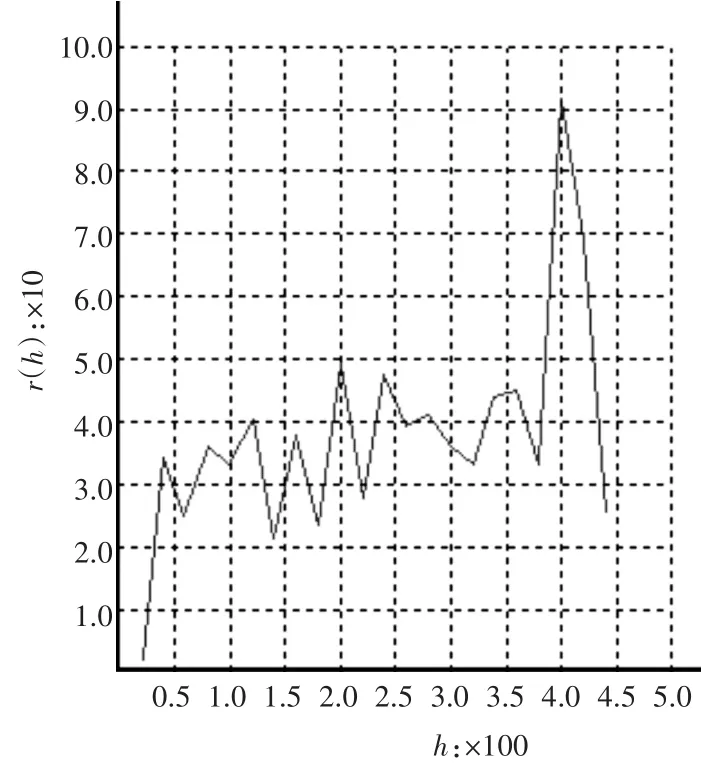
图1 实验变差函数曲线图

2.1 不规则样品对的选取

在真实的环境中，样品数据往往都是不规则分布的，这就需要我们采用一定的处理方法才能获取能够参与运算的有效数据。

2.1.1 非三维空间的不规则数据处理

1）一维数据

当数据处于一维分布，也就是待处理的数据都在一条直线上。如果我们还是按照固定的步长来计算的话，能够满足要求的样品对会非常少，所以我们增加在距离上的约束，也就是两个样品点之间的距离在步长的约束范围之内存在一定的容差，满足容差的样品对都属于合格样品对。

距离容差可以保证在一个确定的方向上增加入选的样品对，但容差也不能设置的太大，不然就会导致很多不符合计算要求的样品对也被规划进来。

2）二维数据

当数据处于二维分布，也就是待处理的数据都在一个平面上。那么所选样品对除了在距离上进行容差设计之外，还要在方向上进行一定的容差设计，也就是在方向上也要增加一定的角度范围活动区间，属于该范围内的样品对都属于符合要求的样品。如图2所示。

图2 角度容差示意图

假设点A分别与点BCD来进行角度判断，有箭头标志的直线为基准方向，那么样品对（AB）、（AC）、（AD）都属于符合基准方向的样品（假定夹角小于等于角度容差）。

2.1.2 三维空间不规则数据的处理

显然，真实的地质统计学过程中，数据都是在三维空间分布，在一维和二维的数据分析基础上，把距离和角度的约束都添加进去，为了便于进行更好的数据结果分析比对与计算，以及算出的结果更有实际意义，可以参照自己一维，二维分布的容差涉及，在三维实际应用中也对每次参与的样品进行角度和距离的容差设计，便于更好地获取能够参与计算的样品对，如图3所示。

图3 三维角度距离容差示意图

2.2 三维稳健实验变差函数结果的调试

为了更好地获得区域化变量在空间的结构性和随机性，以及为下一步的克里格插值做准备，在进行三维空间变差函数分析时，通常会进行三个两两相互垂直的方向作为求得实验变差函数结果的方向。这个三个方向的获取，则是根据式（2）进行不同方向变差函数结果的比对而来。根据以上分析我们可以得到三维稳健实验变差函数结果的计算流程大致如下：

简单来说计算流程主要可分为以下几大步骤：

1）样品数据模型的建立，即区域化变量的位置信息以及品位信息建模，即公式中任意样品点A，B的位置xi与权值Z（xi）；

2）约束范围模型的建立，确定角度约束，距离约束，以及其他条件约束，得到约束范围内的两两样品对库；

图4 三维实验变差函数流程图

3）计算符合约束范围的单个实验变差函数值，得到当前范围的实验变差函数结果；

4）变差函数结果的调试，专家进行当前实验变差函数结果的判定是否能达到后续工作的要求，进行不同的调试与重新计算的选择；

5）稳健实验变差函数结果的生成，进行多次的实验变差函数结果的调试之后，可以先后确定三个方向上的稳健三维空间实验变差函数结果。如图所示黑色和灰色实线表示相互垂直的第一第二方向，虚线表示与前两个方向分别垂直的第三方向。

图5 三个相互垂直方向计算样品图

3 GPU加速的优化算法

由以上步骤可以看出实验变差函数的计算中，每一个Rz的计算是在确定一个固定的参数之后继而实施同种类型的运算，具有模块化和数据弱相关的特点，符合CUDA编程模型的“数据并行处理”机制，故可以采用GPU进行计算性能上的加速。该步骤主要体现在计算流程中的“计算半变差值”模块里。

3.1 计算过程的优化整合

基于GPU架构的CUDA编程模型本质上是一种流式计算，适用于数据并行处理的问题。数据并行是将数据划分成子数据流，在一些相同执行过程的程序模块上对这些子数据流进行处理。这种方式的并行效果并不受问题求解步数的限制，只受制于相同处理模块的数目和系统内部的通信宽带，并行度很高且具有良好的可扩展性，可以构建包含大规模运算模块的空间分析系统。

传统的实验变差函数计算效率低下的原因在于：传统的算法在实现时没有考虑到整个实验变差函数值得计算过程所表现的内在的处理并行性。

通过对式（1）变差值的计算过程，我们可以看出，每次重新约束规则进行一次新的计算，都是进行若干个半变差值的计算，而一个个样品对进行变差值的计算又是相互独立互不影响的过程，即多次不同参数下的同种类型的运算，故可在上述传统三维稳健实验变差函数的计算流程中，将计算半变差值的过程，用CUDA编程模型进行运算过程的加速。

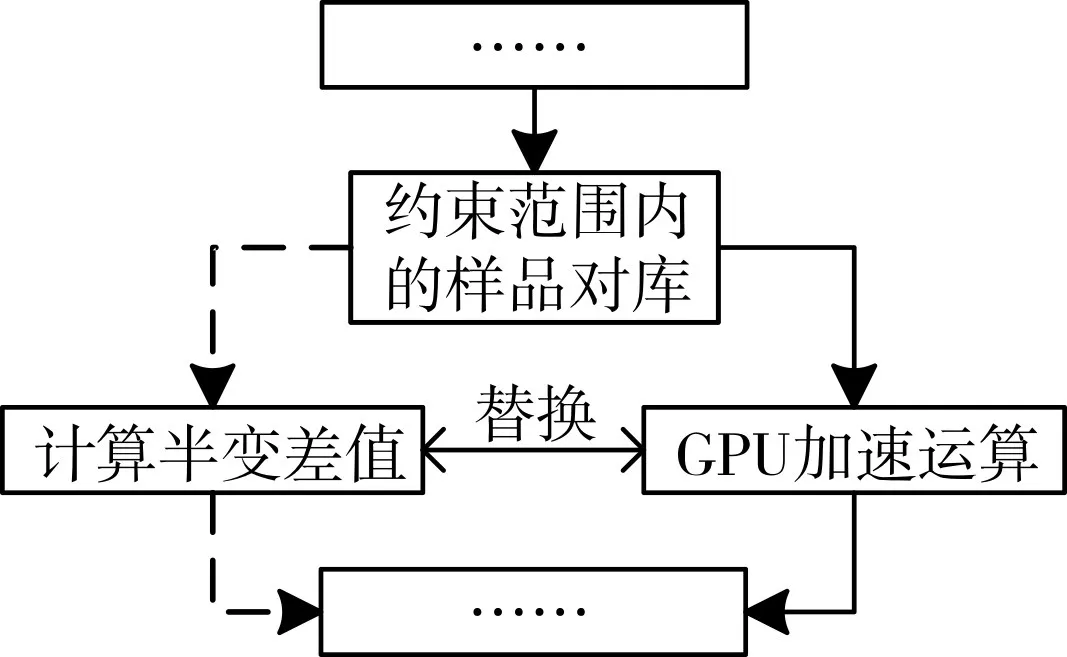
图6 运算过程的替换

3.2 算法实现

3.2.1 建立模型

建立数据模型即创建一个需要进行实验变差函数计算的三维模型，包括几何信息模型与属性信息模型。为了更便于操作以及空间展示，我们将每一个样品都设计成三维空间圆点或者中心线的形式，属性信息以隐藏的方式存储，只有在调用的时候才展示出来。

Input：样品的几何信息，属性信息。

Output：样品数据模型。

1）创建样品对象CPoint（X，Y，Z，Atr）；

//其中X，Y，Z表示样品对象的空间坐标，Atr表示该样品对象的属性权值；

2）依次循环，将几何信息，属性信息读入创建的每一个对象；

3）进行数据模型信息的可视化输出以及结构输出；

//可视化输出表示对象的三维展示，结构输出表示记录当前的数据文本信息。

而建立约束模型，则需要在根据不同的专业领域，根据专家意见设定一个初步方向约束与距离约束，我们在一定范围内，设定方向约束与距离约束的调试范围。

Input：约束规则的参数值，约束的表现形式。

Output：样品的约束模型。

1）创建约束的表现形式CSearchCone，Cline；

//CSearchCone，Cline分别是一个圆锥体和直线段，为方向约束与距离约束的表现形式

2）根据样品数据模型的参数确定约束规则的大致参数范围；

3）将获取的约束规则参数值赋予以上两个约束对象；

4）确定约束变动的规则与范围；

5）约束模型的可视化输出与结构输出；

同样下图展示了约束模型在三维图形显示平台中的展示形式与形态，圆锥体表示方向约束，中间的直线距离约束。

在进行约束规则更改之后，约束方向，或者约束长度都可以进行改变。

3.2.2 并行计算过程，建立样品整体库

并行计算的过程，实际上是计算样品对的半变差值，样品对空间距离以及样品对的法向量。通过CUDA平台，编程实现GPU加速。

1）根据当前硬件条件确定CUDA中的Block的尺寸，再根据数据的规模确定Block的数量；

在本次实验中，每个线程块使用512个左右的线程进行并行计算，而Block的数量可以使用文件数据量与每个线程块线程之比来计算。

2）根据CUDA全局内存的容量和数据的规模，确定数据分块的大小和数目，以便完成多批次计算。具体计算方法如下：

EleNum=MaxPitch/（Z*sizeof（float））

BlkNum=（m*n+EleNum-1）/EleNum

其中MaxPitch是从CUDA函数接口获取的允许函数最大pitch的拷贝尺寸。

3）使用CUDA函数在显存中开辟数据计算空间和并行计算结果空间，将层之间的数据按照分块形式依次从内存传入显存中，并设计核函数进行计算；

4）使用CUDA函数将计算结果从显存转移至内存，保存至文件中。

而整体样品库的建立，则是依据CUDA函数的输出结果，依照样品库Sap=（SapBasic，SapVar，Sap⁃Length，SapAngle）的结构，依次将样品库所需要的信息录入。

3.2.3 输出实验变差函数计算结果

在以上前期工作全部完成之后，接下来就是进行调试输出，即根据当前约束规则，快速得到该约束规则下的实验变差函数计算结果。

1）将约束规则的变化转换成参数大小的改变；

2）将改变后的约束参数与样品整体库中的Sap对象进行约束规则比对，当条件符合，则记录下该对象；

3）把所有符合约束规则的对象进行统计，按照实验变差函数的坐标曲线进行结果输出；

4）判断当前的结果是否符合下一步计算要求，如果符合则完成运算，如果不符合，重复步骤1）。

图7 输出实验变差函数

4 试验结果

4.1 算法比对

上面主要介绍了GPU加速的实验变差函数优化算法，并在理论上与两种不同的计算方法进行了对比。通过分析可以发现，该算法比传统算法在快速得出大规模数据实验预期结果的速度上有着显著的提高。因此我们结合两个算法的特点，进行了算法的优缺点分析：

1）传统算法，实质上是按需所求的进行计算，根据当前约束条件，得到约束条件内的样品对，每确认一个样品对，进行一次计算。该计算方法，没有复杂的调用过程，运算简单清晰，在不需要大量调试，数据量比较小的环境里，该算法计算速度很快，但该算法所需环境在真实工程应用中效率会大大降低；

2）GPU加速算法，在传统算法计算的基础上，考虑了计算半变差值的并行特点，在该计算过程采用GPU加速。这种方法在传统的方法基础上，对计算过程进行了加速，在原始数据空间分布均匀的环境里，不需要进行多次约束就可以快速得出稳定的实验变差函数结果。

根据上面的分析，可以对以上两种算法的优点和缺点进行总结如表1所示。

表1 两种实验变差函数计算算法有缺点比较

4.2 实验比对

本次试验所采用的数据，设有试验模拟数据，真实矿山数据等，包括点状样品数据模型和线状样品数据模型，根据不同的规模划分为5个数量级。

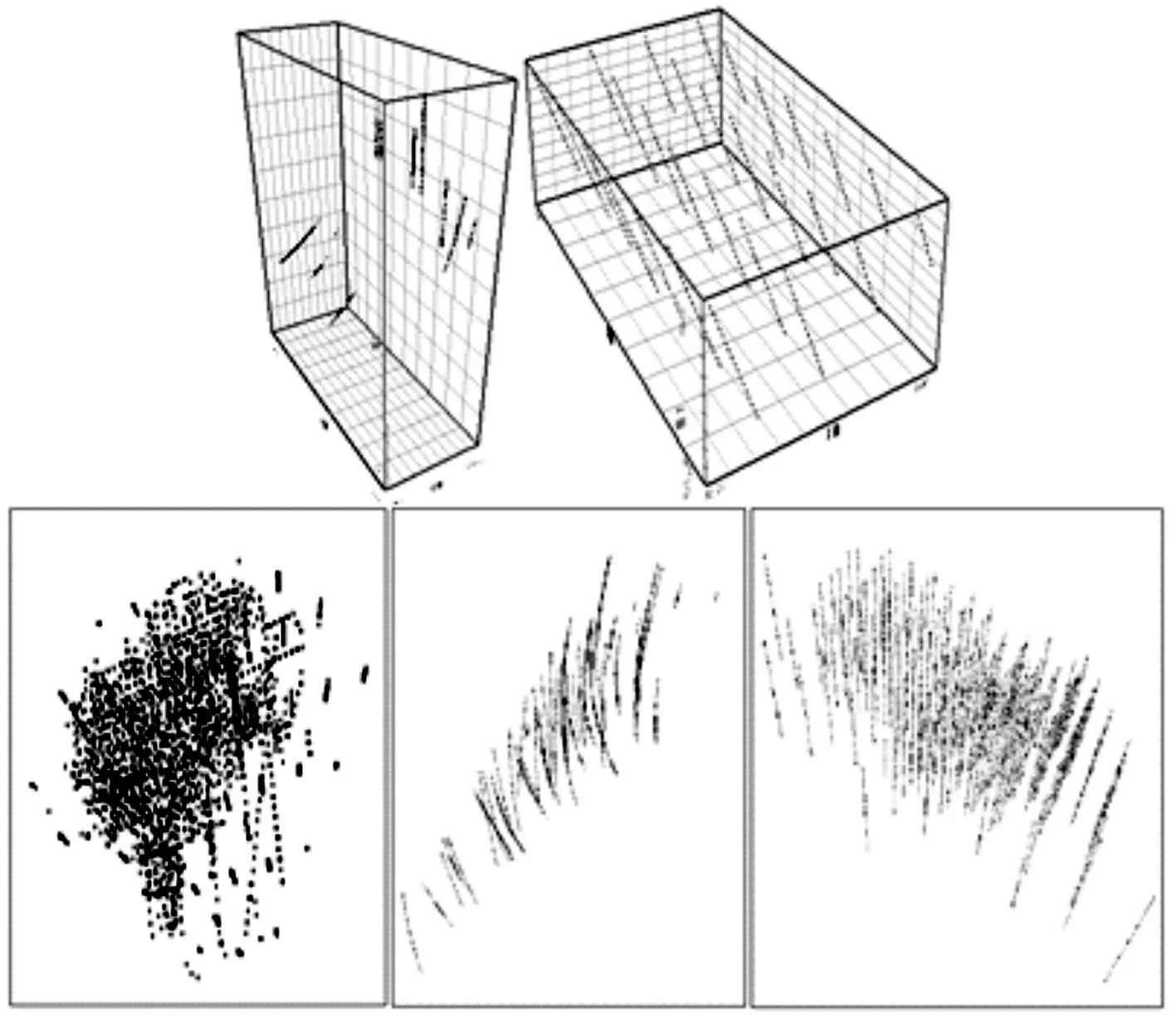
图8 五组数据

将以上五组实验数据分别用本文优化算法比较，因稳健的实验变差函数结果需要专家进行每次计算结果的分析比对，故将实验结果分为两部分：首次计算与调试计算，可得出实验结果如下：

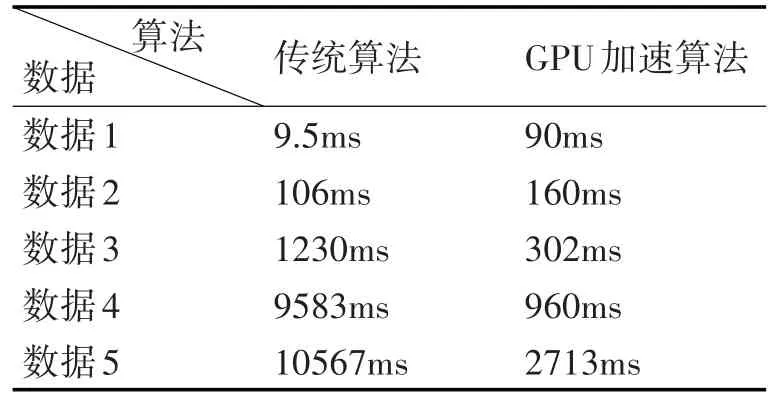
表2 首次计算三种算法结果比对

由表2可以初步得知，在首次计算过程中，GPU加速算法和传统算法，在数据量增加的过程中都有较明显的优势。

由图9也可以看出随着数据量的增加，两种加速算法比传统算法优势越来越明显，且单纯GPU加速算法比整体到局部算法还稍有优势，当然一次完整的实验变差函数的计算过程，绝不可能只是一次计算就能得出正确结果，故需要进行后期的调试计算。

图9 算法首次运行时间对比图（单位：ms）

表3 调试过程一次计算耗费时间比对

则可得相应的对比图如图10所示。

图10 调试一次耗费时间对比图（单位：ms）

一次完整的过程所耗费的总时间为首次计算时间与调试时间的总合。

即TA=TF+（TD1+TD1+TD1+…+TDN），其中TA为耗费的总时间，TF为首次计算时间，TDi为单次调试时间，调试次数N会随着数据的改变而改变，一般情形N≥15。

表4 15次调试三种算法时间对比

从上表3、4可以看出，优化过后的算法，在实验变差函数的计算过程中有着显著的优势，并且，当数据量增大，优势会更加突出。

5 结语

综上所述，本文提出了一个三维空间实验变差函数优化算法，并应用到真实的地质统计学应用软件中去，可以解决真实环境中实验变差函数计算效率低下的问题，且通过多种数据下的实验验证了实验的目的。

当然本次算法也有不足之处，通过对约束分析，我们可以看到，每次进行一次新的约束，都可能存在着与前一次约束相同的样品对重复计算，所以本文的算法虽然通过GPU加速，能够提升计算效率，但仍因为重复的样品对，导致了大量的时间与空间的浪费，所以如何能够优化这个过程，是解决这个问题的关键。一次性把所有样品对的实验变差值结果通过GPU加速算法计算出来，再进行实验变差函数计算的约束分析之后，判定哪些计算结果是符合约束条件的样品对是一大难题，因此以后的工作室设计一个便于后期进行约束筛选的样品对库来实现实验变差函数的进一步优化。