基于分解数据库的FP-growth算法关联规则研究∗

刘 艺 张海涛 刘奇燕 石 硕

（1.中国海洋大学信息科学与工程学院 青岛 266100）（2.云南中烟工业有限责任公司技术中心 昆明 650024）

1 引言

关联规则挖掘是从大量事务数据库中发现事物之间相关关系的一个重要课题，主要采用Apriori算法和FP-growth算法两种经典的方法进行挖掘［1］。Apriori算法是在由Agrawal等提出的一种经典的关联规则挖掘算法，该算法采用逐层搜索的迭代方法，进行多次扫描数据库，从而得到频繁项集。然而在数据量较大时，由于必须多次扫描数据库以及产生大量的候选集，使得算法运行效率较低。随后J.Han等提出一种FP-growth算法［2］，将数据库压缩到一棵频繁模式树（FP-tree），对于频繁模式树进行挖掘从而得到频繁项集。此种算法只需扫描两次数据库且不会造成大量候选集的出现，较Apriori算法在运算效率以及空间效率上都有一个量级的提升。然而，FP-growth算法仍存在以下的一些问题：构造的FP-tree占用空间较大，重复递归产生大量的子树，对于空间要求很高［3］。

目前关联规则分析在医疗领域上应用较为广泛，主要有以下几个方面的研究：根据病人的各项数据，对患者进行分类在此基础上提取患有某类疾病患者相关特征，从而辅助医生对患者病情的诊断［4］；通过医疗处方分析找出某类疾病与医疗处方间关系，以辅助医生开具处方［5］等，但关联规则对疾病并发症的挖掘研究相对较少且缺少与患者体征相结合的研究［6］。

针对上述问题，本文基于糖尿病患者并发症及其体征的相关统计数据，提出一种改进FP-growth算法，算法主要结合散列表、分解数据库的思想以及在提取规则时增加约束条件，在提高效率的同时，使得产生的规则与本文所研究内容的相关性更大。该方法能有效地对糖尿病并发症进行关联规则的挖掘，获得糖尿病与高血压，高脂血症，冠心病之间并发的概率，在此基础上将糖尿病患者结合体重指数进行分类，挖掘出体重指数对于糖尿病并发症发病影响的定量关系，从而为糖尿病三种主要并发症的前期预防提供参考。

2 方法

2.1 FP-growth算法

FP-growth算法主要采用频繁模式增长的策略进行挖掘，将所有数据压缩至一棵FP-tree，从中递归的发现一些短模式，然后与后缀连接。算法主要分为构造FP-tree和挖掘FP-tree两步，如下表1过程所示。

表1 FP-growth算法过程

关联规则的挖掘是由FP-growth算法挖掘频繁项集后，从中获得满足最小置信度与最小支持度的强关联规则［7］。

设A、B分别为事务中的两个项集，关联规则是形如A⇒B的蕴含式。关联规则A⇒B在事务数据库中成立，具有支持度support(A⇒B)，A和B同时出现在事务中的概率即support(A⇒B)=P(A∪B)。关联规则A⇒B在事务数据库D中的置信度confidence(A⇒B)，表示事务在包含A的条件下同时包含B的概率即confidence(A⇒B)=P(B|A)。

2.2 改进FP-growth方法

针对FP-growth算法存在的占用空间大等问题以及医疗数据的特点，本文提出一种基于数据库分解［8］以及规则约束的方法。主要从以下方面进行改进：

1）基于散列表的改进

散列表（Hash table）这种数据结构可以直接根据键（Key）来访问内存存储位置。该结构可以通过计算基于关键值k的散列函数，将需要查找的数据映射到表中的位置，加快了查找速度［9］。

FP-growth算法挖掘过程中，第二遍扫描事务数据库时，需要将事务中的项按照支持度递减的顺序排列，此时需建立头表用于查询支持度计数以便进行排序，而头表通常使用的是顺序存储结构。在查询某项的支持度计数时需要从第一项开始遍历直到遍历到相关项为之，效率较低。

基于散列表的思想，不使用顺序存储而是使用散列表作为头表的存储结构，并构造相应的散列函数，在查询某项的支持度计数时，直接通过散列函数映射到对应数据位置。较遍历头表的方式，基于散列表数据结构存储频繁项列表，提高查找频繁项集支持度技术的效率。

2）基于分解数据库思想的改进

将事务进行划分并存储于链表中，对于划分后的事务分别进行关联规则的挖掘，无需建立所有事务的FP-tree。

在FP-growth算法中所构造的FP-tree是将整个数据库中的数据压缩至一棵FP-tree中，基于集成了全部数据库信息的FP-tree进行关联规则的挖掘，生成的FP-tree需求的内存较大，且影响算法效率。

基于分级数据库的改进方法，采用分治的策略，使用链表存储遍历整个数据库后的结果，将事务中的各项根据支持度递减进行排序，将排序后的事务根据其首项分类，生成各个子数据库，对于各子数据库使用FP-growth算法进行数据挖掘，提高效率的同时节省了空间。

3）基于强关联规则左右约束的改进

由挖掘算法获得频繁项集后，首先找出频繁项集的所有非空子集，每两个子集间生成一个关联规则，计算所有关联规则组合的置信度，从中选择大于最小置信度阈值的规则即为强关联规则［10］。

例如由频繁项集I=｛i1，i3，i5｝，由I所产生的非空子集有｛i1，i3｝，｛i1，i5｝，｛i3，i5｝，｛i1｝，｛i3｝，｛i5｝。由非空子集之间进行组合产生该频繁项集的所有关联规则，计算每项规则的置信度，输出大于阈值的规则。

在此过程中，产生了多条关联规则并需要对其进行计算，对于本研究中的事务而言，我们期望得到糖尿病并发症相关的关联规则，则只需要糖尿病相关项出现在关联规则的左部，而其他并发症的相关项只需要出现在关联规则的右部。基于这一需求，对于强关联规则的获取进行改进，增加关联规则左右部的约束，减少产生无趣的关联规则条数，同时可减少在生成强关联规则过程中的计算量，运算效率得到了提升［11］。

2.3 方法步骤

本文主要结合散列表、数据库分解、关联规则左右部约束对FP-growth算法进行了改进，具体步骤如下：

1）第一次扫描数据库D，获取频繁1-项集以及事务中每个项的支持度计数，按照支持度计数递减排列保存于L中，将L存储于散列表中构造相应函数 F（k）。

2）分解数据库

（1）第二次扫描数据库D，使用步骤1）中所构造的散列函数F（k）查询每个事务中项的支持度计数，按照支持度计数递增进行排列，得到数据库记为D1。

（2）扫描数据库D1，依据L中项的顺序，将事务按照首项分类存储到链表Ki中，含有相同首项的事务存储到同一链表项下，形成如下图1所示结构。从中提取所有首项为项 Ii（i=1，2，…，n）的事务，将这些事务存储于链表Ki中。

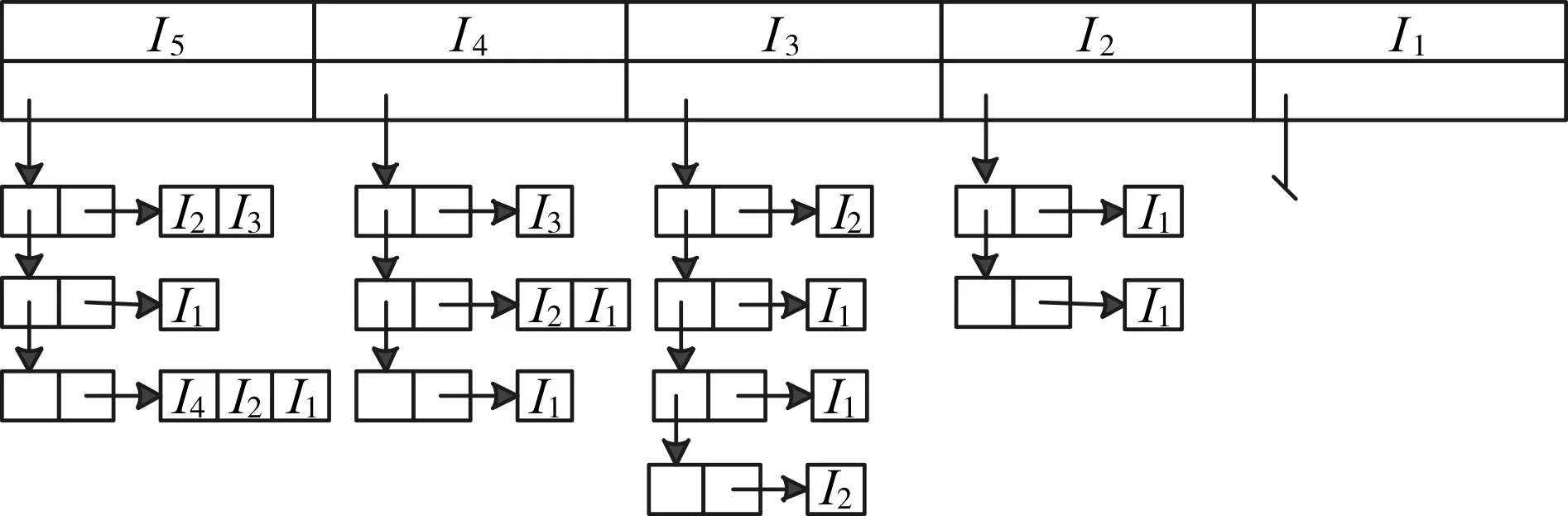
图1 链表结构图

（3）从链表 Ki导出首项为 Ii（i=1，2，…，n-1，n）的事务，将事务中的项按照支持度计数递减排列生成数据库D2，对于D2使用FP-growth算法步骤进行挖掘，输入数据库D2输出频繁项集。

（4）将D2中事务从数据链表中删除，同时删除D2事务中的首项，根据其后继项将删除首项的事务重新添加到数据链表中。

（5）重复步骤（3）、（4）直至数据链表为空。合并每次挖掘的结果，即为数据库D所有的频繁项集。

3）获取关联规则

从获得的频繁关联项中提取关联规则，在由频繁关联项生成非空集合时，对所生成关联规则的左右部进行约束。设 F=｛F1，F2，F3｝为事务中项的约束标记，对于事务中的项设置三种约束，分别如下：F1表示，项只能出现在关联规则的左部；F2表示，项只能出现在关联规则的右部；F3表示，项既可以出现在项的左部又可以出现在项的右部。将事务中的项根据需要进行相应的约束标记后计算置信度与支持度，从而获得关联规则。

3 实验验证

3.1 实验数据

为了验证本文算法的有效性，同时挖掘糖尿病并发症与体重这一体征间的关联规则，从某医疗机构采集了患者的相关个人信息以及部分体征信息。患者年龄集中在50岁～70岁之间，数据中记录了患者患有的疾病及相关并发症（包括：糖尿病、高血压、高脂血症、冠心病）以及查体所获得体征信息具体数值（包括：体重指数、收缩压、舒张压、空腹血糖、糖化血红蛋白、总胆固醇、甘油三酯），数据结构如图2所示。从中获取本实验所需的数据，包括患者所患有的疾病以及并发症、体重指数，经过预处理后进行实验。

图2 体征信息

3.2 预处理

由于实验数据存在不规范等问题，在数据挖掘前，针对上述数据特点从以下几个方面进行相关预处理工作：

1）数据选择：从所有数据中随机选择5517条数据作为实验数据。

2）数据清洗：去除噪声，噪声指的是存在着错误或异常的数据，同时去除一些无关数据。

3）数据变换：将数据集变量转换成整数型的数据，分别使用数字1～5代表糖尿病，高血压，高脂血症，冠心病，肥胖这五种疾病，将每个患者的患病情况作为一个事务。本研究选用BMI≥28作为肥胖的标准，而根据通用标准体重指数在24～27.9之间则视为超重，在数据预处理中发现大部分患者属于超重的状态，所以选用一个较高的标准。

本文主要研究糖尿病及其并发症的关联规则，以及肥胖对于并发症的影响，因此选用两组数据分别进行实验，经过处理的数据如图3（a）（b）所示。图3（a）包含糖尿病及其三种主要并发症，用于研究糖尿病与其并发症的关联规则。图3（b）包括糖尿病并发症及肥胖数据，用于研究肥胖对于糖尿病并发症发病概率的影响。

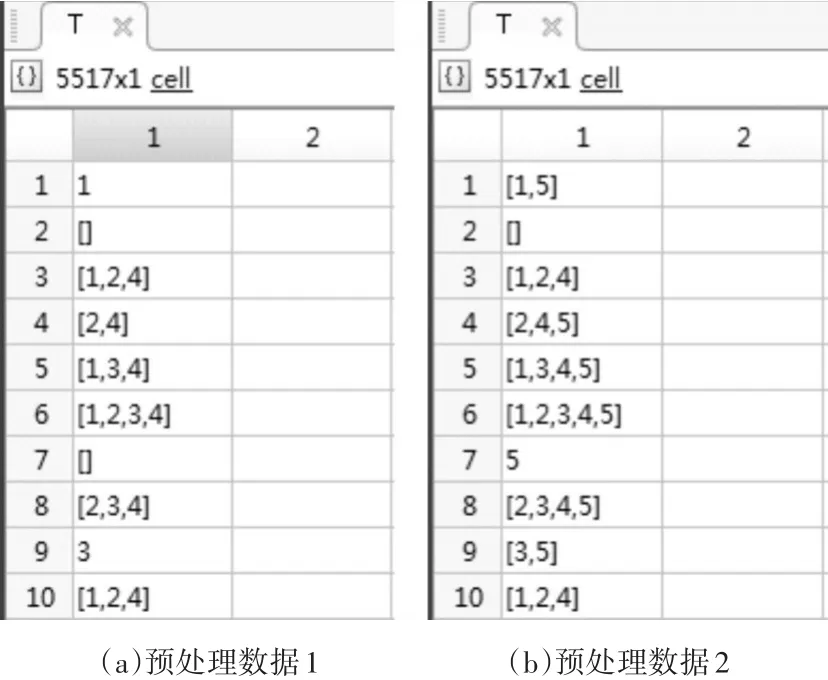
图3

3.3 仿真分析

3.3.1 关联规则分析

表1、表2为使用本文提出的改进的FP-growth算法进行挖掘的结果。由于都定义了最小支持度阈值和最小置信度阈值Minimum Suppport Threshold=0.05，Minimum ConfidenceThreshold=0.1，在关联规则满足条件时，才会作为一条关联规则。此外，本研究还引入了作用度（Lift）作为另外一个标准来提高关联规则的准确度。作用度是可信度与期望可信度的比值，其计算公式为Lift(A⇒B)=P(B/A)P(B)，只有在作用度大于1时，此条规则才被视为有意义的规则，即是规则中两个事物呈正相关的关系。

表2、表3所表示的含义如下：对于关联规则A⇒B，Suppport（支持度）表示同时患有多种疾病A和B的概率，Confidence（置信度）表示在患有A种疾病的情况下，同时患有B种疾病的概率。

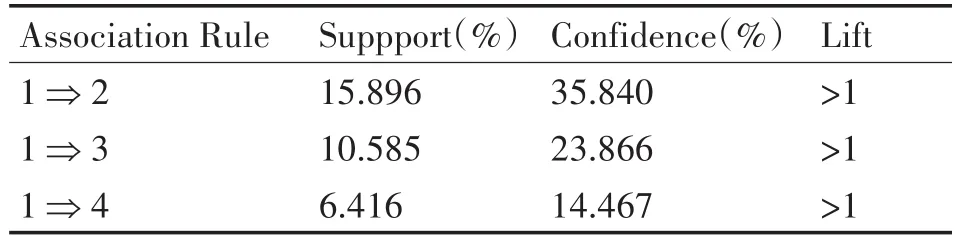
表2 糖尿病与高血压、高脂血症、冠心病关联规则

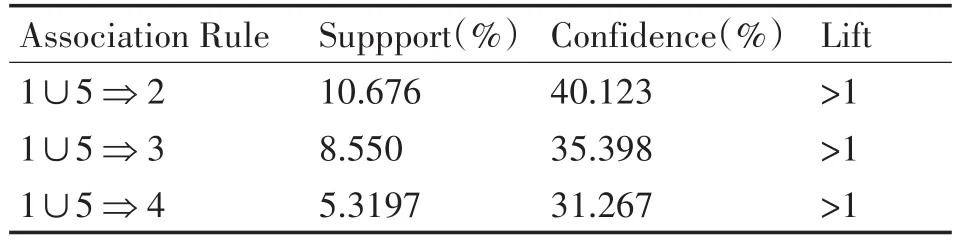
表3 糖尿病并发肥胖与高血压、高脂血症、冠心病关联规则

通过表2糖尿病与高血压、高脂血症、冠心病关联规则可以看出，同时患有糖尿病及高血压的概率最大Suppport(1⇒2)=15.896，糖尿病并发高血压的概率也是最大Confidence(1⇒2)=35.840，其次是高脂血症，再次是冠心病。

通过表3糖尿病并发肥胖与高血压、高脂血症、冠心病关联规则表示患有肥胖症的糖尿病患者与其三种并发症的患病概率，可以看出，患有高血压的可能性最大，其次是高脂血症，再次是冠心病。此结果与糖尿病并发症结果一致，在此基础上，研究进一步发现，体重指数超重的糖尿病患者并发高血压、高脂血症、冠心病的概率均较体重指数正常的糖尿病患者高。

从实验结果来看，肥胖是糖尿病患者并发高血压、高脂血症、冠心病的一个重要危险因素，应对此引起重视。

3.3.2 算法效率对比

为了进一步验证本文算法的有效性，与经典Apriori算法和FP-growth算法的效率进行了对比分析，使用同样的数据，分别设置最小支持度阈值为2%、4%、6%、8%、10%比较三种算法的运行时间，结果如图4所示。

可以看出，如果事务数量相等，最小支持度越大，算法的时间效率越高。三种算法对比发现，在每一个设置的最小支持度情况下，本文所提出的改进算法运行时间最短，FP-growth算法运行时间次之，而Apriori算法的运行时间最长，而且最小支持度越小，算法的运行时间差值越大。由此可见，本文所采用的改进的FP-growth算法能够更加高效地进行关联规则的挖掘。

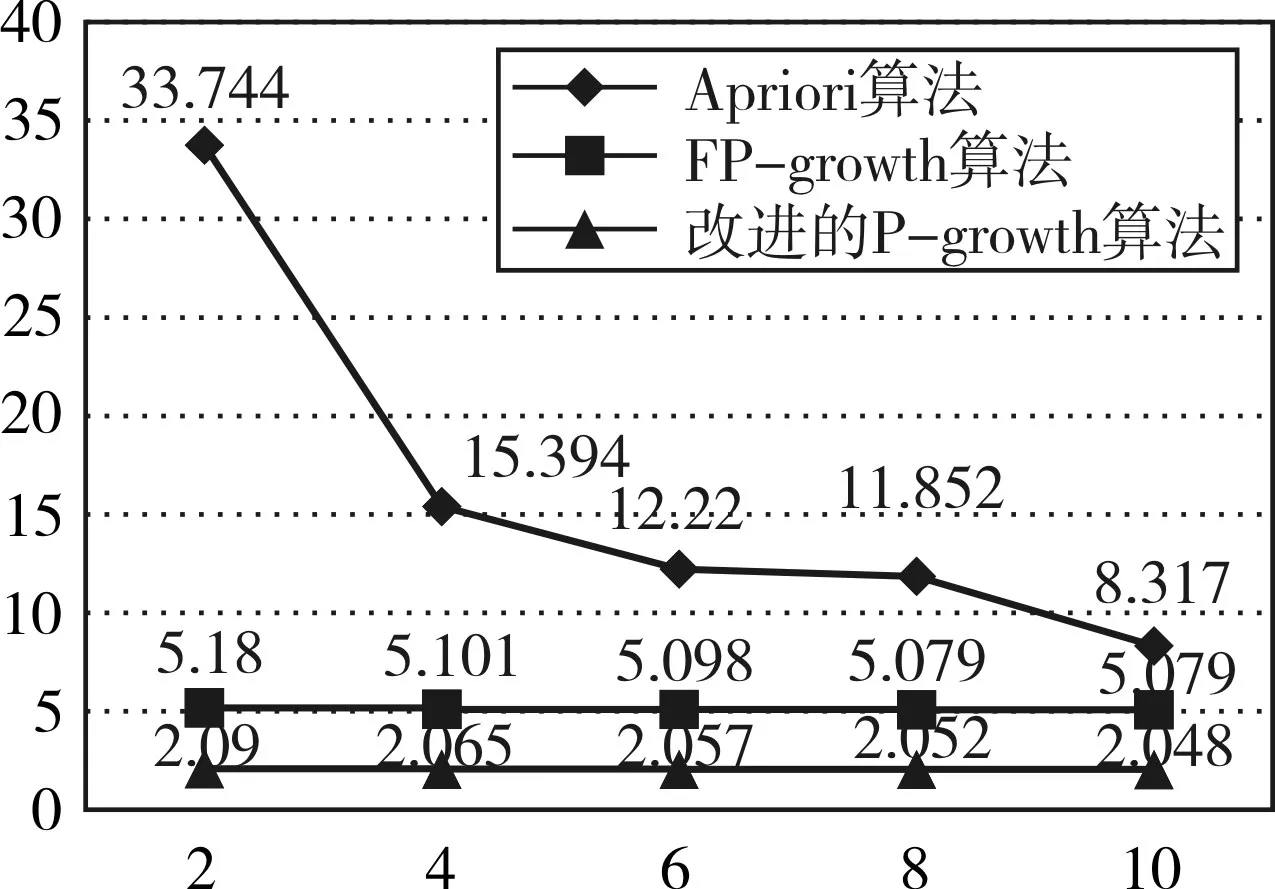
图4 算法运行效率对比图

3.3.3 关联规则数量对比

在提高效率的基础上，本文对关联规则的输出进行了条件约束，使用如下约束：对于5（肥胖），只能出现在关联规则的左部，使用F1进行约束标记；对于2（高血压），3（高脂血症），4（冠心病），只能出现在关联规则的右部，使用F2进行约束标记；对于1（糖尿病），既可以出现在关联规则的左部，又可以出现在关联规则的右部，使用F3进行标记。经过改进后的算法所得出的关联规则数量较原算法有所减少，从而减少了计算量提高算法效率，同时减少不感兴趣的规则的出现，提高了所得关联规则的有效性。

图5为本文改进的FP-growth算法与FP-growth算法使用相同数据进行实验所得关联规则数量的对比。可以看出，使用位置约束后的改进算法较原经典算法所生成的关联规则数量明显减少，可有效减少计算量同时避免产生研究所不感兴趣的关联规则。

图5 关联规则数量对比图

4 结语

本文在经典FP-growth算法的基础上，提出一种更为高效的改进FP-growth算法，该算法对关联规则的产生进行了约束，增强了所产生规则的有效性，提高了运行效率。在对于糖尿病及主要并发症（高血压、高脂血症、冠心病）关联规则挖掘的基础上，进一步研究了患有肥胖症的糖尿病患者与其主要并发症之间的发病率关系，为糖尿病并发症的预防诊断等提供了一定的参考性，同时本研究发现肥胖对于糖尿病并发症发病率有显著影响，这对于医务人员以及患者都有一定的参考价值。