一种填充空心玻璃微珠的粘弹性聚合物声学特性研究

向 平，丁晓冬

（中国船舶工业系统工程研究院，北京 100094）

0 引 言

在水声功能材料应用中，内含散射粒子（如重金属，空腔等）的粘弹性复合材料一直受到各国科研人员的广泛关注[2-8]。其理论分析主要有（半）解析方法和数值方法。在（半）解析方法中，常用的方法为传递矩阵法[1]，其可方便处理多层介质。如果多层介质中某层或多层是内含散射粒子的复合材料，其核心是求得该复合材料的等效频变参数，然后利用这些等效参数，采用传递矩阵法分析多层介质的声学性能。在复合材料等效参数的求法中，针对球形散射体的理论模型最具代表性。常用方法有单体共振理论[2，4]、自恰理论[5-6]。单体共振理论未考虑散射体间声波的多重散射，即从一个散射体发出的散射波不再被另一个散射体散射，这种方法通常用于求解散射体填充分数较低的复合材料等效参数。自恰理论则根据微观局部应变张量，以匀化技术（homogenization technique）考虑散射体间声波的多重散射效应，所以这种方法常用于求解低频条件下复合材料的等效参数。另一类方法是数值方法，通常采用有限元法建模[7-8]，其缺点是计算本文三组元复合介质时，网格规模较大，计算效率较低，且不易于揭示声学机理。

近年来，声子晶体的研究方兴未艾[9-16]。声子晶体内部通常含有周期排列的散射体，如圆（棱）柱以及球（立方）体等。声子晶体的研究为非均匀复合材料声学性能的研究提供了重要的理论基础。I-vansson[11]利用声子晶体发展的多重散射法，分析了含有周期球状空腔的粘弹性橡胶的消声性能。结果表明，考虑多重散射效应后，覆盖层消声频率与基于单体共振理论所获得的消声频率间存在明显差异。最近，三组元复合材料的研究引起了人们的关注[4，6，12-13，16]。相对于二组元复合材料来说，三组元复合材料的模型复杂度增加，但其可实现二组元复合材料所欠缺的功能。其中，以包覆硅橡胶的铅球形成的局域共振结构为散射单元[12]，可实现低频段共振吸声[13]；以空心玻璃微球（微珠）为散射单元，可增强复合材料承受外部水压力的能力[4，6]。

在低频段，由于波长远大于散射体尺寸或相邻散射体间距，可利用散射体周期排列来近似实际样品中散射体位置随机分布，Ruffa[17]曾利用这一思路计算水中气泡的低频声学性能。受这一思路启发，本文采用声子晶体领域发展出的多重散射理论[14-16]，假设散射体位置周期排列，严格根据应力应变连续条件，通过Bloch定理简化内含空心玻璃微珠的聚合物复合材料声衰减特性的分析，并与Baird等人[4]的实验测试结果相比较，说明了近似模型的有效性，然后分析了单个空心玻璃微珠的Mie散射特性，讨论了空心玻璃微珠填充分数对聚合物复合材料声衰减性能的影响。

1 模型与多重散射理论

1.1 周期近似分析模型

在填充空心微珠的聚合物复合材料内部，散射体大小及位置分布通常具有一定随机性，这给聚合物复合材料声学性能的分析带来了一定的困难。为简化分析，将聚合物复合材料内部的空心玻璃微珠人为周期分布，形成散射体三维周期分布，用于聚合物复合材料声学性能的近似分析。根据固体物理晶格理论，在笛卡儿坐标系下，散射体三维周期分布可形成分层结构。其中，层内沿XY平面为二维结构，如图1（a）所示。 散射体位置可通过两个基矢确定，分别为a1=a0（1，0，0），a2=a0（0，1，0 ）。 相邻层间的相互位置定义矢量a3=（a3x，a3y，a3z），一列平面纵波沿Z轴入射，如图1（b）所示。a3取值不同，形成不同的点阵形式。 如a3=a0（0，0，1 ）形成简单立方结构，a3=a0（1/2，1/2，1/2 ）形成体心立方结构，a3=a0（1/2，1/2，）形成面心立方结构等。为简化分析，我们假设散射体排列沿XY平面无限延伸。图1（c）给出空心玻璃微珠结构，其中阴影部分为玻璃，内部为空气。包覆层内外半径分别为r和R。

图1 空心玻璃微珠周期近似排列分析模型Fig.1 Periodic microsphere distribution model

1.2 多重散射法

假设均匀介质内弹性波位移随时间具有谐波分量e-iwt，则位移满足如下与时间分量无关的二阶偏微分方程：

其中：ρ为介质密度，λ，μ分别为拉梅常数，u为位移矢量。在球坐标系下，位移矢量可分解为：一个纵波（L）模式，其代表介质位移沿径向的振动，以及两个剪切波（M和N）模式，分别代表介质沿球面切向两个正交方向的振动，即

在多重散射方法中，散射波场与入射波场间的关系是通过单体的Mie散射矩阵[13-16]获得。对于图1（a）中坐标原点的散射体来说，其散射波可用球面波展开，

其中：σ=1，2，3 分别对应 L，M，N 模式，Hlmσ（）r与第一类球Hankel函数[15-16]有关。该散射波取决于总入射波，包括外部入射波和来自其它散射体的散射波之和。外部入射波可用球面波展开为

其中：Jlmσ（）r与第一类球Bessel函数有关。来自其它散射体的散射波为

其中：rj表示以散射体j中心为原点的空间任意点的坐标向量。Rj表示散射体j的坐标向量。根据Bloch定理，空间周期性可保证

其中：k//为正方形点阵（如图1（a）所示）不可约布里渊区倒格波矢。上述系数B=blmσ｛｝通过散射矩阵完全取决于系数获得单层散射体的透射和反射矩阵，则须把外部入射波（（4）式）以及总散射波，即球面波展开分别转化成平面波展开形式。对于入射波，平面波展开如下：

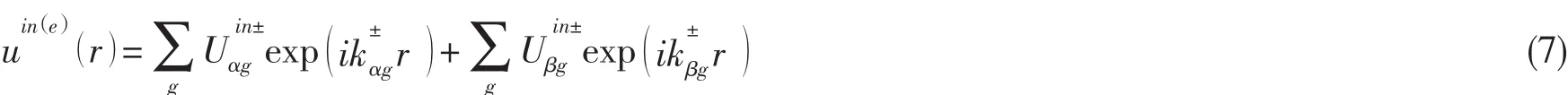
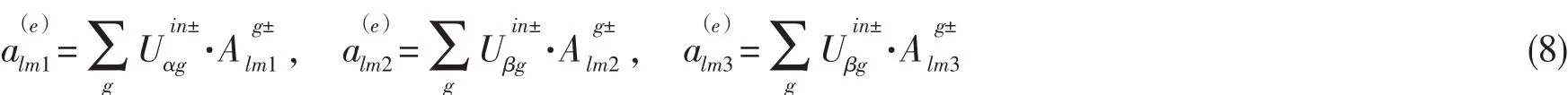
对于散射波有

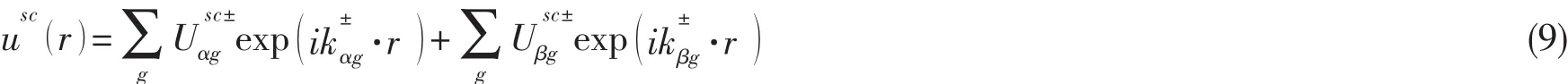
相应地，球面波展开系数与平面波展开系数之间的关系为：

一旦求出单层散射体的透射和反射矩阵（系数），通过迭代运算，就可获得与（11）式相类似的多层结构入射波和透射波位移场关系。当入射波仅从左表面沿Z轴正向入射时，（11）式中右边界沿Z轴负向传播的波U-（R）为零。通过引入纵波能量可获得能量透射系数t。文中定义声衰减，即隔声量为-10lg（t）。

2 结果与讨论

为了与Baird的实验测试结果相比较，空心玻璃微珠的几何及材料参数均取自参考文献[4]。其中，空心玻璃微珠外径R=5×10-5m，玻璃壳填充率取Fg=1-（r/R ）3=2.5×10-2， 可计算出内径 r=4.958×10-5m。材料参数见表1，材料阻尼通过复弹性模量引入。其中，基体聚合物的动态剪切模量实部与损耗因子均随频率变化，满足如下关系：

其中：f为频率，单位取Hz。Ai和Bi值与参考文献[4]相同。基体复剪切模量为μ=μR1-i（）η 。

表1 文中所用材料声学参数Tab.1 Acoustic parameters of adopted materials

图2（a）-（d）分别给出空心玻璃微珠填充分数分别为5%，9%，13%和17%时粘弹性聚合物复合材料的隔声量。计算中复合材料板厚均为1 cm，且沉浸在水中。其中，虚线和实线分别表示微珠简单立方和面心立方排列近似模型分析结果，而十字点表示Baird等实验测试结果。从图2（a）可看出，即使在空心玻璃微珠填充分数较小（如5%）时，与相同厚度不填充玻璃微珠聚合物板的隔声量（如图2中点划线所示）相比较，含散射粒子的复合材料虽然质量密度减小，但隔声量有很大提高，此时，空心玻璃微珠主要通过调节复合材料等效阻抗和声耗散来增加复合材料声衰减。从图2还可看出，隔声量随频率的增大而逐步提高。如在100 kHz附近，隔声量提高约5 dB。在周期近似分析模型中，由于面心立方结构比立方结构配位数（coordination number）高，即在给定散射体周围具有更多的相邻散射体，这标志着面心立方结构中散射体的分布相对更为均匀，所以其性质更接近于实验中散射体位置随机分布（在散射体与基体充分混合的条件下，可近似看作相邻散射体不接触）的复合材料声学性能。这一点可从图2中看出，当空心玻璃微珠以简单立方排列时，计算隔声量远大于实验测试结果，误差较大。而微珠以面心立方结构排列时，计算隔声量与实验结果在各填充分数下（特别当填充分数小于10%时）基本吻合。随着填充分数的增大，高频分析结果略高于实验测试结果，但最大误差小于3 dB，如图2（d）所示。与Baird等人的理论分析相比较可看出，本文与Baird等人分析得出的隔声量在高频均略高于实验测试结果。如在填充分数为17%时，Baird等人高频分析的最大误差约为4 dB（见参考文献[4]中图5）。

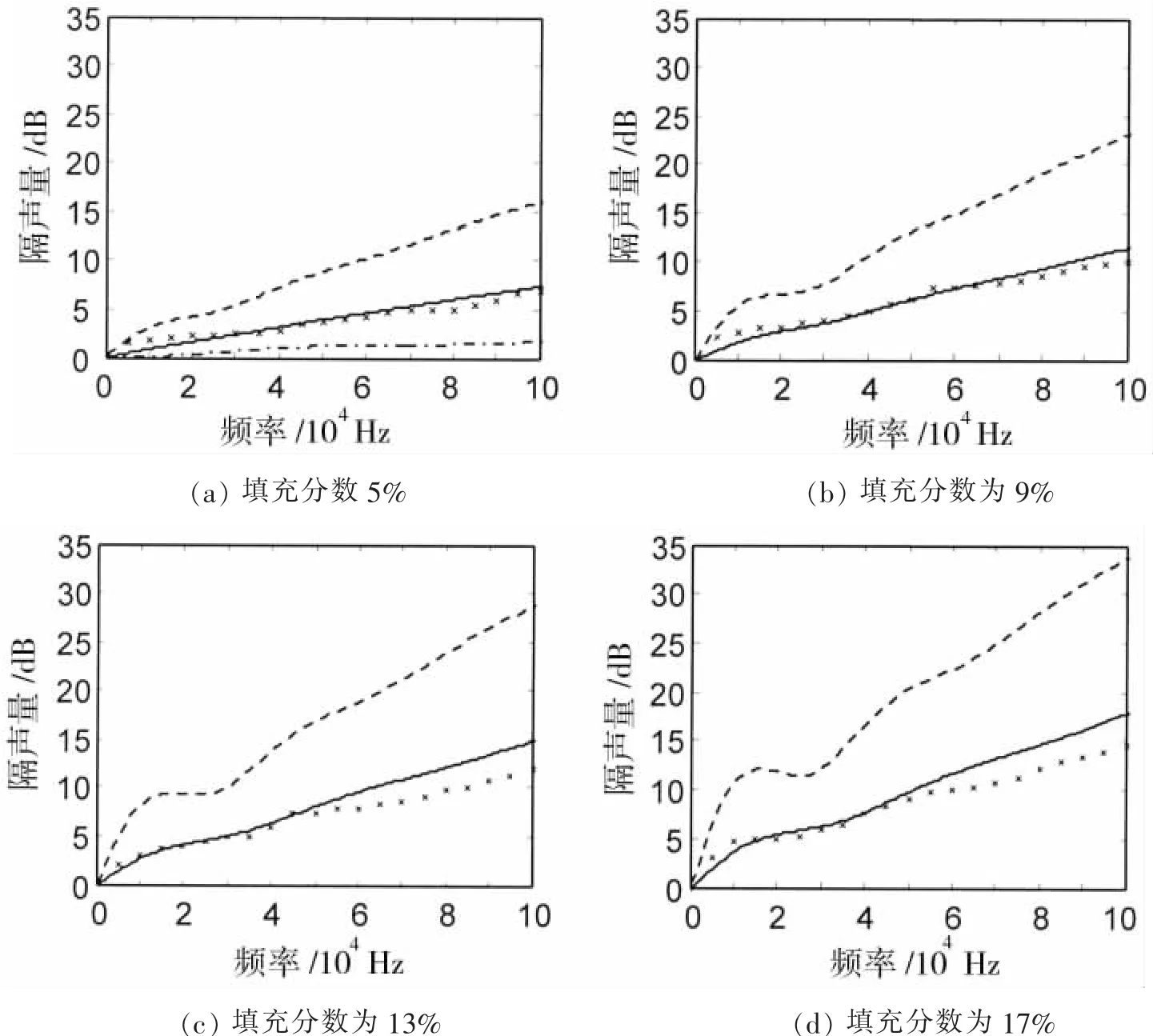
图2 含空心玻璃微珠的粘弹性聚合物复合材料板的隔声性能Fig.2 Transmission loss of a polymer slab containing hollow glass microspheres with different filling fraction(a)5%;(b)9%;(b)13%;(d)17%

由于复合材料的声学性能在很大程度上依赖于单个空心玻璃微珠的Mie散射特性，为了较好地理解复合材料的声学特性，下面深入分析了复合材料中单个空心玻璃微珠的Mie散射特性。分析发现，仅零阶Mie散射矩阵（T0）中元素LL幅值存在明显非零值，这标志着微珠径向振动比较明显。图3给出微珠散射矩阵T0中元素LL幅值绝对值随频率的变化。其中，峰值标志着微粒的径向共振，而阴影部分则表示文中分析频段。从图中可看出，文中分析频率远低于微珠共振频率，属于低频准静态区，这正是等效媒质模型有效的依据[4-6]。在该频段，入射波长远大于空心玻璃微珠直径和相邻微珠间距，在此条件下，用玻璃微珠周期排列，可有效分析微珠无序排列的复合材料隔声性能，同时避免了引入统计理论分析散射体随机分布所带来的误差。与Baird[4]以及Haberman等人[6]的理论分析结果相比较，可看出本文的分析与他们的分析结果非常接近。

从图2中可看出，复合材料隔声量随空心玻璃微珠填充分数的增加而增大。如果进一步增加空心玻璃微珠的填充分数，则隔声量进一步增大，如图4所示（计算中微珠以面心立方排列近似）。

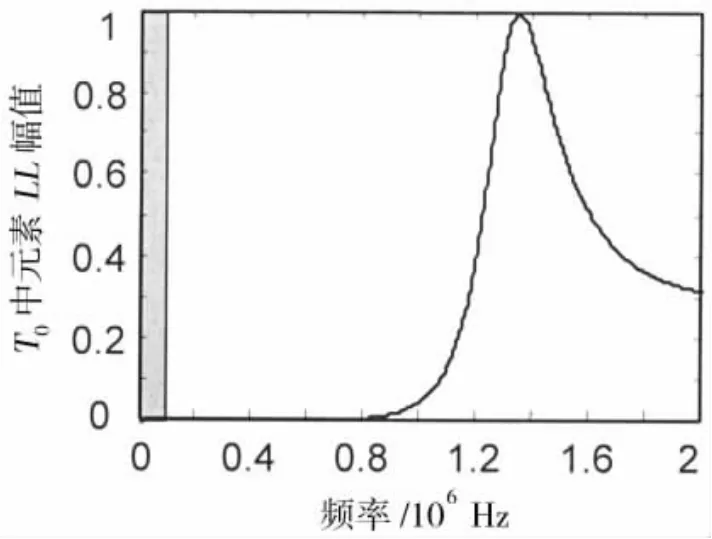
图3 单个空心玻璃微珠在聚合物基体中的Mie散射特性Fig.3 The absolute values of T-matrix elements LL of l=0 for a hollow glass microsphere in unbounded polymer

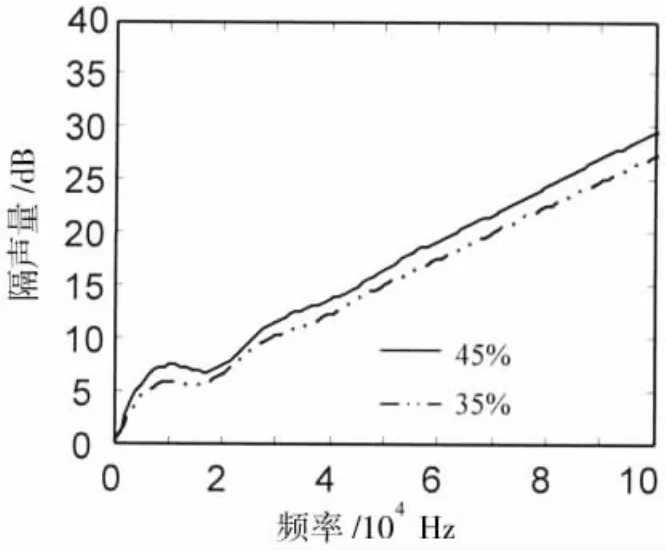
图4 空心玻璃微珠填充分数对复合材料声衰减性能的影响Fig.4 Effects of the filling fraction of hollow glass microspheres on the transmission loss of the polymer slab

3 结 论

在粘弹性聚合物中填充空心玻璃微珠可有效增加材料的声衰减。本文采用空心微珠周期分布简化模型和声子晶体领域发展的多重散射法，分析了填充空心玻璃微珠的聚合物复合材料的声衰减性能，理论计算结果与Baird等人的试验测试结果在各填充分数下相吻合，说明了算法的有效性。然后，采用Mie散射理论，分析了单个空心玻璃微珠在复合材料中的Mie散射特性，在文中分析频段，空心玻璃微珠主要通过调节介质等效阻抗和损耗来提高复合材料的隔声量，且复合材料声衰减随玻璃微珠填充分数的增加而逐步增大。

参 考 文 献：

[1]Sigalas M M,Soukoulis C M.Elastic-wave propagation through disorderd and/or absorptive layered systems[J].Phys.Rev.B,1995,51(5)：2780-2789.

[2]Majewski M,Kursa M,Holobut P.Kowalczyk-Gajewska K.Micromechanical and numerical analysis of packing and size effects in elastic particulate composites[J].Composites Part B：Engineering,2017,124：158-174.

[3]Dinzart F,Sabar H,Berbenni S.Homogenization of multi-phase composites based on a revisited formulation of the multicoated inclusion problem[J].International Journal of Engineering Science,2016,100：136-151.

[4]Baird A M,Kerr F H,Townend D J.Wave propagation in a viscoelastic medium containing fluid-filled microspheres[J].J Acoust.Soc.Am.,1999,105(3)：1527-1538.

[5]Schöneich M,Dinzart F,Sabar H,Berbenni S,Stommel M.A coated inclusion-based homogenization scheme for viscoelastic composites with interphases[J].Mechanics of Materials,2017,105：89-98.

[6]Haberman M R,Berthelot Y ves H,Jarzynski J,Cherkaoui Mohammed.Micromechanical modeling of viscoelastic voided composites in the low frequency approximation[J].J Acoust.Soc.Am.,2002,112(5)：1937-1943.

[7]谭红波,赵 洪,徐海亭.有限元法分析空腔周期分布粘弹性层的声特性[J].声学学报,2003,28(3)：277-282.Tan Hongbo,Zhao Hong,Xu Haiting.Sound characteristics of the viscoelastic layer containing periodic cavities by the finite element method[J].Acta Acoustic,2003,28(3)：277-282.

[8]Hladky-Hennion A C,Decarpigny J N.Analysis of the scattering of a plane acoustic wave by a doubly periodic structure using the finite element method application to alberich anechoic coatings[J].J Acoust.Soc.Am.,1991,90(5)：3356-3367.

[9]Sigalas M M,Kushwaha M S,Economou E N,Kafesaki M,Psarobas I E,Steurer W.Classical vibrational modes in phononic lattices theory and experiment[J].Z.Kristallogr,2005,220(9)：765-809.

[10]Zhao Honggang,Liu Yaozong,Wang Gang,Wen Jihong,Yu Dianlong,Han Xiaoyun,Wen Xisen.Resonance modes and gap formation in a two-dimensional solid phononic crystal[J].Physical Review B,2005,72：012301.

[11]Ivansson S M.Anechoic coatings obtained from two-and three-dimensional monopole resonance diffraction grating[J].Journal of the Acoustical Society of America,2012,131：2622-2637.

[12]Liu Z Y,Zhang X,Mao Y et al.Locally resonant sonic materials[J].Science,2000,289：1734-1736.

[13]Zhao H,Wen J,Yang H,Lv L,Wen X.Backing effects on the underwater acoustic absorption of a viscoelastic slab with locally resonant scatterers[J].Applied Acoustics,2014,76：48-51.

[14]Psarobas I E,Stefanou N,and Modinos A.Scattering of elastic waves by periodic arrays of spherical bodies[J].Phys.Rev.B,2000,62(1)：278-291.

[15]Liu Z Y,Chan C T,Shen P,et al.Elastic wave scattering by periodic structures of spherical objects：Theory and experiment[J].Phys.Rev.B,2000,62(4)：2446-2457.

[16]Liu Z Y,Chan C T,Shen P.Three-component elastic wave band-gap material[J].Phys.Rev.B,2002,65(16)：165116.

[17]Ruffa A.Acoustic wave propagation through periodic bubbly liquids[J].J Acoust.Soc.Am.,1992,91(1)：1-11.