球扁钢疲劳裂纹扩展的实验及数值预报方法

党之凡，乐京霞，毛文刚

（1.中国舰船研究设计中心，武汉 430064；2.武汉理工大学 交通学院，武汉430063；3.查尔姆斯理工大学，瑞典）

0 引 言

疲劳破坏是船舶与海洋工程结构物的主要破坏模式之一。球扁钢在船舶与海洋结构中已被广为使用，其在交变载荷作用下的疲劳裂纹萌生及扩展过程是评估结构疲劳性能的重要参考指标。然而，各国船级社颁布的船舶结构疲劳评估方法[1-3]大多以等效L型钢替代球扁钢作为疲劳破坏的研究对象，疲劳破坏依据不明确。另外，许多全尺度结构节点疲劳试验[4-6]也没有明确指出球扁钢的疲劳失效判据。上述原因往往导致结构疲劳寿命预报结果分散性大，结构的疲劳强度过于保守。在球扁钢的疲劳裂纹扩展过程中，掌握其表面三维裂纹形状的生长及变化规律，可为球扁钢的疲劳破坏提供判断依据，是准确预报结构疲劳寿命的必要前提。

应用无损探伤设备可以检测出球扁钢表面裂纹的深度从而得出裂纹前缘形状。目前已有的无损探伤方法有直流电压降法[7-8]、超声波检测法[9]和电磁感应测量法[10]。然而直流电压降法的测量值易受到裂纹侧面接触情况的影响从而产生偏差，超声波检测法难以区分裂纹所产生的回音和其他噪音，电磁感应测量法则需要相应的装置来产生磁场。同时，大多数研究[11-15]在计算裂纹扩展的时候都将裂纹前缘简化为一固定形状，从而将三维的裂纹前缘计算降为一个二维问题以得到一个合适的裂纹扩展规律。由于在拉压或弯曲疲劳载荷的作用下表面裂纹在扩展直至穿透失效的过程中会形成弧形前缘，有研究者认为该前缘可以用圆弧来代替，也有学者认为椭圆能更有效地描述裂纹前缘形状[16]。上述裂纹形状假设方法虽然能够简化疲劳计算，但与自然形成的疲劳裂纹仍有所差异。

鉴于上述原因，本文提出将应变片安置在裂纹表面张口上，以快速有效地测量球扁钢表面裂纹深度。文献[17]中已经推导出二维表面裂纹深度与裂纹张口位移之间存在一定的比例关系，但该比例系数随着裂纹体结构的不同而不同。因此，本文将上述方法应用于球扁钢三维表面裂纹的形状预测，通过有限元分析方法得到球扁钢裂纹张口位移与裂纹深度比例关系，在测得球扁钢裂纹前缘深度的基础上，得到其裂纹前缘形状。然后，应用经典Paris公式通过三维有限元通用数值分析方法对受弯曲疲劳载荷作用下的球扁钢表面裂纹扩展进行预测。最后，通过与试验结果对比验证测量与预测裂纹前缘方法的精度，为以后球扁钢失效判据的界定提供参考。

1 球扁钢表面裂纹形状预测方法

1.1 裂纹形状获取

线弹性断裂力学中已经给出在远处均匀受拉应力σ的“无限大”平板中心长度为L的Ⅰ型裂纹，其表面张口位移（COD）可由下式得出[18]：

式中：E为材料的弹性模量，x为沿裂纹开口长度方向。为消除载荷对裂纹开口的影响，定义名义裂纹张口位移NCOD为裂纹开口上每一点的张口位移COD与该处单位名义应变εn的比值（2）。

根据胡克定理：

故有：

由（4）式可看出“无限大”板中心Ⅰ型裂纹表面一点上的NCOD仅与裂纹长度L有关，且该类表面裂纹的NCOD沿裂纹呈椭圆分布。由公式（3），NCOD可改写为下式[19]：

式中：V为一仅与裂纹深度d和结构厚度T有关的常数。

根据前期研究[20]可知，NCOD沿裂纹开口的分布与裂纹深度近似地存在一个比例关系α，如下式所示：

所以，测量出NCOD沿裂纹的分布即可较为准确地得到表面裂纹深度的分布。使用应变片测量NCOD的原理如下图1所示，将应变片沿裂纹开口方向贴在裂纹表面上，图中应变片上实线部分表示试件在受拉时应变片所测得应变分布εc以及名义应变εn。如图1所示，在裂纹张口正上方应变数值εc将产生一个峰值，然后在离开裂纹尖端处急速下降到零。随着远离裂纹，其应变数值将慢慢回复到构件表面名义应变εn的大小。

图1 含表面裂纹试件应变分布Fig.1 Strain distribution on the measuring strain gauge surface

在实际使用应变片测量时，应变片的有效长度为le即为上述积分长度lc，同时应变片的输出应变为该段应变的平均值ε¯，故（7）式可简化为下式：

因此，名义裂纹张口位移NCOD可由下式获得：

故裂纹张口位移δ可以近似地由裂纹张口应变εc在lc上的积分所得到，如下式所示：

式中：s和sr分别为裂纹开口处以及参考应变位置到载荷作用点的垂直距离。

为证明NCOD值可以由上述方法获得，对含二维裂纹的悬臂梁进行了试验。试验试件为左端固定右端自由的悬臂梁（250 mm×30 mm×25 mm）。在其上预制宽度为0.1 mm、深度为d的二维裂纹，并在悬臂端用小锤敲击。试验设置如图2所示。

在试件预制裂纹正上方A点以及距A垂直距离为40 mm的参考位置B处各贴一有效长度lc=2 mm的应变片。预制裂纹深度为4 mm的试件经小锤敲击后各应变片输出电压如图3所示，应变片输出电压幅值与应变关系如（10）式所示。再根据（9）式即可得试件NCOD。

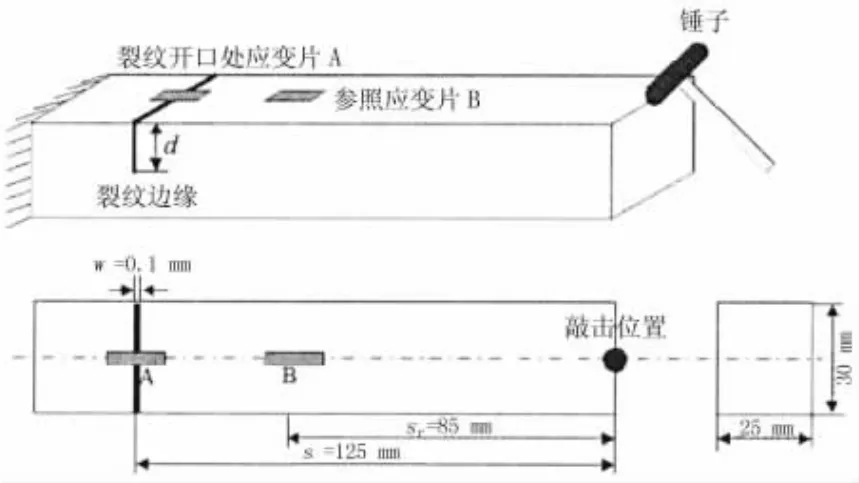
图2含二维裂纹悬臂梁试验设置Fig.2 Experiment setup on edge crack in flat bar

图4 显示了不同裂纹深度试件的NCOD测量结果，并且试验结果与有限元计算结果基本吻合。由此可知，在特定结构形式与材料下NCOD与裂纹深度之间的比例系数可由有限元方法获得。图5为应用有限元分析方法计算船用球扁钢HP260*10的NCOD与裂纹深度关系，其中，裂纹前缘为圆弧形，计算半径分别为15 mm，20 mm，25 mm和30 mm。

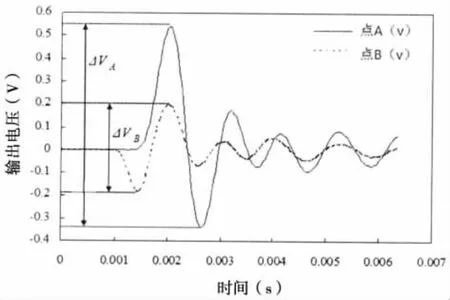
图3 应变片输出电压曲线Fig.3 Signal waves recorded from measuring strain gauges

图4 悬臂梁NCOD与裂纹深度关系Fig.4 Relation between crack depth and NCOD in cantilever bar

1.2 球扁钢疲劳裂纹扩展预测

大量的疲劳裂纹扩展试验均表明在裂纹扩展过程中，裂纹前缘并非一直保持同一固定形状[21]。表面裂纹扩展规律的研究主要包括两个方面的内容：一是裂纹扩展速率的描述，二是裂纹扩展形状变化规律的研究。对于表面裂纹的扩展速率，近年来随着实验研究的发展和有限元技术的应用，应力强度因子的求解基本上得到了比较一致的结果[22]。针对裂纹扩展速率的描述，目前国内外学者大多仍采用Paris公式来描述[23]。

在裂纹稳定扩展区域内，疲劳扩展速率da/dN与应力强度因子幅值ΔK之间存在如下关系：

式中：C和m是根据ASTM E647-88[24]使用标准试件获得的材料参数，本文研究的船用球扁钢的材料参数C和m分别取1.83×10-13和2.736。

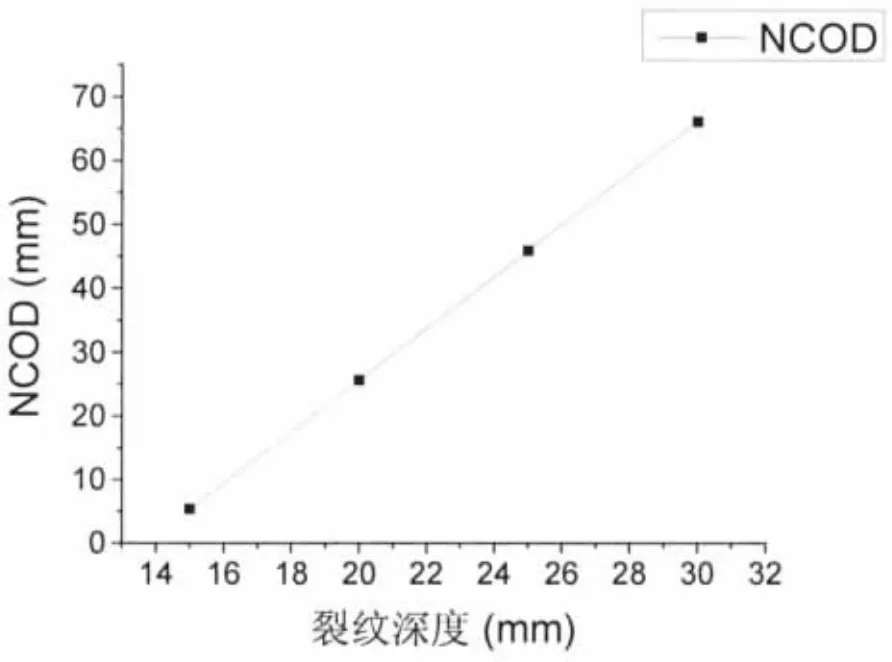
图5 有限元计算球扁钢NCOD与裂纹深度关系Fig.5 Relation between crack depth and NCOD in bulb-flat

由于球扁钢表面疲劳裂纹前缘通常为一条曲线，故裂纹前缘应力强度因子随着位置的不同而不同。因此Paris公式可改写为以下式形式：

假设疲劳裂纹扩展过程中最小疲劳载荷为0，则裂纹扩展步长Δai可由（13）式获得。为保证计算的足够精确度，Δamax通常在裂纹扩展模拟中保持为一个很小的常数。在本文研究中，最大裂纹扩展步长Δamax取为球扁钢球头厚度的1/250[25]，根据图6所示裂纹扩展方向，计算出裂纹扩展步长就可得出一系列裂纹扩展后的点，即可得扩展后的裂纹前缘线。

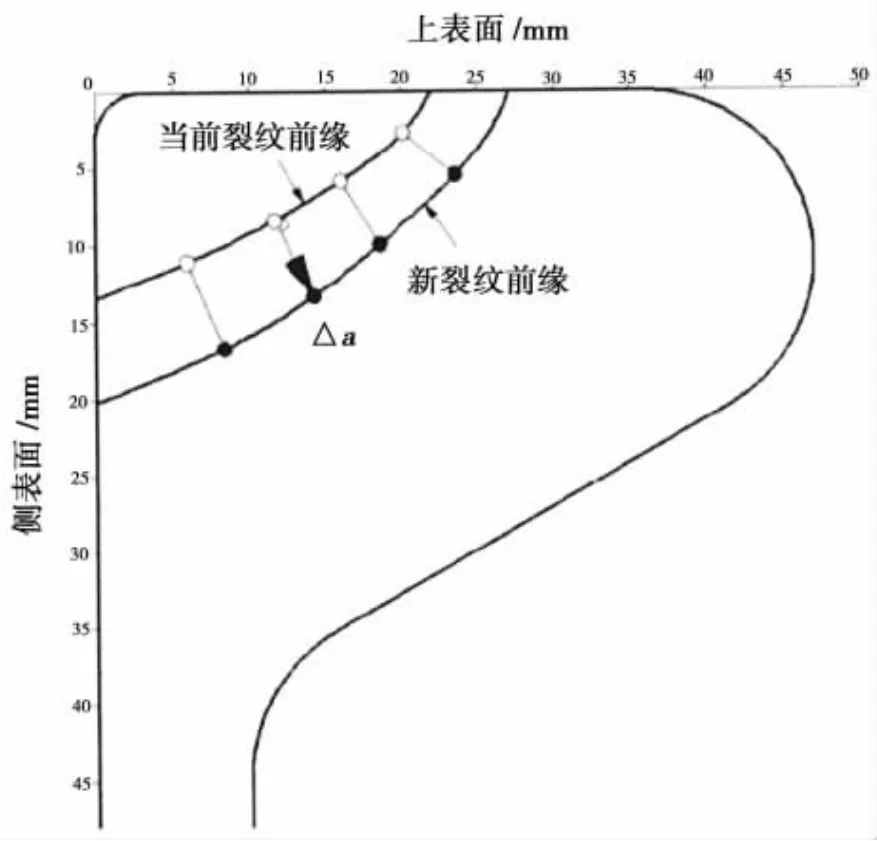
图6 球扁钢曲线裂纹前缘疲劳扩展Fig.6 Local fatigue crack growth along a curved crack front

图7 球扁钢表面裂纹有限元模型Fig.7 FE model for surface crack on the bulb-flat

应用有限元分析方法计算沿裂纹前缘分布的应力强度因子，球扁钢表面裂纹有限元模型如图7所示。

考虑到球扁钢球头厚度，认为其表面裂纹前缘应力应变状态为靠近试件表面为平面应力状态，其余为平面应力状态[26]。故采用（13）式运用有限元分析方法计算其裂纹前缘应力强度因子。

式中：G为剪切模量；ν为泊松比，取0.3；u1/4为有限元模型中1/4节点的张开位移；r1/4为1/4节点距裂纹尖端节点的距离。

2 CMOD测量试验

CMOD测量试验是基于1：1全尺寸模型疲劳试验的基础上进行的。由于承受船体梁总纵载荷时，船底纵骨球扁钢承受较大的船体梁载荷，而实肋板及横舱壁承受较大的横向载荷，故本试验选取载荷情况复杂，疲劳问题突出的船底纵骨穿过水密实肋板节点作为研究对象。并且根据文献[1]，纵骨与横向强框架和横舱壁的连接部位是明确规定的校核部位。

试验模型如图8所示，试件长度为4 920 m，2个强肋位；宽1 620 mm，为两个纵骨间距。纵骨贯穿实肋板节点分别为水密实肋板和非水密实肋板形式；深1 200 mm，至内底板。

考虑节点实际受力情况，试验试件中前后两端面均为刚性固定，垂向水密肋板上缘为加载端，使用加载仪器对试件施加垂向循环载荷，如图9所示。热点位置取位于肘板和纵骨相交焊趾处，具体定义如图9中所示。试验同时应用有限元（图10）计算各热点应力及名义应力，经静载试验及有限元计算得出最大应力处为热点4（HS4）。

图10 全尺寸疲劳试验有限元模型及热点 4（HS4）放大图Fig.10 FE model of the full-scale fatigue test&the fine mesh FE of the HS4

图11 球扁钢NCOD测量试验设置Fig.11 NCOD measurement experiment set-up for bulb-flat surface crack

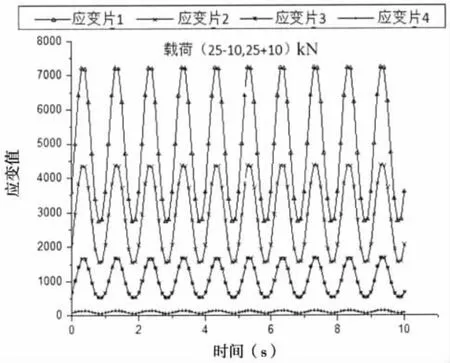
图12 4测点在25+10cos2π ft kN载荷下应变值Fig.12 The strain history of strain gauges under the loads of 25+10cos2π ft kN

图13 3测点NCOD值线性回归Fig.13 Linear fitting for the 3 gauges

疲劳试验载荷为45+40cos2π ft kN，载荷比R=0。在热点4处观察到疲劳裂纹表面长度生长到28 mm并且穿透球扁钢侧面时开始进行NCOD测量试验。试验设置如图11所示，在球扁钢侧面裂纹开口上布置三个应变片（应变片1～3）以测量裂纹开口位移（COD），并将参照应变片贴在旁边一侧以测量名义应变εr。

由于球扁钢疲劳裂纹扩展过程中其COD超过了应变片的测量能力，且根据裂纹闭合理论[27]，当试件所受应力低于裂纹张开水平下应力σop时NCOD与裂纹深度有良好的线性关系。因此，对试件进行一系列小载荷静载以及动载试验。图12所示为4个测点应变片在25+10cos2π ft kN循环载荷下所测实验数据。图13表明三个测点所测量的NCOD实验数据及其线性回归。

根据图5以及图13可得到疲劳扩展试验中三个测点处裂纹深度，经过样条曲线拟合得出裂纹前缘线如图14（a）所示；基于现有测点运用本文1.2节对球扁钢裂纹疲劳扩展进行预测，预测裂纹前缘线如图 14（b）所示。

图14 球扁钢表面裂纹前缘曲线Fig.14 Crack shapes of the surface crack on the bulb-flat

3 NCOD测量及疲劳裂纹扩展预测的试验比较

图15为试件球扁钢部分疲劳断裂后的裂纹剖面图，以球扁钢侧面为X轴、球扁钢上表面为Y轴，建立直角坐标系。疲劳裂纹前缘线如图中白色实线所示。

图15 球扁钢疲劳裂纹扩展剖面Fig.15 Fracture surface appearance of bulb-flat

图16 预测裂纹深度与实验结果比较Fig.16 Comparison between predicted and measured crack depths

NCOD方法测量所得裂纹前缘线以及预测裂纹扩展前缘线与疲劳试验结果对比如图16所示。由于每条预测裂纹均为试件表面两点与预测三点运用样条曲线拟合得出，故将每条曲线三个测点深度值与试件剖面裂纹前缘线对比得出其误差百分比。图中显示为8条裂纹前缘线的三个测点平均误差值。由图可知，各预测裂纹前缘最大误差均在3%以内，其中，采用NCOD方法测量裂纹前缘线形状误差值为1.4%，且最大测点误差在5%以内，故认为本文提出的方法能够测量及预测裂纹扩展前缘，并且和试验结果相比较，两者吻合较好。由此可表明运用本文方法测量及预测疲劳裂纹前缘线形状可行。

4 结 语

考虑到球扁钢是船舶和桥梁等钢结构中的纵向强力构件，掌握其疲劳裂纹扩展规律对准确预报结构疲劳寿命有着重要的意义。本文应用一种基于表面裂纹名义开口位移（NCOD）测量的简易方法，对全尺寸船用球扁钢三维疲劳裂纹形状进行预报；并利用Paris疲劳裂纹扩展公式，采用有限元数值分析方法，对裂纹扩展过程进行了预报。采用文中提出的方法能够较好地测量及预测裂纹扩展前缘，并与全尺寸船舶节点的疲劳试验结果相比较，方法具有一定的准确性。造成误差的主要原因有本文采用样条曲线对裂纹前缘点进行拟合；并且球扁钢裂纹扩展过程中，裂纹形状从类1/2椭圆形逐步扩展到类1/4圆弧形的过程中材料塑性区域的变化仍不明确。下一步工作将应用本文提出的疲劳裂纹扩展预报方法，为进一步研究球扁钢的失效判据提供参考依据。

参 考 文 献：

[1]中国船级社.船体结构疲劳强度指南[S].2015.China Classification Society.Guidelines for fatigue strength of ship structure[S].2015.

[2]Det Norske Veritas.Fatigue assessment of ship structures[S].2014.

[3]American Bureau of Shipping.Rules for building and classing[S].2015.

[4]Kim M H,Kang S W,Kim J H,Kim K S,Kang J K.An experimental study on the fatigue strength assessment of longiweb connections in ship structures using structural stress[J].International Journal of Fatigue,2010,32(2)：318-329.

[5]Fricke W,Paetzold H.Full-scale fatigue tests of ship structures to validate the S-N approaches for fatigue strength assessment[J].Marine Structures,2010,23(1)：115-130.

[6]Fricke W,Lilienfeld-Toal A V,Paetzold H.Fatigue strength investigations of welded details of stiffened plate structures in steel ships[J].International Journal of Fatigue,2012,34(1)：17-26.

[7]Tumanov A V,Shlyannikov V N,Kishen J M C.An automatic algorithm for mixed mode crack growth rate based on drop potential method[J].International Journal of Fatigue,2015,81：227-237.

[8]Doremus L,Nadot Y,Henaff G,Mary C,Pierret S.Calibration of the potential drop method for monitoring small crack growth from surface anomalies-Crack front marking technique and finite element simulations[J].International Journal of Fatigue,2015,70：178-185.

[9]Watanabe T,Trang H T H,Harada K,Hashimoto C.Evaluation of corrosion-induced crack and rebar corrosion by ultrasonic testing[J].Construction and Building Materials,2014,67(B)：197-201.

[10]Yusa N,Uchimoto T,Takagi T,Hashizume H.An accurately controllable imitative stress corrosion cracking for electromagnetic nondestructive testing and evaluations[J].Nuclear Engineering and Design,2012,245：1-7.

[11]卞如冈,崔维成,万正权,等.基于双参数统一方法的深海结构物疲劳裂纹扩展影响参数研究[J].船舶力学,2010,14(5)：516-525.Bian R G,Cui W C,Wan Z Q,et al.Effects of initial cracks and loading sequence on fatigue crack growth of the deepwater structures based on two-parameter unified approach[J].Journal of Ship Mechanics,2010,14(5)：516-525.(in Chinese)

[12]Wang F,Cui W C,Huang X P.Evaluation of surface crack shape evolution using the improved fatigue crack growth rate model[J].Journal of Ship Mechanics,2011,15(6)：660-668.

[13]周太全,陈鸿天.具初始裂纹钢桥梁焊接构件疲劳裂纹扩展和疲劳寿命计算[J].船舶力学,2009,13(1)：91-99.Zhou T Q,Chan T H T.Fatigue crack growth and fatigue life evaluation for welded steel bridge members with initial crack[J].Journal of Ship Mechanics,2009,13(1)：91-99.(in Chinese)

[14]Liu G,Gao M,Huang Y.Effect of nonlinear distribution stress on surface crack growth at welded joints[J].Journal of Ship Mechanics,2014,18(3)：291-302.

[15]Sjao W J.Effect of initial crack size on probability of fracture failure[J].Journal of Ship Mechanics,2001,5(6)：50-54.

[16]Lin X B,Smith R A.Shape growth simulation of surface cracks in tension fatigued round bars[J].International Journal of Fatigue,1997,19：461-469.

[17]Yue J,Fujimoto Y,Setyanto T A.Estimation of surface crack depth based on measurement of crack opening deformation[C].The 15th International Offshore and Polar Engineering Conference,2005：360-367.

[18]Broek D.Elementary engineering fracture mechanics(4th Edition)[M].Netherlands：Kluwer Academic,Dordrecht,1982.

[19]Okamura H.Introduction of linear fracture mechanics[M].Baifukan Co.Ltd.,Tokyo Japan,1976.

[20]Yue J,Wu W.Depth estimation for surface cracks based on crack mouth opening displacement measurement[C].The 20th International Offshore and Polar Engineering Conference,2010：20-25.

[21]Choi D H,Choi H Y,Lee D.Fatigue life prediction of in-plane gusset welded joints using strain energy density factor approach[J].Theoretical and Applied Fracture Mechanics,2006,45(2)：108-116.

[22]Carpinteri A,Brighenti R.Part-through cracks in round bars under cyclic combined axial and bending loading[J].International Journal of Fatigue,1996,18(1)：33-39.

[23]Paris P C,Erdogan F A.Critical analysis of crack propagation laws.Trans.ASME J Basic Eng[J].Journal of Fluids Engineering,1963,85(4)：528-534.

[24]ASTM.Standard test method for measurements of fatigue crack growth rates[S].2008.

[25]Lin X B,Smith R A.Fatigue growth simulation for cracks in notched and unnotched round bars[J].International Journal of Mechanical Sciences,1998,40：405-419.

[26]党之凡,乐京霞,董 岩,等.厚钢板疲劳裂纹扩展前缘应力状态试验与数值仿真[J].中国舰船研究,2016,11(2)：51-57.Dang Z F,Yue J X,Dong Y.Investigation on the stress state along crack front in fatigue crack growth rate test for thick high strength steel plate[J].Chinese Journal of Ship Research,2016,11(2)：51-57.(in Chinese)

[27]Elber W.Fatigue crack closure under cyclic tension[J].Engineering Fracture Mechanics,1970,2：37-44.