模型、联想、转化：数学解题创新的关键点*——2009年全国高中数学联赛陕西赛区预赛一道几何题的证明

陕西安康学院数学与统计学院 (725000) 赵临龙

命题1 (2009年全国高中数学联赛陕西赛区预赛试题)[1]如图1，PA、PB为⊙O的两条切线，切点分别为A、B，过点P的直线交⊙O于点C、D，交弦AB于点Q，求证：

PQ2=PC·PD-QC·QD(1)

参考答案利用圆幂定理、相似性、共点圆等知识，给出证明，其技巧性要求较高.

现在，通过圆幂定理：PA2=PC·PD，QC·QD=QA·QB，将命题1结论，转化为PQ2=PA2-QA·QB(2)

图1 图2 图3

此时，想到斯库顿(Schooten)定理：如图1，若PQ为△PAB的内角平分线段，则PQ2=PA·PB-QA·QB(3)

在图1中，尽管PA=PB，但PQ不是△PAB的内角平分线段，(3)不成立.

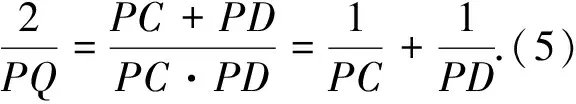
由上题的结论，又使我们想到蝴蝶定理.

命题2(蝴蝶定理)[3]如图2，过⊙O内一弦EF中点P引任意两弦AB、CD，AD和BC交EF于Q1、Q2，则Q1P=Q2P.

当点P在弦EF延长线上时，有坎迪(Candy)蝴蝶定理.

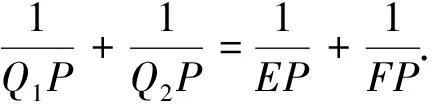
如图3,当割线PAB、PCD退化为⊙O的切线，则弦AD与BC合于一条，及点Q1、Q1合于切点弦与EF的交点Q，则命题3退化为命题1.

也就是说，可以用蝴蝶定理证明命题1.由此，我们说：模型、联想、转化是数学解题创新的基本环节.

如我们以斯库顿定理为模型，需要构造△PCF，使PF=PD.

如图4，将割线PCD沿对称轴PO对折得割线PEF，连线FC和ED的交点R在对称轴PO上，而且可利用射影几何证得：[4]点A,R,B共线.*

图4 图5

由斯库顿定理，得R2=PC·PF-RC·RF=PC·PD-RA·RB=PC·PD-(QA-RQ)·(RQ+QB)=PC·PD-RQ(QA-QB)+RQ2-QA·QB=PC·PD-2RQ·RQ+RQ2-QC·QD(6)，则PC·PD-QC·QD=R2+RQ2=PQ2(由AB⊥PO)(7).

*附录：极点与极线的理论

定义[4]如图5，过点P引二次曲线Γ的直线PAB交Γ于A、B两点，若直线PAB上一点Q满足：

特例：当点P在Γ上，则过P与Γ相切的直线为极点P关于Γ的极线.

结论:二次曲线Γ极线l的点列Q与过极点P的线束l'构成一一对应.

此时，在图4中，取完全四边形CDEF，则对角线的交点R的极线必过完全四边形CDFE对边交点P，又⊙O两切点A、B的两切线也交于点P,于是⊙O的极点A、R、B三点共线.