一道几何竞赛题的多角度探究
2018-07-30北京市第十二中学高中部100071杨雪芹高慧明
北京市第十二中学高中部 (100071) 杨雪芹 高慧明
题目如图1所示,在四边形ABCD中,已知∠ACB=∠ADB=90°,AC与BD交于点E,AC=BC,AD=4,BD=7,则S△ABE=___________.(2014年北京市高一数学竞赛预赛试题)
这是一道求解一般三角形面积的试题, 细细琢磨,这道题实际上可以从多个角度突破.通过分析,AD,BC分别可作为BE和AE边上的高, 并且AD,BC的长度已知. 如此一来,求面积问题就转化为求边长问题.所以BE或AE的长度求解就是解决该问
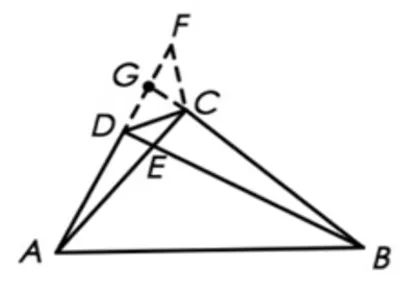
图1
题的关键之所在.
以下分别利用相似三角形、两角和的正弦公式、托勒密定理、余弦定理、四点共圆、面积的比等知识求出BE或AE的长,继而产生5种不同思路解决该问题.
首先,由已知条件容易得到的数量有
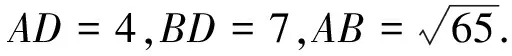
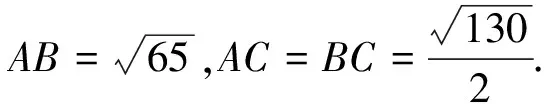
下面,我们从5个不同的角度作后续处理.
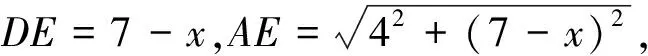
点评:把问题解决的关键量设为未知量,找出未知量满足的方程,转换为解方程问题.利用“方程的思想”处理几何问题.
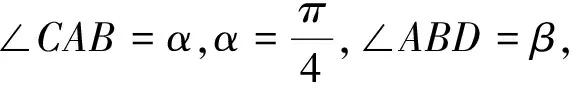
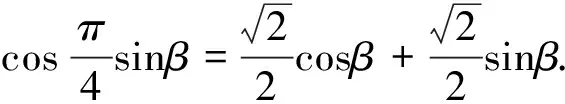
点评:利用角之间的关系,“设而不求”,不求出具体的角,只求出相应角的三角函数值,利用直角三角形和已知条件求出边长.
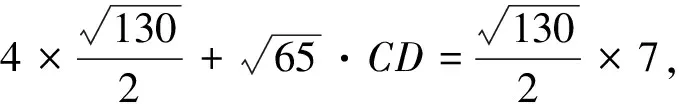
点评:托勒密定理(Ptolemy)定理指出:圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积.从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.该解法应用四点共圆、托勒密定理解决问题.
解法4:(利用全等、共圆、线段比例)延长AD到F,使DF=3,AF=7,于是AF=BD,AC=BC.
由已知得∠DAC=∠CBD.所以△ACF≌△BCD.所以CD=CF.在四边形ABCD中,∠ADB=∠ACB=90°,所以A,B,C,D四点共圆.
由圆内接四边形的外角等于内对角得∠CDF=∠ABC=45°.所以△DCF是等腰直角三角形.
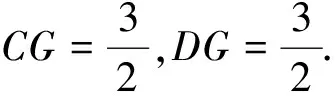
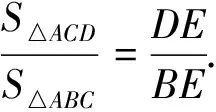
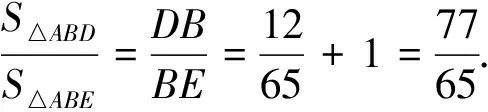
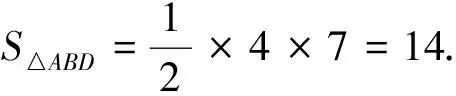
点评:这是一道高一的数学竞赛题,解法4和解法5采用高一学生熟悉的初中平面几何问题的处理方法,作辅助线,构造全等关系,利用线段成比例或三角形面积比解决问题,较之前三种方法,学生容易想到,但构造过程和解题过程相对麻烦.解法1和解法2较为简便.作为参加数学竞赛的学生,解法3中的知识也应该掌握,学会应用平面几何中的著名定理(梅涅劳斯定理、塞瓦定理、托勒密定理和其推广、西松姆定理)解决问题.
