浅谈中学数学教学中的德育功能
2018-07-30广东省广州市第七中学510080陈世明
广东省广州市第七中学 (510080) 陈世明
十九大报告指出,要落实立德树人的根本任务,“才者,德之资也;德者,才之帅也”.教育部最新(2017年8月17日)发布的《中小学德育工作指南》中又指出:“充分发挥课堂教学的主渠道作用,将中小学德育内容细化落实到各学科课程的教学目标之中,融入渗透到教育教学全过程”.“严格落实德育过程.按照义务教育、普通高中课程方案和标准,上好道德与法治、思想政治课,落实课时,不得减少课时或挪作它用”.“发挥其它课程德育功能.要根据不同年级和不同课程的特点,充分挖掘各门课程蕴含的德育资源,将德育内容有机融入到各门课程教学中”.“数学、科学、物理、化学、生物等课要加强对学生科学精神、科学方法、科学态度、科学探究能力和逻辑思维能力的培养,促进学生树立勇于创新、求真求实的思想品质”.在中学数学教学中如何挖掘、渗透德育功能,是当今数学教学中值得研究的一个课题,本文对此做初步探讨,敬请各位专家指教!
1.在定理教学中培养学生求真求实的思想品质
众所周知,逻辑性、严谨性、抽象性是数学学科的三大特征.为了降低学习难度,新课程中对许多定理的证明不作要求,然而,我们在教学中发现,许多老师在教学此类定理时,不仅既不讲此类定理的证明也不探究此类定理的生成过程,而且对此类定理为真所必要的说明也只字不提,只是将此类定理中的一些关键字词抽出来“一填了之”,然后就是大规模的定理应用(笔者所在区的一次区公开课上,授课老师就是这样处理的).事实上,按新课程标准,对此类定理不要求证明,并不等于不作说明,若对此类定理为真所必要的说明也没有了,那么数学就变成了一门不讲理的学科了,这样的数学教学不仅失去了对学生求真求实的思想品质的培养良机,而且也是十分危险的!“直线与平面平行的判定定理”是空间直线与平面的位置关系的第一个定理,新课标教材对这一定理的证明不作要求,笔者在教学这一定理时是这样处理的:
师:要判定直线a与平面α平行,只要判定——
生:直线a与平面α没有公共点.
师:那如何判定直线a与平面α没有公共点呢?(学生一脸茫然,不知所措!大约1分钟后)
师:不好办吧!请同学们回忆一下,我们已经知道直线a与“α”一定是没有公共点的?(大约1分钟后)
生1:直线a与和它异面的直线b一定是没有公共点的或直线a与和它平行的直线b也一定是没有公共点的!
师:很好!这样一来,我们不妨大胆的来猜一猜:若直线a与平面α内的一条直线b异面,能否推出直线a与平面α没有公共点?
生(部分):能吧?
生(部分):不能!
师:生2你来说一说为什么不能?

图1
生2:这很简单,举一个反例就成了!如图1,a与b是异面直线,但a与α有公共点.
师:真妙!要否定一个结论,只要举一个反例就成了.同学们清楚了吗?
生:清楚了!
师:若直线a与平面α内的一条直线b平行呢?又能否推出直线a与平面α没有公共点?(巡堂发现:同学们在画各种图形,也想举一个反例来否定上述结论,但均没有成功,大约2分钟后)
生:能!(很肯定的)
师:为什么?
生:没有找到反例!
师:没有找到反例就能说明直线a与平面α没有公共点?假若那样的反例大家都没有找到呢?
生:是啊!
师:因此,要肯定一个结论,一定要说明理由才行!生3,你来说说理由看?

图2
生3:还没想好!(其余同学在积极思考)
师:如图2,由a∥b,可推出什么结论?
生3:过a,b可确定一个平面β.
师:很好!大家看,在确定了平面β后,直线a与平面α就“天各一方”(学生大笑)!但它们并不“孤单”(学生又笑),因为α与β有一条公共直线b相连,真所谓“天各一方——一线牵”啊!这样一来,要说明直线a与平面α没有公共点,只要说明——
生:直线a与直线b没有公共点即可!而a∥b,所以直线a与直线b没有公共点,从而直线a与平面α没有公共点,故a∥α.
师:太好了!这样一来,我们就得到了一个什么结论?
生:如果直线a与平面α内的一条直线b平行,那么直线a与平面α平行.

图3
师:如图3,也能推出a∥α吗?
生(恍然大悟的):不能!
师:没想到吧!前述结论应修改为——
生:如果平面外的一条直线与平面内的一条直线平行,那么这条直线与这个平面平行.
师:很好!这就是我们今天要学的“直线与平面平行的判定定理”(下面的课从略).
在上述定理的生成过程中,从学生熟知的“直线a与和它异面的直线b一定是没有公共点或直线a与和它平行的直线b也一定是没有公共点”出发,通过“猜想——实验(画图)——概括”等过程,比较自然的得出结论.尤其是通过“天各一方——一线牵”的“艺术化”处理后,定理为真的事实已一目了然,对定理是否再需证明已不是很重要了.
所谓“求真”,就是“求是”,亦即实事求是去认识事物本质,把握事物的规律;“求实”则是在对这种规律的指导下,去做、去实践.一个数学定理往往需经合情推理的发现,再经演绎推理的证明才能获得,尤其是课本中不要求证明的定理,其证明往往是比较复杂的,教学中,通过揭示此类定理的生成过程,对培养学生求真求实的科学态度,培养和锻炼学生的探究能力和思维品质有更大的作用和意义.
2.在公式教学中锻炼学生科学探究能力和创新意识
李克强总理最近(2018年1月3日国务院常务会议)突出强调理论数学等基础学科对于原始创新能力的重要意义,他还指出“数学等基础学科研究要着眼于未来,但必须从教育抓起”.中学数学教学任重道远,同时也倍受鼓舞,在中学数学教学中,培养和锻炼学生科学探究能力、逻辑思维能力和创新能力的例子很多,尤其在公式教学中.这里仅举一例:
师:有一天,甲同学来问我这样一个问题:cos15°=cos(60°-45°)=cos60°-cos45°为什么不对?说实话,甲同学还很不错,知道这一等式是不成立的,同学们你们是否也知道?
生:知道!
师:为什么?说说理由看?
生:因为cos15°>0,而cos60°-cos45°<0,所以等式不成立.
师:很好!这样一来,我们达成了一个共识:cos(60°-45°)≠cos60°-cos45°.那么cos(60°-45°)究竟等于多少呢?(学生陷入沉思中!)
师:cos(60°-45°)是一个三角函数问题,在前面第一章我们已学习了三角函数的有关知识,能否有公式可用?
生:好像没有!
师:除了前面第一章我们已学习了三角函数的有关知识外,我们还学过其它的三角函数知识没有?
生:在初中还学过解直角三角形!
师:好的!既然在第一章的三角函数里没有公式可用,那么,我们不妨就到直角三角形中去看一看!你能否画出一个角为60°的直角三角形?
生:太容易了!

图4
师:是吗?那我就来画一个RtΔABC,使得∠A=60°,∠C=90°,如图4,在这个RtΔABC中,你还能作出一个45°,同时还出现15°的角吗?
生1:很好办!以A为顶点,AB为一边,在RtΔABC中作∠BAD=45°交BC于D,则∠DAC=15°.
师;你真行!在这个直角三角形中,能否得出cos15°呢?
生2:很简单!在RtΔACD中,AC=ADcos15°.
师:在RtΔABC中,还可得出AC=?
生2:AC=ABcos60°.
师:这样就有ADcos15°=ABcos60°.现在要求cos15°,若在这一等式的右边也出现AD,那么,两边同约去AD,即可求出cos15°,下面怎样才能使等式的右边也出现AD呢?(学生又陷入沉思中!大约2分钟后)
生3:老师,可不可以这样做?
师:怎么做?请讲!
生3:(生3口述,老师板书)在图4中,过D作DE⊥AB于E,则由ADcos15°=ABcos60°得:ADcos15°=(AE+BE)cos60°=ADcos45°cos60°+BEcos60°=ADcos45°cos60°+DEcot30°cos60°=ADcos45°cos60°+ADsin45°cot30°cos60°,所以cos15°=cos45°cos60°+sin45°cot30°cos60°.
师:太妙了!(这时教室里响起了热烈的掌声,同学们也有大功告成之感!)上述结果完全是正确的,但形式太“丑”了,说得不好听一点,简直是“丑不可言”!(学生感到很突然,教室里立即鸦雀无声),你们看,等式右边的第一项是二项积,而第二项则是三项积,不和谐吧!更“可恶”的是:左边实际上是cos(60°-45°),只与60°,45°有关,与30°无关,而右边的第二项竟然冒出一个30°,这个“30°”岂不是来添乱吗?
生4:那就把它化掉吧!
师:好的,生4,你来试试!
生4:(上台)通过化简得出:cos(60°-45°)=cos60°cos45°+sin60°sin45°①
师:等式①的确优美多了!当然①式也还不太和谐——
生:左边是“-”,而右边是“+”.
师:很好!这也正好说明世上并没有“十全十美”的事物(到此,同学们松了一口大气,大有洋洋得意之感!),这时——
师:你们别高兴太早!刚才甲同学是将cos15°化成cos(60°-45°),我们帮他解决了;
若乙同学是将cos15°化成cos(45°-30°),而丙同学是将cos15°又化成cos(135°-120°)呢?…,我们是不是一一帮他们去解决?
生:不!
师:那怎么办?总不能“见死不救”吧!
生5:让他们自己按上述方法去解决.
生6:老师,我们能否得出一个一般的公式?免得每次都这样去做,太烦了!
师:这个想法好!得出一个怎样的公式?
生6:是否对任意的α,β∈R,都有cos(α-β)=cosαcosβ+sinαsinβ②
师:很好!你是怎样想到的?
生6:我是根据上述①式猜出来的!
师:真不错!不过,猜出来的结论不一定正确,你能证明它成立吗?
生6:还没有想好!
师:好的!请继续思考.有谁能证明②式?(同学们在积极思考,大约1分钟后)
师:能否仍按前面作直角三角形的方法去证?
生:不能?
师:为什么?
生:因为α,β不一定能成为直角三角形的一个内角.
师:很对,不过不要否定得太快!虽然现在不能作直角三角形了,但前面的那种证法中所用的思想方法说不定还有用呢!所以不能“过河拆桥”,要学会“感恩”!下面我们一起来反思上述解法的关键点在哪里(与学生一起反思上述解法的每一步).
师:生7,你来说一说上述解法的关键点在哪里?
生7:算两次!就是把“AC”算了两次,第一次得出AC=ADcos15°,第二次得出AC=ABcos60°,这样就得出了关于cos15°的一个方程,然后通过解方程就得出了cos15°,也就是cos(60°-45°)的值.
师:说得太好了!上述解法实际上应用了“算两次”的思想方法,你们还在哪里也用到过这一思想方法?
生:在《平面向量》里也用过.
师:对啊!“算两次”是一种重要的解题思想方法,不仅过去用到,现在用到,而且将来还可能用到!下面再回到②式的证明,怎样才能证明它呢?
生8:老师!是不是还是用“算两次”?
师:怎么算?
生8:还没想好!
师:请再想一想.有谁想到了吗?(大约1分钟后)
师:前面说了,在第一章三角函数里已没有公式可用,又不能用作直角三角形的方法,那怎么办?换句话说,现在进是进不了了,进不了就——
生:退!

图5
师:退到什么地方去呢?这是一个三角函数问题吧!那三角函数是从什么地方出发的?
生:单位圆!退到单位圆中去.
师:好的!那就到单位圆中去看一看,如图5,在单位圆中,设α,β的终边与单位圆分别相交于P,Q两点,由三角函数的定义得P(cosα,sinα),Q(cosβ,sinβ),请大家观察②式的右边,它恰是——
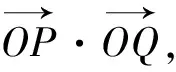
师:那②式的左边等于——
从而有cos(α-β)=cosαcosβ+sinαsinβ.
生:原来如此!
师:果然又用到“算两次”!但③式一定正确吗?
生:正确!
生10:还不一定吧?
师:为什么?
师:好极了!遇事要冷静,不要被一时的成功冲昏头脑,考虑问题应全面,接下来该怎么办?
生:分情况讨论!(这里从略)
师:这样一来,我们就证明了②式,有了这一公式,要算两角差的余弦就很方便了,这一公式也就是我们今天要学习的“两角差的余弦公式”(下面的课从略).

公式是构成整座数学大厦的支柱之一,加强对公式的探究教学,不仅是新《数学课程标准》对我们每位老师的要求,也是培养创新型人才、提高教学质量的必由之路.
3.在解题教学中塑造学生诚信做人、理性做事的优良品德

图6

此题在用向量法求解的过程中有一个关键步骤,就是求出点A和F的坐标后,根据条件计算点H的坐标.笔者当时是用“近朱者赤近墨者黑”来提示学生直接写出H点的坐标的,在得到笔者的提示后,学生很容易地理解了笔者所要表达的意图,问题很快解决.通过这个例子和经过笔者的进一步提示,学生对传统文化中的“中庸之道”有了更加理性的认识,上例中的点H的坐标不能用中点坐标公式简而求之,而是在类比中点坐标公式“取得平衡”的思想中将两端点的坐标各取一定的比例系数来求得.中庸并非“正中间”,而是不偏不倚的“中”,做人之道便是至诚至信、公平待人.在解题教学中,要让学生既领悟到数学的知识与方法,也更加理性地体会到中国传统文化中关于做人的道理,一举两得.

图7


要求出SΔBDE,由已知条件,应“脚踏实地”地去计算出ΔBDE的三边长,而当算出ΔBDE的三边长后,“奇迹”发生了,原来ΔBDE为直角三角形,从而问题简单获解.
“机会是留给有准备的人的”,本题中,若没有前期“脚踏实地”地计算的准备,就没有后来简单获解的机会.在这里“求距离”是最终目标,为了实现这个目标,我们必须先“脚踏实地”地进行计算和推理,这一思维正是我们做许多事情时应有的方法和态度.
在数学的发生与发展过程中,知识的形成与演变、重要思想方法的确立与发展、重大理论的发现与沿革等,其本身充满着唯物辩证法的思想.而在高中的数学教学中,面对一群理性精神的形成正处于关键期的高中学生,教学中尽可能多地发挥数学的学科特性,通过培养理性思维与分析问题、解决问题的能力培养学生诚信做人与理性做事.同时,在塑造学生正确的人生观、世界观和价值观及用理性的思维看待事物时,使学生更深刻地理解数学的方法和理论,让学生更加主动地端正学习态度,提高数学能力.德育与数学教学相辅相成,本身也是一个辩证的关系.
