智能转化“有且只有”生成自然解法
2018-07-30江苏省太仓市第一中学215400朱建良
江苏省太仓市第一中学 (215400) 朱建良
《数学课标(2011)版》指出“注重结合具体的学习内容,设计有效的数学探究活动,使学生经历数学的发生发展过程,是学生积累数学活动经验的重要途径”.教师在教学设计中应基于课标要求和教材内容,依据学情,因材施教,提供丰富的数学思维活动素材,帮助学生提升几何图形直观和合情推理能力,笔者尝试立足于帮助学生从函数观点、运动观点理解“有且只有”的数学涵义,在系列探究活动中明白数学思维之道,优化解题之术,优化数学思维品质.
数学是一门严谨的学科,在语言表达上严格要求准确规范、准确传达意思,笔者尝试以“有且只有”数学语言为几何探究主线,以函数、方程等几何核心知识和性质为载体,结合抛物线问题背景,由点到线,再及面,提炼共性,探求多题通解,尝试衍生变式问题,意在指向数学内涵与本质展开讨论,请同行指正.
1.解读内涵,明确任务
我们初学几何时,学习了几何基本事实:“在平面上,过两点有且只有一条直线”, “在同一平面内,过一点有且只有一条直线与已知直线垂直”等.“有且只有”是由“有一个”与“只有一个”复合而成的,其中“有一个”说明对象是存在的,“只有一个”说明对象是唯一的,所以“有且只有一个”说明对象有“存在性”和“唯一性”.
数学语言“有且只有”的相关数学问题蕴含了初中数学核心知识,如:函数、方程、距离与坐标关系,直线与圆的位置关系等,同时以“有且只有”为问题情境的数学问题突出了对学生运算,图形直观判断,演绎推理等多种能力的考查.
笔者在初中九年级数学教学过程中,尝试以抛物线问题情境下的“有且只有”问题为数学思维的载体,结合二次函数、方程、相似三角形、圆等核心知识设计问题,引导学生思考:(1)解决此类问题的难点是什么?(2)关键是什么?(3)解决问题运用了哪些数学基本方法?运用了哪些基本概念和原理?此类问题如何变式推广?(4)如何在正确理解各变量之间关系的基础上,建立合理的数学模型,解决问题?通过专题探究活动,深入抛物线及相关问题核心,优化学生数学理性思维品质.
2.剖析方法,揭示本质
尝试在课堂教学中运用启发性教学原则,引入“形”的观察,给学生研究数学问题带来直观的空间感受.引导学生体验数学方法对“有且只有”意境的解释,从细节入手,深刻领悟“有且只有”所要满足条件的内涵,挖掘有效的转化策略,自然、真实地展开数学发散思维,唤起学生欲发现、想探究、思创造的愿望.
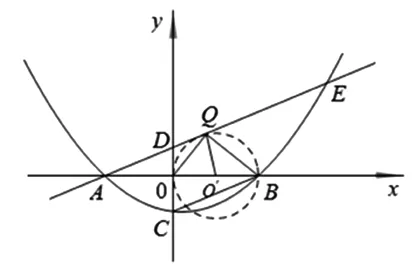
图1
问题1 如图1,抛物线y=k(x+1)(x-3k)(k>0),与x轴分别交于A、B两点,与y轴交于C点,连接BC,过A点作AE∥CB交抛物线于E点,若在直线AE上有且只有一点Q,连接OQ、BQ,使OQ⊥BQ,求k的值?
问题启智:(1)如何由“有且只有一点Q”联想几何模型,转化OQ⊥BQ?(2)如何从不同角度分析、联想,实现点的坐标与线段长度之间的转化?(3)如何捕获图形隐含的相似三角形,寻求图形运动过程中不变的数量关系?

设计意图:对特定的数学语言“有且只有”转化在几何图形中,在“数形结合”的角度重新审视分析问题,在建立数学模型,类比转化的探究过程中,提升学生的自主归纳和数学语言的互译转化能力.
3.理清关系,讲清道理
数学是思维的科学,寻求问题的解法,只能由学生自己感悟,学生在仔细观察、思考中疏理相关知识点,由表及里,逐层深入,透过现象审视几何图形的直观,剖析由特殊点对应的数量关系,逐步弄清问题的关键所在,明晰解题思路.

图2
拓展如图2,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于C点,M为抛物线顶点,直线MD⊥x轴于D点,点N为线段MD上一个动点,以N为等腰三角形的顶角顶点,NA=NG,等腰ΔNAG,G点落在直线CM上,若在直线CM上满足条件的G,有且只有一个时,求点N的坐标.
问题启智:(1)如何构建辅助圆?类比转化问题?(2)“点G有且只有一个”,如何在“形”的描述上直观刻画?(3)如何合理分类,避免漏解?


图3
如图3,“有且只有一个G点”还可理解为,以AN2为半径作⊙N2,RtΔAGK中,有N2A=N2G=N2K,而A、N2、K三点一直线时,不能构成三角形,此时N2(1,3),K(3,6).
设计意图:把所讨论的点进行数量和位置上的锁定,锁定在辅助圆上,确保结果不漏解,由抽象到具体,直观的辅助圆帮助学生充分感受特殊点之间的内在联系,提升了学生的理解能力.
4.类比迁移,拓展延伸
由特殊动点衍生特殊图形面积问题展开探究,深刻理解“有且只有”的特定涵意,直观感知由量变到形变的内在规律,从而掌握如何确定量的关系特征,在形的“变化”中找到“不变”的特征量,以外显寻求动点发展内涵的数学思维,再把此问题类比拓展,把探究活动经验升华为分析问题和解决问题的能力.

图4

问题启智:(1)如何把动点P的特殊位置直观转化为不等式的讨论区间?(2)如何理解动点P“有且只有一个”与“有且只有两个”的区别?(3)如何设未知数,用数量关系描述图形面积的变化规律?

设计意图:类比探究抛物线背景下的特殊三角形的面积问题,在对比疏理中解有所悟,理解“有且只有两个动点P”的一般转化思路,避免学生形成思维定势,加深了学生对几何图形面积最值问题与一元二次方程等知识的深层理解,有效训练了学生思维的敏捷性.
5.启迪思维,探求规律
深入浅出,把抽象的问题具体化,把复杂的问题最大限度地简单化,这是数学教学的真谛,通过学生归纳、猜想、推理证明,引导学生体验感悟数学分类讨论、特殊与一般、化归的数学思想方法,挑战数学思维的深度和发散性,揭示问题的本质和规律,引导学生转换视角,学会灵活处理“有且只有”相关问题.

图5
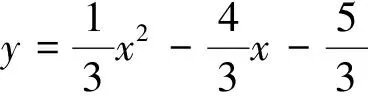
问题启智:(1)如何借助图形的直观性,突破难点,理解“有且只有两个动点Q”?(2)如何联系数学最值问题构造几何模型,求解ΔQCA面积的最大值?(3)如何揭示此类面积最值问题的深层思维结构?疏理出一般解题规律?


设计意图:由直线与抛物线的交点衍生出分类讨论的特殊三角形面积问题,演绎了用函数思想解决相关“有且只有两个动点Q” 问题的策略,帮助学生深刻理解变化图形的内在特征,积累解题经验,洞察问题本质,学会建模,善于转化.
通过抛物线背景下动点问题的系列探究活动,帮助学生学会在直线与抛物线的交点上做文章,巧妙转化,发展了学生的建模能力,帮助学生掌握了借助函数图像使抽象的“有且只有”问题形象化、直观化,实现数学思维可视化,解题过程条理化,因此“数形结合”是解决此类问题的关键.
数学教学过程应重视学生有效的思维活动,探究活动设计必须有一个专题,有一个明确的学习目标,本案例设计了一个有价值的数学语言转化的探究活动,为学生提供了一个数学问题情境和可供学生进行有效活动的抛物线背景的序列问题,并运用问题意识激发学生强烈的学习愿望,在探究抛物线问题中的特殊动点问题的变化规律过程中,帮助学生深刻、精准理解“有且只有”的数学涵意,训练学生的分析、综合、概括、判断、推理等初步逻辑思维能力由低级向高级逐步提升,提高了数学教学设计的有效性,提升了学生的数学素养.
