基于学力发展的“四种命题”教学设计与思考

江苏省张家港市崇真中学 (215600) 童先峰

1.教学背景

每年的11月，都是我市教育局组织的全市中小学、幼儿园课堂教学改革经验交流主题月，今年的活动主题是“发现教学智慧，发展学生学力”.活动要求课堂展示的教师要充分体现个人教学主张或个人学习课堂的品质，能体现互联网+背景下的学习课堂特色.笔者今年正好任教高二，结合教学进度等统筹考虑，选择了《四种命题》这个课题进行了如下设计.

2.基本情况

2.1 授课对象

本课为借班上课，学生系四星级高中江苏省梁丰高级中学2016级高二(6)班，该班为理科物生班，学生思维活跃，基础较好，善于总结归纳，有一定的逻辑推理能力，能够判断一些简单命题的真假.

2.2 教材分析

本节内容选自普通高中课程标准实验教科书(苏教版)选修2-1第一章“常用逻辑用语”的第一节“命题及其关系”的第一课“四种命题”.本节内容既是初中命题知识的延续，又是高中后续知识的基础.教材以具体命题为例，用特殊到一般的研究思路，从形式结构和内容真假两个方面研究了四种命题及其关系，得出构造四种命题的方法，归纳出互为逆否关系的两命题同真假的结论，为进一步学习充要条件及推理证明奠定基础[1].教学重点是发现和应用互为逆否命题同真假规律.教学难点是如何引导学生发现并了解四种命题及其关系.

2.3 教学目标

(1)通过经历四种命题的构造过程，了解四种命题的概念及其相互关系；(2)通过题组发现互为逆否命题同真假规律并能够判断较复杂命题的真假；(3)体会特殊到一般、正难则反等数学研究方法，发展数学抽象、逻辑推理等核心素养.

3.教学设计

3.1 温情独白，悦纳心灵

师：二十年前追梦考入梁丰，三年高中学习的场景仍历历在目，今有缘重回母校研讨智慧课堂，倍感温馨与亲切.母校悠久的历史和严谨的学风校风深深影响了一代又一代梁丰人的成才成长，……，祝愿学弟学妹们在校训“品端成梁，学粹至丰”的引领下，学习的每一天都是快乐幸福和学有所获的.

设计意图：寻找最合适的话题作为开场白，用最朴实的语言打动学生心灵，以此获得学生的认同和对课堂的期待，从而消除师生间的陌生感.

3.2 问题情境，激发兴趣

问题1 甲、乙、丙、丁四人商量去看电影.甲说：乙去我就去.乙说：丙去我就去.丙说：甲不去我就不去.丁说：乙不去我就不去.最后有人去看电影，有人没去看电影，则去的人不可能是 (填写序号)

①甲 ②甲、乙 ③甲、乙、丙 ④乙、丙、丁

设计意图：通过一个有趣生动的生活话题，牢牢吸引学生眼球，充分调动学习热情.在众生积极思考又表示困惑的最佳契机，教师点拨：围绕“去不去看电影”这个话题，甲乙从正面说，丙丁从反面说，如何清晰其内在的因果逻辑关系，穿插引用章节语中名人名言“要想获得真理和知识，唯有两个武器，那就是清晰的直觉和严格的演绎.——笛卡尔”[2]，在激发学生学习常用逻辑用语内驱力的同时，巧妙渗透了数学文化和历史.

3.3 回顾旧知，激活思维

问题2 你还记得初中是如何定义命题概念的？

练习判断下列语句哪些是命题？

(1)x<2.

(2)如果两个三角形全等，那么它们的面积相等.

(3)若sinα>sinβ，则α>β.

(4)两条平行线的同位角相等.

问题3 你能就学过的数学知识，举出一些命题的例子么？

设计意图：回顾初中命题概念，以旧引新，从而进一步掌握判断命题真假的方法：假命题仅需举出反例即可，真命题则要严格说理.同时，在练习后鼓励学生自主举出命题并交流展示，拓展知识深度和广度.而后，总结归纳命题的一般结构形式(由条件和结论两部分构成)，并将学生例举的命题改写成“若……,则……”、“如果……,那么……”形式”.最后，总结改写的主要目的是使命题的条件和结论更加清晰明确，并且启发学生改写的方式不唯一(选择简洁清晰形式)，多路径发展学生学力.

3.4 建构概念，揭示关系

问题3 针对练习命题(2)“如果两个三角形全等，那么它们面积相等”，你能否围绕“全等”与“面积”两者之间的关系构造出新的命题？

此处让学生集思广益，广泛发言，教师充分鼓励每一个学生表达自己的想法，而后释疑解惑：如果用“若p则q”表示命题，其中p、q分别表示两个语句，非p、非q分别表示p、q的否定，将它们依照(若，则)形式一一排列，则可以得到16个序对：(01)(p,p)；(02)(p，q)；(03)(p，非p)；(04)(p，非q)；(05)(q,p)；(06)(q,q)；(07)(q，非q)；(08)(q，非q)；(09)(非p，p)；(10)(非p,q)；(11)(非p，非p)；(12)(非p，非q)；(13)(非q,p)；(14)(非q,q)；(15)(非q，非p)；(16)(非q，非q).其中，(01)、(06)、(11)、(16)自身至自身不予研究；(03)、(08)、(09)、(14)自身矛盾直接删除.(02)与(04)、(05)与(07)不能两立，只能取一，不妨取(02)和(05)；而(02)与(10)、(05)与(13)不能两立，既取(02)和(05)就舍去(10)和(13).因此仅剩下(p,q)；(q,p)；(非p，非q)；(非q，非p)这四种命题形式.

设计意图：从教材最基本的“如果两个三角形全等，那么它们的面积相等”这一案例出发，让学生尝试发现共有多达16种命题的结构形式，在与学生讨论中不断取舍，总结发现仅有4种命题形式具有研究的价值，从而解决学生对于教材中为何只研究四种命题形式的困惑.

问题4 将原来的命题及同学们给出的三个命题分别编号如下：

如果两个三角形全等，那么它们的面积相等.①

如果两个三角形的面积相等，那么它们全等.②

如果两个三角形不全等，那么它们的面积不相等.③

如果两个三角形的面积不相等，那么它们不全等.④

你能说明命题②与①、命题③和①、命题④和①之间的关系么？

设计意图：基于维果斯基的“最近发展区理论”，着眼于学生的最近发展区，在学生已经明确四种命题基本形式的基础上，超越其最近发展区而自然生成“四种命题”基本概念，并在图1结构基础上进一步完善，最终形成图2网络体系.

图1 图2

3.5 小试牛刀，探究规律

例1 写出下列命题的逆命题、否命题、逆否命题，并判断它们的真假.

(1)若a=0，则ab=0.

(2)若一个四边形的四条边相等，则它是正方形.

(3)若a=b，则2a=2b.

(4)若a>b，则|a|>|b|.

问题5 观察上面的四组例子，探究四种命题的真假之间有什么关系？

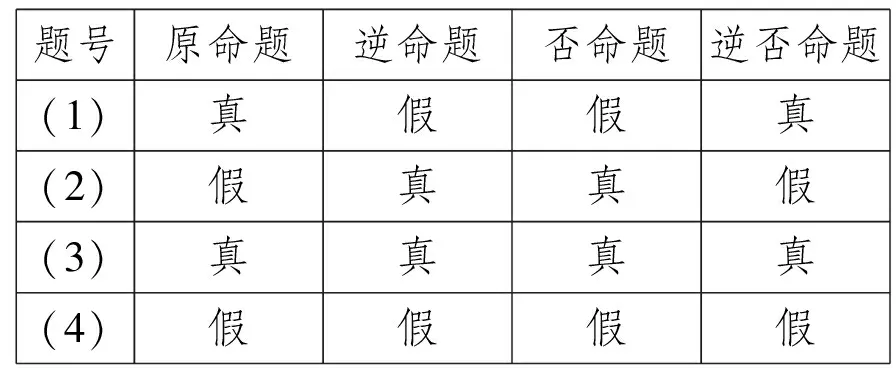
题号原命题逆命题否命题逆否命题(1)真假假真(2)假真真假(3)真真真真(4)假假假假

设计意图：精心设计题组，让学生动手写出命题的四种形式并判断真假，进而发现互为逆否命题同真假的结论(互逆、互否命题的真假没有必然联系)，体会从特殊到一般的数学思想方法.同时指出科学归纳法存在一定的不确定性，必须要有严格的推理证明才能说明结论正确，引发学生课后探究的兴趣.

3.6 数学应用，拓展思维

例2 判断下列命题的真假.

(1)若x2≤0，则x≤0.

(2)已知函数f(x)在(-∞,+∞)上是增函数，a,b∈R，命题“若a+b≥0，则f(a)+f(b)≥f(-a)+f(-b)”的逆命题.

设计意图：通过实例解决为何学习“四种命题”的疑惑，有意识培养学生形成“正难则反”的逆向思维能力.最后，返回思考课堂伊始提出的“去不去看电影”问题，使得课堂的拓展应用起到了前后呼应的效果，让学生有满满的获得感和成就感.

3.7 课堂小结，反思升华

问题6 通过本节课的学习，你能就“为什么要学四种命题”、“四种命题学会了哪些知识和数学方法”分享学习心得么？

设计意图：通过设计这两个问题，帮助学生站在数学知识体系为何发展、如何发展的高度，体会逻辑知识在日常生活和数学学科中的价值.

3.8 课后延伸，发展学力

1.自己写一个数学命题，写出它的逆命题、否命题与逆否命题，并判断它们的真假.

2.上网查阅资料，并尝试用集合知识证明：互为逆否关系的两个命题同真假.

设计意图：分层设置不同习题，学生可根据自身情况自主选择一二，满足不同学生巩固和发展学力的需要.

4 感悟与思考

4.1 发现教学智慧

《教育大辞典》中将教学智慧定义为：“教师面临复杂教学情境所表现的一种敏感、迅速、准确的判断能力.”由于是借班上课，在设计本节课的时候，笔者一直考虑以如何的方式激发学生学习的热情，最快形成相互间的一种默契.在课前走进教室的一霎那间，猛然发现自己认识梁丰正好二十年，于是就有了娓娓道来的一段独白，赢得了学生的热烈掌声，从而达到良好的开端等于成功一半的效果.

教学智慧，不仅体现在追求课堂效率，更是追求的一种境界，要让学生学得快、学得好的同时，更要学得轻松、学得愉快，最终学得自由、学得开放.四种命题及其关系的概念教学是本节课的难点，对于概念的引入，在让学生充分思考的基础上，或小组讨论，或师生互动，通过观察、分析与比较，在形成16种命题结构形式的基础上发现仅有4种具有研究价值的命题形式，既解决了四种命题及其之间的关系，更重要的是解释了学生对于教材中为何只研究四种命题形式的困惑.又如发现和自觉应用互为逆否命题同真假规律是本节课的重点，在教学设计时，通过精心设计题组，从原命题和逆命题的真假全覆盖着手，既有利于学生发现规律，也不至于让学生产生误解.

4.2 发展学生学力

李庾南老师在文献[3]中指出，学生学力主要指学生借助一定的教育环境和能力及积极的教育实践活动，所形成的自我获取、自我建构、自我发展、自我超越的态度、知识和能力的总和.学力是教育情境下学生学习效果和教师教育质量的重要体现，更是人持续发展的表征.在本节课的教学设计中，研究从16种命题结构形式一步步通过分析、思辨，最终精简到只需研究4种命题形式的过程，不仅让学生明白知识的发生、发展以及溯源等过程，也使得学生获得了自主创造、自我超越的成功体验.更高层面上，学生就掌握了解决问题的一般方法与途径，悟出了基本的学习之道.

与此同时，发展学生学力更需要发展教师学力，要从指向应试向旨在培养学生的学习动机与主动应对社会变化的能力的转变.本节课中，通过多次设置“你能再举出一些命题”、“如何构造新的命题”等开放度较高的问题串，再加以在交流互动中教师语言的风趣幽默、激情飞扬，促使学生始终保持愉悦的心情、强烈的求知欲、积极的思维探究、友好的合作态度，达到各自的最近发展区，自主获取和灵敏建构知识体系，形成利用数学的眼光观察世界、数学的思维分析世界、数学的语言表达世界的能力.

4.3 互联网+教学

当下，互联网+大数据在各个行业得到了蓬勃发展，本节课，借助白板、实物投影等多媒体技术，一定程度上呈现了知识的生成、发展和应用过程，但笔者对具体某一个学生掌握的情况如何心里还是一个未知数.况且在日常的教育教学活动中，大多数教师依旧是一支粉笔、一块黑板行天下，课堂互动基本还是停留在师生一对一、点对点的低效模式，距离精准教学还有很长一段距离.十九大报告中，习总书记提出要继续深化教育改革，加快教育现代化及网络教育.随着智能教育的迅猛发展以及技术支撑的日益完善，当练习测试可以同步上传网络、自动批改、错题举一反三、生成评价报告的时候，当每一个学生的课堂思维可以通过数据即时呈现并能跟踪记录个性学习的时候，就更需要教师聚力教育智慧，基于学生已有经验、问题等不断优化教学设计，着力关注数学的学科价值，着重培养学生成为现代社会公民所必备的核心素养，从而不断促进学生的学力发展.