指数函数定义中“规定”的成因探究
2018-07-30上海市嘉定区第二中学201800牟忠智刘国平
上海市嘉定区第二中学 (201800) 牟忠智 刘国平
一、教学片断
指数函数是高中阶段继幂函数后研究的第二个具体函数.指数函数概念教学常常被用来开设展示课,观摩教学中发现,教师对指数函数定义中底a的规定原因的解释差强人意.
案例1:“指数函数概念”教学片断.
引入:
问题1 某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……,一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x之间构成一个函数关系,能写出x与y之间的函数关系式吗?
学生:y与x之间的关系式,可以表示为y=2x.
问题2 一种放射性物质不断衰变为其他物质,每经过一年剩留的质量约是原来的84%.设最初的质量为1,时间变量用x表示,剩留量用y表示.求出这种物质的剩留量随时间(单位:年)变化的函数关系.
学生:y与x之间的关系式,可以表示为y=0.84x.
概念形成:
指数函数的定义:一般地,函数y=ax(a>0,a≠1)叫做指数函数,其中x是自变量,函数的定义域是R.
对规定“a>0,a≠1”的讨论:
师:指数函数定义中,为什么规定a>0,a≠1?
学生分组讨论,开始时比较茫然.教师提示:如果不这样规定会出现什么情况?老师将问题分解为:
(1)若a<0时会有什么问题?
(2)若a=0会有什么问题?
(3)若a=1又会怎么样?
学生似有所悟,各组大都得出以下结论:
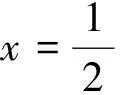
(2)若a=0时,对于x≤0,ax无意义,对于a>0,函数值都是0,没有研究的必要.
(3)若a=1时,1x无论x取何值,它总是1,太简单,没有研究的必要.
师:为了避免上述各种情况的发生,所以规定a>0,a≠1.
……
二、案例分析
案例1中,教师对指数函数定义中“a>0,a≠1”的规定的解释具有普遍性,绝大多数老师在授课中都是这样解释的.
高级中学课本数学高一年级第一学期(试用本)[1]教材引出指数函数定义后,在相关内容的旁白处,以问题的形式提出:为什么规定a>0,a≠1?
教学参考书上给出的理由和例题1中教师给出的理由相同.
这样的解释科学吗?我们可以通过案例2进行说明.
案例2 函数y=(-2)x的研究.
考虑特殊情形,an=(-2)n,n∈N*.
这是一个以-2为首项,-2为公比的等比数列,也可以看成是以-2为底,定义域为N*的指数型函数.
说明如果定义域为N*,就不需要规定a>0,a≠1.
更一般的,我们研究关系y=(-2)x.
在x的允许值的范围内,对每一个确定的x,y=(-2)x的值唯一确定.因此,它是一个函数.它具有以下性质.

图像:在x的允许值的范围内,适当的选取x,通过描点法,可以画出函数y=(-2)x的图形如下:
图像是不连续曲线.图像恒过点(0,1).
定义域:使y=(-2)x式子有意义的x的取值集合,无法用确定的集合表示.但定义域不是R.
值域:实数集的一个真子集,无法确切表示.
奇偶性:非奇非偶.
单调性:函数不具有单调性.……
由此可见,即使a<0,关系y=ax也是函数,且这个函数的定义域不是R.
换而言之,指数函数定义中底“a>0,a≠1”的规定是因为“必须满足指数函数定义域是R”才产生的.
众所周知,中学阶段涉及到的函数,如一次函数,二次函数,反比例函数,幂函数等等,大多是先有解析式而后有定义域.定义域是由解析式来决定的,一般是指解析式有意义时自变量的范围.
那么,指数函数定义中,为什么要先规定其定义域是R呢?
其实,这是由数学规定必须要遵守的规律决定的.

三、数学规定遵循的原则
1.方便性原则:方便性原则是指定义概念时要考虑到使用和研究的方便,它包括读、写、记忆、计算及推理的方便.
数学上的规定必需有利于数学的研究,有利于数学的创造.记a×a×a×…×a×a(1000个)=a1000,规定后的乘方运算要比原来的乘法式子简单多了;阿拉伯数字及其运算法则在全世界通用,但是罗马数字及其运算规律没有普及,原因也是基于阿拉伯数字及其运算方式的方便性.
2.合理性原则:一个概念的正确定义,除了反映事物的本质属性外,还要具有合理性.
案例3 规定a0=1(a≠0)的原因.
指数概念的发展初期,am(a≠0)表示m个a相乘;随着指数m变化,如m是零、负数、分数、无理数时,am(a≠0)就不能看作是m个a相乘.
考察运算法则:am÷an=am-n(a≠0),当m,n为正整数且m>n时,结果完全符合初期“am(a≠0)表示m个a相乘”规定的意义.
但是当m=n,或m 运算法则的需要和指数初期规定的矛盾要求将指数的概念加以推广.. 怎样拓展指数的概念比较合理? 以a0为例,当m=n时,运算法则am÷an=am-n=a0(a≠0), 等式左边的值为1,如果要是运算法则成立,就必须有a0=1(a≠0). 所以规定:a0=1(a≠0). 这样的规定遵守一条原则:原有的指数概念及运算法则必须适合推广后的指数概念及运算法则,这就是合理性原则. 3.简明性原则:简明性就是简洁性,在概念的正确定义、准确完备的前提下,力求简洁,简单. 案例4 反正弦函数的定义 为什么这样规定? 其实这样规定的主要原因是“简单”,可以看成是优选出来的结果.数学运算中常设某量为1而不是设它为8.2753是同样的道理. 除此之外,数学规定还必须满足确定性原则、启发性原则、和谐性原则等原则,其中和谐性原则是指定义之间的和谐性,体现的是数学的和谐美. 现在再来研究指数函数定义中“规定”的成因. 案例2说明,当a<0,关系y=ax也是函数.这个函数的定义域不是R. 这个函数的定义域、值域无法确切表示;函数也不具有奇偶性和单调性;函数的图像无法确切画出…….在这样的条件下,函数图像及性质都很复杂,在中学阶段无法研究. 所以,关于指数函数底的规定的理由是为了方便研究.主要是为了遵循“规定”的方便性原则. 综上所述,我们可以这样理解指数函数中规定底a>0且a≠1的理由: 指数函数中规定底a>0且a≠1是为了满足定义域为R的规定,规定定义域为R是为了研究的方便. 教学中如果这样对学生解释,应该是客观的,合理的.如果有同学对这样的规定提出质疑,同时进行更深入的研究,那就是数学的福音了. 数学中还有许多这样的规定或概念,教学过程中有些教师的解释似是而非,如二面角的平面角的定义等.从某种角度来看,对数学规定的来由探究并不是教学的内容,但是只有理解了为什么这样“规定数学”,才能做到我也能“规定数学”,如果我们学生中有部分能够做到有能力“规定数学”,那就是数学教育的最高境界.
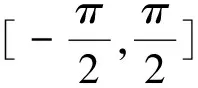
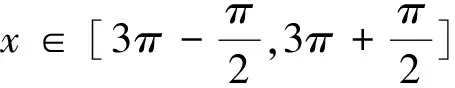
四、结论
