小学生数学隐性学力的提升
2021-05-20梁华重
梁华重
(广西靖西市吞盘乡孟麻小学 广西 靖西 533813)
前言
目前,随着教育教学水平的持续化提升,小学数学教学的质量也在持续地提高。但在实际的教育教学工作实施和开展中,重视学生的显性学力的开发与提升,关于学生的隐性学力的建设和发展依然停留在原地。传统的固化教学思维,无法从根源上为学生提升隐性学力提供环境和机遇。很多教师还存在对学生隐性学力认知不清,捉摸不透的现象,基于此,下文将对隐性学力与显性学力差异进行区分,进一步探究和分析如何提升小学生数学隐性学力。
1.隐性学力与显性学力之间的区别
显性学力与隐性学力两者之间是相互区别,又彼此联系的关系。首先,显性学力是比较容易被发现和觉察的,是一种表现在外的学习结果。而隐性学力是比较不容易被发现和觉察的,是一种表现在内的学习结果。其次,显性学力通常只局限在学生的认知层面,是认知上的学习成果,而隐性学力则除了包含上述的认知学习结果,还包含学生的学习兴趣、态度、价值观导向等内容的成果。再次,认知结果层面上看,显性学力则更多指向学生的知识储备以及技能提升的结果,而隐性学力则是代表学生的学习方式、方法以及思维形成的成果。此外,隐性学力更倾向于学生的“学习潜在能力”的开发,其更强调对学生日后成长发展的作用,而作为显性学力则代表的眼下学生能力和成果以及表现。隐性学力比显性学力更根本、更重要[1]。
2.小学数学教师如何提升小学生的隐性学力
2.1 使隐性学力促进显性能力的提升。在日常教学过程中,作为教师大多是关注学生的显性学力培养,而忽视了学生隐性学力提高。而事实上,隐性学力与显性学力相比较,则更为重要。显性学力的提高能帮助小学生更好的掌握具有难度的更为抽象的数学知识,提升对数学学习的热情,往往在日后的学习中能发展出更大的学习潜力。
例如:“加法运算律”这一单元的教学中,可对加法交换律开展如下的教学方式。
教师:通过板书上的两道算式15+37=52 37+15=52,同学们,你们发现了什么?
学生:两组算式的计算结果相同。
教师:同学们,你们是否能用一个算式符号将两组算式连接起来呢?
学生:可以,15+37=37+15。
教师:请同学们来观察等式两边,能发现他们之间有什么联系吗?
学生:交换两个加数的位置,和不变。
(教师板书后,面带微笑等着学生继续回答)
学生:我觉得不一定所有算式都适用啊?这样下定论,是不是太心急了?
教师:那怎么样才能下准确的定义呢?
学生:应该通过更多的实例来验证这个定论。
学生:老师,我们还能找到其他反例来推翻刚刚的定论。
通过上述的案例,我们可以看到“交换两个加数的位置,和不变”是学生容易出现困惑的教学难点。若教师只是单一的叙述概念和定义法则不会从根源上提升学生的学习兴趣,还会导致学生难以理解和消化,在日后做题中也容易出错。而若采用巧妙的体态语言,给学生留足思考和分析的时间,通过一正一反的验证方式对规律加以验证,则会起到良好的教学效果[2]。
2.2 习题设计,关注小学生数学探究的过程。曾经有教育学者这样说:“学习应成为意义创造过程之中的探险。”而就当下我国的小学生探究能力与其他欧美的发达国家相比,还存在很大的差异。基于此,作为一名小学数学教师,应给予学生更多探究分析问题的思考时间,不要以标准化的思维禁锢学生的发展。通过生动有趣的习题设计,将数学的学习思维简单化、具体化、趣味化,以便更好的激发学生的研究能力,通过习题活动的参与,获取知识层面更为丰富的新知识。
例如:我们在讲解“圆柱的表面积和体积”这一课题时,对“已知圆柱形容器的底面半径或直径和高,求容器至少需要多少铁皮和它的容积”这种题目是学生做练习题时常见的内容[3]。若对圆柱表面积和体积公式进行反复多次的机械训练,只能让学生反复套用公式,其与学生的生活实际生活联系不够紧密,无法调动学生的主观能动性,对学生的探究能力形成与培养十分不利。为了改变这一现状,提升学生的热情和兴趣,我们可以开展以下的习题设计。
首先,教师可以收集身边的废旧材料,出示下面的例题:
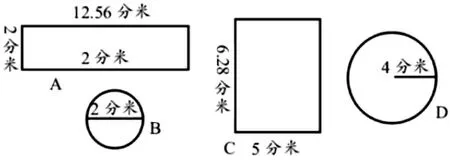
题目1.废旧材料组合
小明想用这些材料,制作一个没有盖子的圆柱形铁皮桶,同学们,觉得应该用A、B、C、D、中,哪两种材料作为合适呢?
题目2.素材信息重组
通过选定的题目完成铁皮桶的制作,该水桶的容积是( );张师傅若拿来另一个35平方分米铁皮与同学们做的铁皮桶进行交换,那么,张师傅所带来的材料损耗是( )。
题目3.探索与创新
若我们选择铁皮A,那我们所制作的铁皮桶底面积是多少呢?容积发生改变了吗?若改变容积是( )。
结语
近些年,伴随小学数学教学研究的深入,学生隐性学力培养,已经备受教育工作者的关注,作为一名小学数学教学的一线工作者,只有区分隐性学力和显性学力,使隐性学力促进显性能力的提升,通过习题设计,关注小学生数学探究的过程,才能采取更多更有针对性的措施,提升对学生隐性学力的提升,以隐性学力回归显性学力,促进学生未来数学学习能力的提升与发展。
