液压配气机构凸轮柱塞接触应力研究

(贵阳市花溪区工业和信息化局，贵州 贵阳 550025)

0 引言

凸轮传动是机械传动中应用广泛的一种传动方式。尤其是在自动机械中，凸轮机构扮演着重要的角色。通过对凸轮型线的设计能够使凸轮从动件完成我们所需要的运动，现在凸轮机构都向着高精度、高速度、高可靠性、高传动效率和高承载能力发展[3]。在汽车发动机的配气机构中，凸轮在高速高承载工况下的受力及运动特性是设计凸轮的一个重要的考虑因素，随着液压配气机构的发展，很多液压配气系统也广泛采用凸轮机构。在这种凸轮机构中，主要是通过凸轮推动从动件来改变液体的容积，从而产生液压力来驱动气门运动。由于凸轮从动件受到液压波动力的影响，使得凸轮与从动件的接触受力十分复杂，因此，研究这种凸轮系统的动力学特性就显得十分必要。本文分析了一种新型液压配气机构的凸轮柱塞的受力及运动特点，该凸轮柱塞由两段结构组成，柱塞小头主要用于导向，大头主要承受柱塞缸侧向压力。根据设计参数、凸轮型线函数和该凸轮系统的特点建立了液压柱塞从动件的动力学方程，计算并校核了凸轮与滚子的接触应力。

1 动力学方程的建立与求解

符号说明：Fn凸轮对滚子的法向力；Fn1柱塞缸壁下端对柱塞的正压力；Ff1柱塞缸下端对柱塞的摩擦力；Fn2柱塞缸对柱塞小头的正压力；Ff2柱塞缸对柱塞小头的摩擦力；Fk弹簧对柱塞的弹簧力；α凸轮压力角；y是柱塞从动件的位移，向上表示凸轮处于推程段。

图1 凸轮柱塞从动件的受力分析示意图

设计计算的各参数名称及其设计值如表1。

表1 设计参数表

根据发动机配气要求以及液压的特点设计的柱塞从动件在凸轮推程段的位移方程为：

(1)

由于相比液压力来说弹簧力很小，所以忽略弹簧力Fk，根据图1及给定的各参数可建立下面的动力学方程：

铅垂方向平衡方程为：

Fn*cos∂-Ff1-Ff2-Fp=m*y″

(2)

水平方向平衡方程为：

Fn*sin∂-Fn1+Fn2=0

(3)

以滚子中心O2为简化点的力矩平衡方程为：

Ff1*R2+Fn2*(H2+L1-β1*L1-y-rb-r0)-Ff2*R1-Fn1*(H1+β2*L2-rb-r0-y)=

(4)

由图1可知，柱塞小头的配合长度为：

L1=y+r0+rb+L20-H2

(5)

代入各设计参数得：

L1=y+6.7

(6)

其中：0≤L1≤L0=7.5

柱塞大头的配合长度为：

L2=y+r0+rb+L10-H1

代入各参数得：

L2=y+7.6

(7)

凸轮推动柱塞在高速运动时，柱塞腔里的液压压力波动是很复杂的，使得液压作用在柱塞上的液压力很复杂，为了简化计算，根据柱塞的位移对应的柱塞腔内的最大最小压力值通过线性插值可以求得液压力。

由线性插值得压力与柱塞位移的关系为：

(8)

所以液压对柱塞上部产生的液压力为：

Fp=P*S

=120.6y+301.4

(9)

根据以上式(2)到式(9)的动力学方程联合求解以及凸轮推程段的柱塞从动件位移函数(1)式可以计算出柱塞所受的法向力Fn和两个侧向力Fn1和Fn2，本文根据发动机的工作特点计算了凸轮在n=400 r/min、n=1500 r/min和n=3000 r/min这三个转速下凸轮柱塞所受的法向力Fn和两个侧向正压力Fn1和Fn2。

由图2、3、4可知，在不同的转速下，柱塞所受的三个力的变化趋势基本一致，在凸轮的推程阶段凸轮与柱塞滚子的法向力Fn都逐渐的增大，当液压腔的压力达到一定值后法向力的增幅越来越大，当液压的压力足以打开发动机气门之后这个力就按照一定的规律增大。而侧向力Fn1先是逐渐增大，达到一个最大值之后又慢慢减小，并且不同的转速下达到最大值时的凸轮转角都不一样，对比三个图可知，随着转速的增大，Fn1达到最大值趋于提前。侧向力Fn2先增大后减小，在凸轮转角约为28.5°的时候变为负值，而且在不同的凸轮转速下的变化点基本一致，即在这一点上侧向力Fn2发生了方向的改变，其方向变为与Fn1同向，通过这个换向使得柱塞的单面受力变好，由于柱塞与液压腔壁的接触面增大，这样就减小了柱塞在运动过程中发生胶合的可能性。通过计算得知，在增加柱塞腔的导向长度以后，Fn2从凸轮转角为零开始就与Fn1同向，这样在整个凸轮的推程中柱塞的受力都处于一侧接触受力状况，这种受力特点减小了柱塞与柱塞缸运动配合面发生胶合的可能性，有效改善柱塞工作的可靠性。由此可知，可以通过优化凸轮及柱塞缸导向长度来提高系统的动力学特性，从而提高系统的可靠性和稳定性。

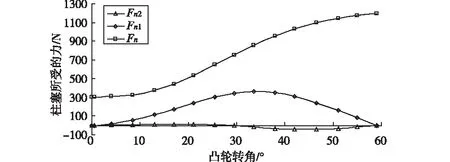
图2 n=400 r/mm时凸轮柱塞的受力计算图

另外，通过对比图2、3、4可知，随着凸轮转速的增大，凸轮对柱塞的法向力Fn的增长规律不同，在n=400 r/min和n=1500 r/min时的法向力的最大值均在凸轮推程最大转角59°处达到，分别为1196 N和1103 N。而在n=3000 r/min时的法向力Fn的最大值在凸轮转角约为20.5°处达到，其值约为833.7 N。对比这三个最大值可以发现，随着凸轮转速的增大，凸轮与滚子的法向力Fn的最大值逐渐减小，这主要是由于在高速时柱塞的惯性力很大导致的。

图3 n=1500 r/mm时凸轮柱塞的受力计算图

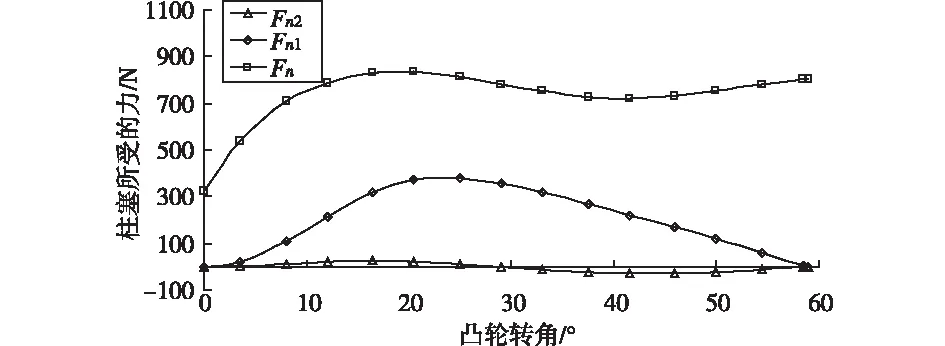
图4 n=3000 r/mm时凸轮柱塞的受力计算图

2 凸轮与滚子的接触应力计算

在各种凸轮机构中，凸轮及其从动件的接触应力满足工作要求是保证该机构正常工作的前提，对于高速和承载较高的凸轮系统，系统在工作的过程中更容易发生强度不足的故障。因此，接触应力的校核计算尤为重要，接触应力的计算能够引导我们去选择各构件的材料以及进行系统结构尺寸的优化设计。一般凸轮的运动很简单，但是由于凸轮型线的复杂多样就使得凸轮从动件的运动十分的复杂，凸轮在每一个转角处的曲率半径都不一样，压力角也不一样，每一个接触点的接触法向力都不一样。对于本文的系统来说，由于与凸轮接触的柱塞受到液压力的作用，而柱塞腔内的液压压力波动很大，这就使得凸轮与柱塞的法向力Fn变化很复杂，且该系统是在很高转速下工作，因此在系统动力学分析中，计算凸轮的接触应力是否满足要求就显得十分必要。

2.1 凸轮曲率半径的计算

参考机械设计手册[6]，凸轮理论轮廓曲率半径公式为：

(10)

由于本文中e=0，所以上式变为：

(11)

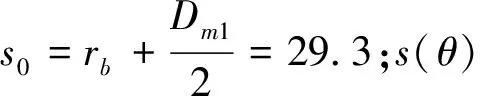
代入从动件初始位移(11)式变为：

(12)

令ρ为综合曲率半径，则：

(13)

代入滚子的直径计算综合曲率为：

(14)

由式(12)和(14)以及凸轮推程段型线函数(1)可以计算综合曲率随凸轮的推程转角变化如图5。

图5 凸轮推程段综合曲率图

由图5可知，随着凸轮推程角的增大，综合曲率总体趋势是逐渐增大的。在凸轮推程角约为10°时略微开始有所减小，到凸轮转角约为17°时又开始增大。这主要是凸轮在推程段有一段与滚子形成内接触的原故。综合曲率在推程角最大处取得最大值0.211，这与凸轮推程型线方程(1)加工出来的凸轮结构特点是相吻合的。

2.2 接触应力的计算

根据赫兹接触应力理论可知接触应力计算公式为[2]：

(15)

式中：Fn两个接触面的法向力N；b两个接触体的宽度mm；E1、E2两个接触体材料的弹性模量MPa；μ1、μ2两个接触体材料的泊松比；ρ1、ρ2两个接触处的曲率半径mm，+、-分别用于外接触和内接触。

根据使用材料查得：

E1=E2=206 GPa，μ1=μ2=0.3

代入各参数计算(15)式：

(16)

由式(15)可知，接触应力不仅与所选材料的性能以及相互接触的结构特点有关，还与二者之间的法向力有关。根据前面对凸轮在不同的转速下时柱塞所受的法向力Fn计算分析可知，法向力Fn在凸轮低转速时取得最大。由式(16)可知当法向力最大时，接触应力也达到最大值。因此，根据发动机的工作特点，在怠速时转速最小，此时凸轮转速约为n=400 r/min。因此选取凸轮转速n=400 r/min时来计算凸轮与柱塞的接触应力，如果计算的接触应力能够满足设计要求，那么凸轮在其他转速下就能满足接触应力的设计要求，凸轮转速n=400 r/min时，凸轮在推程段的接触应力的计算结果如图6。

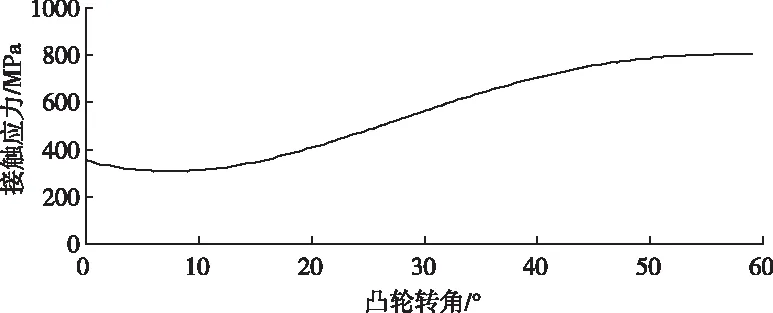
图6 n=400 r/min时凸轮与柱塞的接触应力图

由图6可知，凸轮与柱塞的接触应力的最大值发生在从动件的位移最大的时刻，这个时刻也是发动机气门开启最大的时刻。从图上可看出，此时的最大接触应力为807.776 MPa，对于这个接触应力选择一般的工具钢就能达到要求，工具钢在润滑良好的条件下许用接触应力可以达到1336 MPa[1，2]。所以在进行凸轮系统的结构优化的时候适当减小凸轮系统结构尺寸使得系统的空间结构紧凑而使接触应力增大在有限的范围内也是可以满足设计要求的。

3 结论

建立凸轮及柱塞从动件的物理模型和数学模型，分析了从动件在运动过程中的受力情况，建立了从动件的动力学方程，并根据设计尺寸计算了从动件的受力大小及其变化规律，由计算的结果得出如下结论：

1)根据侧向正压力换向的特点，为了减小柱塞与柱塞缸壁发生胶合的可能性，一方面可以加长柱塞导向的长度来改善柱塞与柱塞套的接触受力状况，从而增加系统的可靠性和稳定性。另一方面可以选择锡青铜等耐磨且抗胶合能力较好的材料。

2)由于受到惯性力和压力波动的影响，法向力Fn的最大值随着凸轮转速的增大反而减小，通过对凸轮与柱塞滚子的接触应力的计算，发现二者之间的接触应力不是很高，选择一般的工具钢就能满足设计要求，而且在钢对钢的许用接触应力的范围内还可以减小系统的结构尺寸，使系统的空间结构更加紧凑。