基于ANSYS的船舶凸轮机构瞬态动力学分析

孟文静

(安徽粮食工程职业学院 机电工程系,安徽 合肥 230000)

凸轮机构是机械装置中常见的机构,在自动化器械中尤为常见[1]。凸轮一般作为主动件做等速转动,但也有做往复摆动或移动的。被凸轮直接作用的构件叫作推杆,又被称为凸轮从动件,若凸轮作为从动件则称该结构为反凸轮机构[2]。推杆的行程、速度及其加速度决定了凸轮的轮廓曲线,因此推杆的运动规律对凸轮机构的设计起着至关重要的作用[3]。凸轮从动件对于凸轮机构来说是不可或缺的,它的运动规律直接决定它所在机械装置的性能以及工作特点,故凸轮从动件的运动规律对凸轮轮廓曲线的形状也起着决定性的作用[4]。凸轮从动件的运动规律其实就是凸轮转角变化时从动件速度、加速度和位移等的变化规律。根据运动规律数学表达式的不同,可以把从动件运动规律分为三角函数运动规律与多项式运动规律[5]。多项式运动规律主要适用于中低速轻载的工作环境,这是因为多项式运动规律虽存在着较为明显的冲击,但制造过程简单,价格便宜,所以一般用在要求不太高的机械设备上[6]。三角函数运动规律适用于中速、中载并且不存在明显冲击的凸轮机构,但这种凸轮机构的制造过程比较复杂且成本较高,一般用于要求较高的机械设备[7]。在凸轮机构设计中,ANSYS是应用较为广泛的建模软件,它能准确地建立模型并分析凸轮机构运动情况。目前,基于ANSYS软件对凸轮机构的研究很多,包括建模设计、结构优化、运动规律分析等[8-9],然而对于凸轮机构从动件的研究较少,缺乏典型凸轮机构从动件变形与未变形的模型及其应力分布、运动规律的研究。本研究基于ANSYS软件对船舶凸轮机构进行建模,将预先设计的载荷加载到模型关键点上并进行求解,分析从动件位移与速度、加速度的关系,并构建结构失稳变形图,计算其形变位移和应力分布。

1 相关理论概述

1.1 瞬态动力学分析

瞬态动力学分析的主要特点是它可以用来分析载荷随时间不断变化时结构的应力、应变及其位移等。瞬态动力学分析的基本运动方程[10]为

(1)

1.2 凸轮的基本概况

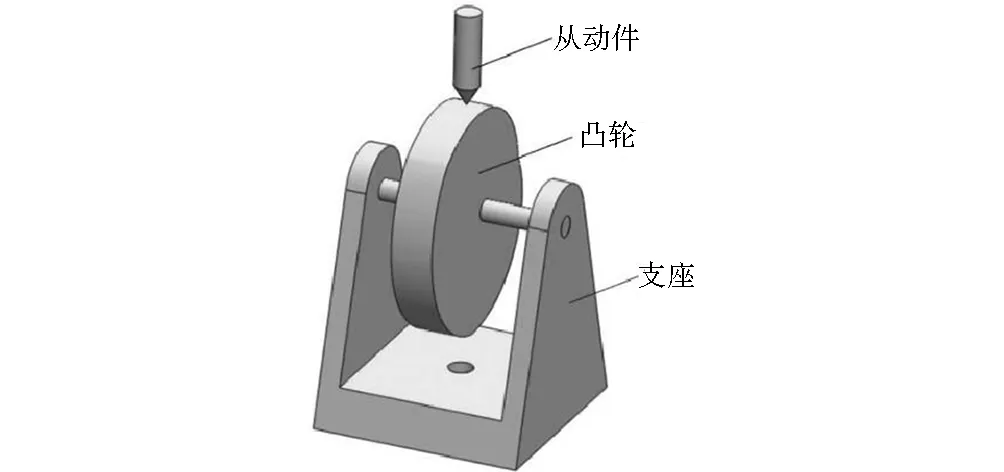
图1 凸轮的基本结构Fig.1 Basic structure of cam

1.2.1位移运动规律曲线

利用多项式设计凸轮从动件位移运动规律曲线[11]:

s(θ)=c0+c1θ+c2θ2+…+cnθn,

(2)

θ=ωt,

(3)

式(2)和式(3)中:θ为凸轮的转角,(°);ω为凸轮的转速,r/s;t为凸轮转动时间,s。凸轮运动过程中,从动件沿着凸轮外侧运动,运动过程主要分为近休止、升程、远休止、回程。

1.2.2加速度运行曲线

凸轮从动件系统在传递运动的同时给激励对象施加激励,为了解凸轮从动件的激励特性,把从动件的加速度曲线展开成傅里叶级数,该曲线可表示为

(4)

式中:a0、ai、bi为傅里叶系数。

1.3 凸轮从动件的建模

基于ANSYS软件对凸轮从动件进行建模,生成位移速度图、位移加速度图、等高线应力云图和结构失稳变形图,并将分析得出的结果与预期进行对比,判断其是否符合要求。

1.3.1定义材料模型

凸轮从动件材料采用45#钢,其碳质量分数为0.42%～0.50%,材料性能参数如表1所示。根据表1中材料的性能参数在ANSYS软件中定义材料模型。

表1 凸轮从动件材料的性能参数Tab.1 Performance parameters of CAM follower material

1.3.2创建生成回转体

首先创建关键点,NPT1文本的坐标为(0,0,0),NPT2文本的坐标为(0.015,0.015,0),NPT3文本的坐标为(0.015,0.1,0),NPT4文本的坐标为(0,0.1,0),然后依次拾取关键点1和2、2和3、3和4、4和1,创建4条直线并构成面。通过Mesh Tool模块在Mesh区域将单元类型选择为“Quad”(四边形),将划分单元的方法选择为“Mapped”(映射),从而生成回转体,如图2所示。

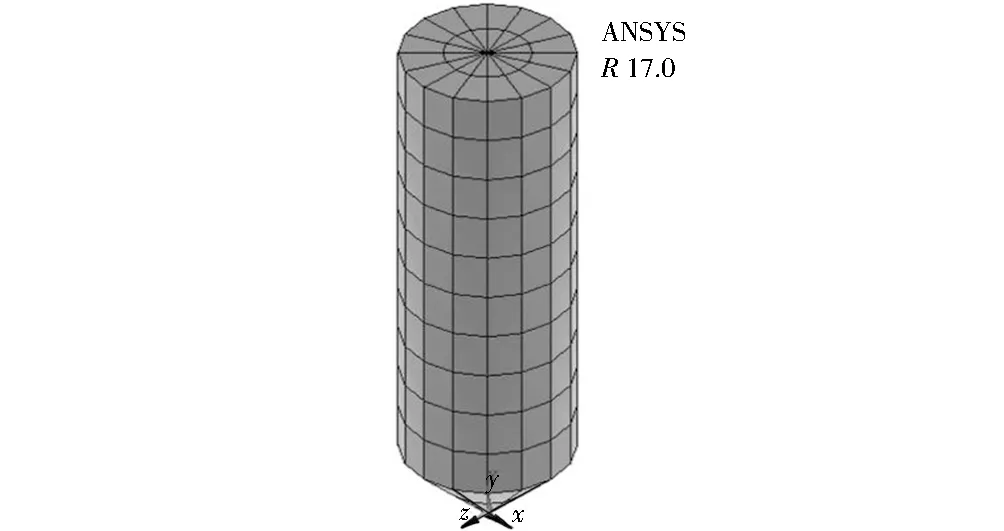
图2 凸轮从动件回转体效果图Fig.2 Effect diagram of cam follower swivel

1.3.3施加约束和载荷

在x、y方向施加约束,即施加在推杆上的径向约束与切向约束,结果见图3。

图3 凸轮从动件施加约束效果图Fig.3 Effect diagram of cam follower restraint

2 结果与分析

2.1 位移与速度对比曲线

图4为位移与速度对比曲线。从图4可以看出:0～10 s时,从动件做匀速运动;10～20 s时,从动件处于停滞阶段,并且在10 s时速度发生突变;20～35 s时,从动件做反向匀速运动,并且在20 s时速度发生突变,此时会产生轻微振动;35～45 s时,从动件处于停滞阶段,并且在35 s时速度同样发生突变。由此可知,在10 s、20 s和35 s时机构会发生轻微压力变化。

图4 位移与速度对比曲线Fig.4 Contrast curve of displacement and velocity

2.2 位移与加速度对比曲线

图5为位移与加速度对比曲线。由图5可知,在10 s、20 s与35 s时加速度趋于无穷大,会产生一定的冲击,其余时间处于匀速状态,运动规律与正弦进行组合,可以减少冲击。

图5 位移与加速度对比曲线Fig.5 Contrast curve of displacement and acceleration

2.3 失稳变形与应力分布

图6为从动件变形结果。从图6可以看出,变形量为2.07×10-4mm,变形量较小,对结构的使用没有影响,满足变形要求(小于工况经验值4.00×10-4mm)。

图6 从动件变形结果Fig.6 Follower deformation results

图7为从动件的应力云图。从图7可以看出,从动件的应力分布是从中心向外逐渐减少的,并且最大应力在从动件尖顶处(13.4 MPa),远小于所选材料的屈服强度(355 MPa),故所选材料合格。如想改善尖顶处的应力,可以将从动件改为滚子推杆,但由于要考虑成本,所以依然使用如图2和图3所示的从动件。

图7 从动件应力云图Fig.7 Follower stress nephogram

3 结语

本研究使用ANSYS软件构建船舶凸轮机构模型并进行了有限元分析,生成变形与未变形的模型边界和应力分布,探讨了位移与速度、加速度的关系。根据ANSYS软件的分析结果可知,凸轮从动件在预期条件下的最大变形量为2.07×10-4mm,变形量很小,在合理的范围(小于工况经验值4.00×10-4mm)内。从动件的应力分布是从中心向外围逐渐减少的,并且最大应力为13.4 MPa,远小于材料的极限值,因此所选材料既符合变形要求又符合材料应力要求,可以满足凸轮机构的使用要求。