A multi-aircraft conflict detection and resolution method for 4-dimensional trajectory-based operation

Siqi HAO,Shaowu CHENG,Yaping ZHANG

School of Transportation Science and Technology,Harbin Institute of Technology,Harbin 150090,China

KEYWORDS Air traffic control;Collision avoidance;Conflict detection;Conflict resolution;Time geography;Trajectory planning

Abstract Conflict Detection and Resolution(CD&R)is the key to ensure aviation safety based on Trajectory Prediction(TP).Uncertainties that affect aircraft motions cause difficulty in an accurate prediction of the trajectory,especially in the context of four-dimensional(4D)Trajectory-Based Operation(4DTBO),which brings the uncertainty of pilot intent.This study draws on the idea of time geography,and turns the research focus of CD&R from TP to an analysis of the aircraft reachable space constrained by 4D waypoint constraints.The concepts of space–time reachability of aircraft and space–time potential conflict space are proposed.A novel pre-CD&R scheme for multiple aircraft is established.A key advantage of the scheme is that the uncertainty of pilot intent is accounted for via a Space-Time Prism(STP)for aircraft.Conflict detection is performed by verifying whether the STPs of aircraft intersect or not,and conflict resolution is performed by planning a conflict-free space–time trajectory avoiding intersection.Numerical examples are presented to validate the efficiency of the proposed scheme.

1.Introduction

For a long time,the description and definition of aircraft trajectory have been three-Dimensional(3D).The importance of time dimension has been explored in recent decades.In the 1980s,the United States Federal Aviation Administration proposed the concept of a National Airspace System to address the rapid growth of air traffic,in which the idea of four-Dimensional(4D)navigation and guidance of aircraft was proposed.The concept of 4D Trajectory-Based Operation(4DTBO)has gradually become a reality with the development of navigation and communication techniques.14D trajectory refers to a sequence of waypoints that consist of 3D coordinates and reliable and reachable timestamps at which a flight reaches these points.In the context of 4DTBO,an aircraft can be controlled by arranging the specific time(Controlled/ConstrainedTimeofArrival,CTA)ofasequenceof waypoints.

Conventional Conflict Detection and Resolution(CD&R)is based on aircraft rather than trajectory.The process of CD&R follows the steps of Trajectory Prediction(TP)-conflict detection-conflict resolution.2Geometric deterministic algorithm3,4has been the mainstream at the beginning of the CD&R study.specifically,during a flight,an air traffic controller needs to monitor the flow of the sector and the location ofthe aircraft.Firstly,a predicted trajectory is generated using a deterministic TP method according to the position,current state,and flight plan of the aircraft.Then,the air traffic control center determines the conflict by comparing the distance between the aircraft and the safety separation criterion based on the predicted trajectory.The air traffic controller needs to conduct interventions on the aircraft with a distance less than the minimum safety separation.Conflict resolution aims to generate a conflict-free trajectory after the potential conflict is determined.Correspondingly,many deterministic methods have been studied to generate conflict resolution trajectory for interventions.The Dijkstra algorithm and the A*algorithm5need to build a model of environment before path searching,whereas methods such as the artificial field method6and the rapid random tree method7,8do not need a model of environment.Conflict resolution can also be solved as an optimal control problem or a convex optimization issue.9–11

With the increasing depth of the research,people are increasingly aware that uncertainties,such as wind gust,navigational error,and aircraft intent,are pervasive in current air traffic systems and have significant effects on the accuracy of TP.12A probabilistic method models uncertainties to describe potential variations by developing all possible future trajectories using a probability density function.13–19One approach is to predict the future position of an aircraft by using a stochastic model of the aircraft dynamics.Prandini et al.14used a stochastic kinematic model with uncertainties represented by a 2D Brownian motion.This approach does not require knowledge of the aircraft intent.However,the prediction error tends to increase quadratically with time.Moreover,this approach may be less accurate when a trajectory has maneuvers.Providing additional intent information may help reduce some of these uncertainties.An alternative approach is to add a position error to a nominal trajectory.20–23Based on the flight plan,aircraft dynamics,and wind data,some studies14,24,25computed a nominal aircraft trajectory by modeling aircraft dynamics using the stochastic linear hybrid system,in which the aircraft state vector is a continuous state and the aircraft flight model is a discrete state,and then a position uncertainty(or covariance)was added to the computed trajectory.This approach requires good knowledge of aircraft intents.

Correspondingly,trajectory planning has used many probabilistic methods,including probability map methods and intelligent methods,such as the genetic algorithm,particle swarm optimization,the neuralnetwork method,the simulated annealing method,antcolony optimization,the bee colony algorithm,and the memetic algorithm.26–32The aforementioned studies mostly treated an uncertainty as an open-loop problem in which an aircraft operates independently and controllers do not interfere with flight paths.

However,aircraft intent information could dynamically change over time in the context of 4DTBO,which allows an aircraft theflexibility of changing flight routes(or flight plans)in response to changing conditions,that is,theoretically,the aircraft can freely plan its trajectory while ensuring thatthe time constraintsofwaypointsare reached.33Although free does not refer to an absolute,no-constraint condition,the uncertainty of trajectory and the difficulty in TP are increased.Thus,the aircraft intent is difficult to describe with an accurate model,which presents a big challenge for CD&R.34

The new context of 4DTBO emphasizes the importance of time dimension,offering new perspectives in solving CD&R.Due to the difficulties in travel path prediction caused by the uncertainties of an individual purpose, Hagerstrand35originally transferred the study focus of individual travel path analysis from prediction of the individual purpose to analysis of the space–time range of individuals constrained by the environment,and proposed the concept of time geography.The time-geographical framework focuses on the behavioral possibilities of individuals.

Similarly,uncertainties caused by pilot intent increase dif ficulties in TP.Therefore,based on the theory of time geography,the study focus of aircraft conflict avoidance can be transferred from prediction of the flight trajectory of the aircraft to analysis of the influence of the 4D waypoint constraints on the space–time reachability of the aircraft activity.A novel pre-CD&R scheme based on the key elements of time geography,space–time path,and space–time prism is proposed.

In the proposed novel pre-CD&R scheme,the entire 4D trajectory of the aircraft is divided into a few route segments by a sequence of waypoints with CTAs.The CTAs must be satisfied during the entire travel lifecycle to ensure the safety of the overall air transport system.The process of an ordinary CD&R scheme TP–conflict detection–conflict resolution trajectory planning is transformed into potential path space calculation –space–time potential conflict space detection –conflict-free space–time trajectory planning in the novel pre-CD&R scheme.The flight support management system is designed to add a module that calculates the space–time reachability of each aircraft on each route segment between two waypoints in advance.The quantification of space–time reachability and Space-Time Potential Conflict Space(STPCS)offers an intuitive sight on the environment and surrounding aircraft states for the pilot and an optimal conflict-free trajectory as reference for pilots or air traffic controllers.The potential conflict probability is expected to decrease significantly.In addition,the application of the proposed pre-CD&R scheme is expected to help reduce the workloads of air traffic controllers because the responsibility of conflict resolution trajectory planning is delegated to an individual aircraft.

The rest of this paper is organized as follows.Section 2 presents the design architecture and process of the proposed pre-CD&R scheme,and elaborates the method for Space-Time Prism(STP)calculation and conflict detection by developing a case.Section 2.1 describes the developed case and assumptions.Section 2.2 demonstrates the application of space–time path in describing the flight plan.Section 2.3 shows how the airspace is discretized for further calculation.Section 2.4 describes the measurement theory for space–time reachability for aircraft and the calculation of space–time prism for aircraft.Section 2.5 introduces the method of conflict detection under the proposed pre-CD&R scheme.Section 3 elaborates the process of conflict-free Space-Time Trajectory(STT)planning using the Ant Colony Optimization(ACO)algorithm.Simulation is conducted and numerical results are analyzed in Section 4.Finally,Section 5 details conclusions,potential applications of the proposed pre-CD&R scheme,and directions for future research.

2.Trajectory prediction and conflict detection

In the context of 4DTBO,an aircraft will be allowed to perform air management operations,including conflict detection and resolution,self-separation,and flight plan changes.Therefore,an automation supporting system is needed to help the pilot and the air traffic controller in the decision-making process.28In this section,the design of a novel pre-CD&R scheme for this automation tool is considered.

2.1.Principle and architecture of the pre-CD&R scheme

The CD&R problem can be solved based on the perspective of time geography because an aircraft needs to pass a series of waypoints within CTAs according to the flight plan in the context of 4DTBO.The space–time path is one of the two key elements in the time geographical framework,and the other one is STP.In the proposed pre-CD&R scheme,the 4D trajectory of the aircraft can be described as the space–time path defined by a sequence of waypoints with CTAs.The necessary condition for conflict avoidance is that the space–time paths of multiple aircraft should have no intersection.TP takes pilot intent into account and can be transformed into aircraft reachability calculation.The reachability of the aircraft on each route segment can be measured by STP.The necessary condition for potential conflict avoidance is that the space–time path of one aircraft should not intersect with the STPs of other aircraft.The intersection of STPs is defined as STPCS,which reflects the space–time space with a conflict probability.The necessary condition for potential conflict avoidance of multiple aircraft is that the space–time path of each aircraft should not intersect with the STPCS.Conflict-free STT planning can be solved by finding an optimal space–time path outside the STPCS.

In the proposed pre-CD&R scheme,the uncertainty of pilot intent is accounted for via an STP for aircraft.Conflict detection is performed by verifying whether the STPs of aircraft intersect.The pre-CD&R scheme proposed based on time geography is expected to simplify the traditional decisionmaking process.As shown in Fig.1, firstly,aircraft send their flight plans,including a series of waypoints with CTAs,to the ATC center before departure.Then,the ATC center generates an STP for each aircraft according to the CTAs and velocity limits of aircraft,and calculates and shares the STPCSs in the ATC flight management supporting system by employing the proposed pre-CD&R scheme.The supporting system on each aircraft receives the relevant STPCS information within its lifecycle,and an optimized conflict-free STT is generated according to the pre-defined objective function,which is returned to the ATC center.The ATC center shares the STTs with the entire air transport system.Trajectory information shared between the aircraft,the airlines,and the ATC department facilitates collaborative decision-making and ensures the aircraft operation process to be visible,controllable,and achievable.

2.2.Case definitions and assumptions

A case of five aircraft situations was developed to illustrate in detail the proposed pre-CD&R scheme.According to the flight plan,Aircraft A is supposed to depart from Airport I at 9:00 and arrive at Airport II at 11:00 after 120 min of flying.During the flying process,the aircraft is required to pass through Waypoints 1,2,3,4,and 5 at 9:20,9:40,10:00,10:20,and 10:40,respectively.Table 1IThe developed flight plan is simplified for the convenience of analysis.In reality,the number of waypoints is normally more than that in this flight plan.shows the required passing waypoints and CTAs of the other four aircraft.Fig.2 shows the waypoints and airport positions.

Foranalyticalrequirements,wemadethefollowing assumptions:

(1)The initial flight plan is reasonable and feasible.

(2)Planning is based on a collaboration decision-making platform,that is,an aircraft share its real-time location,heading,velocity,destination,and otherrequired information.

(3)For simplification,we only concentrate on the cruising phase in the simulation study and assume that an aircraft does not alter its altitude because civil aircraft generally fly at a consistent altitude during the cruising phase.

(4)The CTA values are assumed to be fixed in this study to highlight the principle and calculation process of the proposed scheme.

2.3.Description of the flight plan by space-time path

Space-time path is the fundamental of time geography.The first step of the proposed pre-CD&R scheme is to describe the flight plan using the space–time path.In the flight plan,the continuous 4D trajectory of an aircraft is expediently described as several discrete waypoints with spatial–temporal information,including the position of the three spatial dimensions and the corresponding time.The 4D trajectory of an aircraft can be represented by a space–time path with time as thezcoordinate.For example,the space–time path of Aircraft APAcan be expressed as a set of a series of waypoints.Each waypoint is defined by its 3D coordinates,namely,longitude,latitude,and altitude,and a time-dimensional coordinate,which is the CTA of each waypoint.Fig.3 demonstrates how the flight plan information in Table 1 and Fig.2 can be described by space–time paths.

The set of five aircraft｛F｝ and the set of their space–time paths｛P｝are expressed as

Fig.1 Illustration of the pre-CD&R scheme.

Table 1 Flight plan for five aircraft.

Fig.2 Illustration of flight paths for five aircraft.

2.4.Airspace discretization

Airspace has to be discretized for further computation process.The grid method is used in this study to discretize the airspace,and the definition of neighbors is also introduced.The data structure of the algorithm is a third-order cube structure centered on the current stage,and the number of neighbors is 26,as shown in Fig.4.Taking the blue cube in the center as example,the red node represents the blue cube after discretization.The blue cube has 9 neighbors at the upperfloor,9 neighbors at the lowerfloor,and 8 neighbors at the samefloor.The size of the grid needs to be set according to the airspace scale.

2.5.Space-time reachability computation based on STP

Fig.3 Space-time paths for five aircraft.

Fig.4 Illustration of airspace discretization and adjacent nodes.

Space-time reachability describes the capability of an aircraft to reach waypoints in the airspace under the CTA constraint,which can be measured by the STP.The STP parameters for Aircraft A includeare the geographicallocationsofwaypointsrepresented bythe longitudeand latitude(and altitude,if needed)with constrained times of arrival,respectively.is the upper bound of the aircraft velocity.As shown in Fig.5,an aircraft must departure from waypointidenoted byat time,and arrive at waypointjdenoted byat timeThe aircraft can fly with a known andfinite maximum velocity.

Fig.5 STP of a single aircra ft.

The spatial extent that can be reached from a specific origin is limited by a circle with a radius of time limits multiplied by the maximum travelling velocity.The study uses a disc to represent all locations within the spatial extent.The left cone is the integral of the future disc on the time axis comprising all locations that can be reached from the origin waypoint during time-.The right cone is the integral of the past disc on the time axis comprising all locations that can be reached from the destination waypoint during time-.The intersection of the two cones is the STP of the aircraft,which describes the spatial extent of all possible locations between the origin and destination.

It is difficult to analytically describe the entire STP.However,it is easy to describe its spatial extent at a moment in time;this can serve as the basis for a wide range of prism analytics.An illustration of four different reachable extents is also demonstrated in Fig.5 by slicing the STP at different moments.The reachable extent at any timetis not a regular shape.At momentt,t∈）,the spatial extent of the STP for aircraft Ais the intersection of two convex spatial sets:(1)the future disc（t）comprising all locations that can be reached from waypointiby timet-,and(2)the past disc（t）encompassing all locations at timetthat can reach waypointjby time-t.

Fig.6 Comparison of STPs and PPAs of a single aircraft with different parameters.

Table 2 Different determinant values of STPs.

The Potential Path Space(PPS)in Fig.5 is the interior of the prism,which shows the spatial and temporal set of locations that can be reached by an aircraft from a specified location within a certain time interval.The PPS is a valuable measure of space–time reachability.The projection of an STP on thex–yplane is the Potential Path Area(PPA),which describes the physical reachable set of locations during timeand can be expressed as an ellipse,which is denoted by

Determinants responsible for the shape and size of the STP include the distance between the origin waypoint and the destination waypointDij,the time for the aircraft flying from the origin waypoint to the destination waypointtij,and the maximum velocity of the aircraftVmaxij.Fig.6 demonstrates the influences of different determinant values(Table 2)on the shape and size of the STP and PPA.

By analyzing the influences of the three determinants on the shape and size of the STP and PPA,it can be concluded that the size of the STP and PPA is positively related to the two determinants:the time limittijand the maximum velocityThe distanceDijdoes not influence the size of the STP and PPA.However,the distance has an effect on the shape of the STP and PPA.As indicates in Eq.(2),the distanceDijis negatively related to the b value of the PPA ellipse,so a larger distanceDijindicates a thinner STP and PPA.

A larger STP indicates a lower prediction accuracy of the potential path,which can increase safety but may reduce the airspace efficiency to a certain extent.Therefore,a reasonable velocity limit needs to be set to balance the efficiency of the proposed scheme and the airspace capacity.Boeing 737-600,one of the most commonly used aircraft,is taken as an example to conduct further analysis.According to the databaseofBoeing,themaximum cruisingvelocityof Boeing 737-600 is approximately 0.82 Mach(876 km/h),and itseconomicalcruising velocity isapproximately 0.785 Mach(838 km/h).36Noticing that a civil aircraft normally maintains a constant economical cruising velocity during cruise considering passengers’comfort,fuel assumption,and safety,a two-stage prism generation strategy that contains a preferred maximum velocity and an alternative is set up.On the first stage of prism generation,the economical cruising velocity is considered as a priority upper bound of the velocity during the cruise phase.If the preferred velocity fails to generate a prism within a given time limit,then the second stage will take the alternative(the maximum cruising velocity)as the upper bound.This two-stage prism generation strategy can not only improve the prediction accuracy for a potential path,but also ensure the feasibility of the following planned trajectory.

Fig.7 STPCS between two aircraft.

2.6.STPCS detection

In the proposed pre-CD&R scheme,the uncertainty of pilot intent is accounted for via space–time reachability computational,and conflict detection is performed by verifying whether the STPs of aircraft intersect.On the basis of STPs,the concepts of STPCS and Conflict-Free Potential Path Space(CFPPS)are introduced.The intersection of the STPs of aircraft is the STPCS,as shown in Fig.7.As an extension of the traditional definition of conflict detection,the STPCS demonstrates the geographical location of a potential conflict and the time of its occurrence.

After the STPCS is generated,the difference set between the STP and STPCS is defined as the CFPPS for further trajectory planning.Any aircraft thatflies along a space–time path within the CFPPS can avoid conflict.The CFPPS offers a reference for the pilot in trajectory selection according to the predefined economic objective,and also provides a feasible reference extent for conflict-free STT planning.

3.Conflict resolution

3.1.Problem description

Intheproposedpre-CD&Rschemeunderthetimegeographical framework,conflict resolution is performed by planning a conflict-free space–time trajectory avoiding an intersection.Conflict-free STT planning can be considered as a multiobjective path optimization problem within the contextual constraints of the CFPPS.Since the STPCS includes all the potential conflicts of the five aircraft,the planned conflict-free trajectory is expected to avoid the ‘domino effect’that happens frequently in multi-aircraft conflict resolution.

To generate an optimal conflict-free trajectory,the airspace has to be discretized first.The airspace is discretized into several grids in thex,y,andzdirections,respectively.A trajectory consists of a series of adjacent grid points.As demonstrated in Fig.4,the red point represents the current trajectory node of an aircraft.The next trajectory node must be generated among the expanded set of the 26 adjacent points.The ACO algorithm is used on the basis of airspace discretization tofind a series of discretized points that consists of an optimal trajectory.In addition,the size of the grid must be set according to the problem scale.A large grid leads to a low resolution and a low accuracy of the planned trajectory,and a small grid requires a large storage memory and calculation.Assuming that an airspace is restricted byxmin，xmax,ymin，ymax,andzmin，zmax,we set a grid size ofxgrid,ygrid,andzgridin thex,y,andzdirections,respectively.The number of total grids can be calculated as follows:

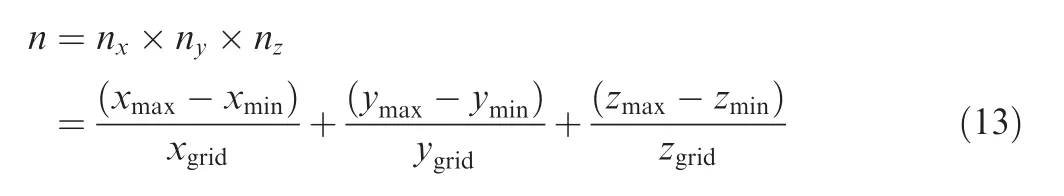
and the number of grid nodes coordinated by （ x，y，z）can be calculated as follows:

(1)Objective

During the conflict-free STT planning process,each aircraft can be regarded as an independent decision-making individual,and their selections of trajectory depend on their own objectives.The objective is an important part of trajectory planning,in which all factors that affect trajectory performance need to be considered.Generally,the trajectory planning objective needs to consider the following aspects.(A)Obstacles,restricted areas,danger areas,and potential conflicts that should be avoided.Therefore,the collision probability should be as low as possible.(B)The maneuverability of the aircraft,including turns and velocity changes,is also very important.(C)A shorter total length of planned trajectory indicates a more direct trajectory that needs less maneuver,less fuel assumption,and higher efficiency.The comprehensive performance of each trajectory should be measured to generate an optimal trajectory.The comprehensive index can be obtained by transforming the factors of all aspects into a dimensionless value that can be directly compared with one another.Consequently,the weight of each index should be determined.

(2)Constraints

Constrained by the physical limits and flying requirements of aircraft,the following constraints should be met when generating a trajectory.

(A)Maximum turning angle φ,which depends on the maneuverability of an aircraft. The horizontal projection of trajectory segmentiis represented as ai= ［xi-xi-1，yi-yi-1］T.The maximum turning angle constraints can be expressed as≥ cosφ ，i=1，2，...，n-1.

(B)Maximum economical cruising velocity.Normally,the

constraint of velocity depends on aircraft performance related to the dynamic system as well as the environment and position of the aircraft.The maximum performance velocity is not considered in our study because civil aircraft generally maintain an economical cruising velocity during thecruising phase.Instead,themaximum economical cruising velocity vmaxis crucial in this study.The velocity constraints can be expressed as≤v.max

(C)Time constraints.Three more constraints should be included because thez-axis represents the time in the space–time framework.In the geographical 3D condition,the expanded set of one node normally includes 26 adjacent nodes.However,in the space–time framework,as time cannot stop or retreat,theoretically the expanded set should exclude nodes of the following conditions:

a)Nodes withzcoordinate smaller than the current one denoted by （x，y，z-1）, （x+1，y，z-1）, （x-1，y，z-1）,（x，y+1，z-1）, （x+1，y+1，z-1）, （x-1，y+1，z-1）,（x，y-1，z-1）,（x+1，y-1，z-1）,（x-1，y-1，z-1）.

b)Nodes withzcoordinate equal to the current one denoted by （x+1，y，z）， （x-1，y，z）, （x，y+1，z）,（x+1，y+1，z）, （x-1，y+1，z）, （x，y-1，z）, （x+1，y-1，z）,（x-1，y-1，z）.

c)Nodes with the samexandycoordinates as the current ones simultaneously denoted by （x，y，z+1）.

Therefore,the expended set consists of 8 nodes denoted by（x+1，y，z+1）,（x-1，y，z+1）,（x，y+1，z+1）,（x+1，y+1，z+1）, （x-1，y+1，z+1）, （x，y-1，z+1）, （x+1，y-1，z+1）,（x-1，y-1，z+1）.

3.2.Conflict-free STT planning

The ACO algorithm was employed inthis study for conflict-free STT planning.ACO is a stochastic searching algorithm that simulates the real ant colony collaboration process based on the study of collective foraging behavior of real ant colony in nature.The solution path is optimized by leaving and exchanging pheromones on the solution path.ACO has excellent optimization searching performance because it combines the positive feedback mechanism,distributed computation,and greedy search function.37Positive feedback accelerates the search for a better solution.Distributed computation helps prevent premature convergence.Greedy searching reduces the searching time.The ACO algorithm has been widely used and achieved great performance in 2D and 3D path planning forrobots,underwatervehicles,and unmanned aerial vehicles.38–40In the proposed pre-CD&R scheme,some parameters of the algorithm need to be adjusted to meet the requirements of the space–time constraints under the time geographical framework.The ACO algorithm is set as follows.

(1)Cost function

According to the objective of civil trajectory planning,the cost function includes three parts,namely,total length of planned trajectoryPL,time of velocity changes ΔV,and distance to threatsDth,which is the sum of the distances between the discrete nodes of the trajectory and all the discrete points in the STPCS and threat area.These indicators need to be normalized by adding weight coefficientswl，wv，wd.The values of coefficients reflect the importance of each indicator during trajectory planning,and their sums are equal to 1,i.e.

To ensure the generated trajectory avoidance of potential conflicts to be the greatest possible,a penalty indicatorPis added to a trajectory that intersects with the STPCS,which means a trajectory that intersects with the STPCS will have a relatively large cost and is unlikely to be selected.This function can be easily modified to consider energy analysis and other operational costs according to the airline objective.

(2)Heuristic factor

The introduction of a heuristic factor is important to speed up the convergence rate of the algorithm.In our study,the heuristic factor is calculated using two conditions.For a node inside the STPCS,the heuristic value should be as small as possible to inspire the aircraft to avoid the STPCS.For a node outside the STPCS,the distance between the node and the STPCS and threat area can be used to design the heuristic function,which inspires the aircraft to select a node away from the STPCS and threat area.The heuristic factor for nodemcan be calculated as follows:

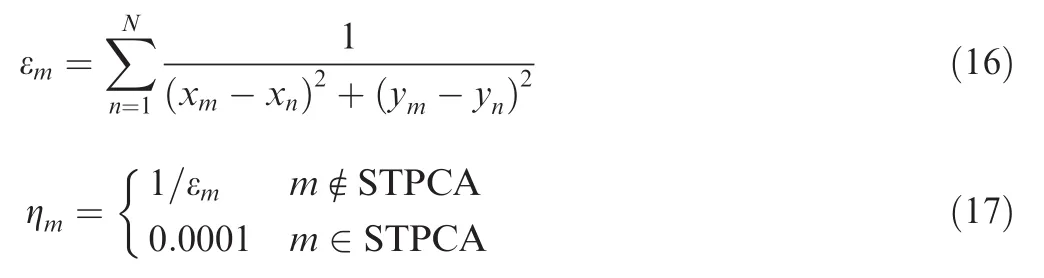
where （xn，yn）represents the nodes inside the STPCS;εmis the threat cost of nodem,which is the sum of inversed distances from nodemto all nodes inside the STPCS;ηmis the heuristic factor of nodem.The heuristic factor can accelerate the convergence of the algorithm.However,the weight of the heuristic factor should not be too large to prevent the pheromone from functioning because of its dominant role in ACO.

(3)Guidance factor

As ant colony optimization searches for an extension node accordingtothestatetransitionprobabilitybasedontheheuristicfactorsandpheromones,visibilityislimitedtothelocalscope because the heuristic values andpheromone values of neighbors have minimal differences,especially at the beginning of the iteration.Therefore,introducingaguidancefactortothestatetransition function is necessary,leading ants to move toward the target.The guidance factor for nodemcan be calculated as

where（xD，yD）is the position of the target node,λmis the guidance factor of nodem,anddmDis the distance between nodemand the target node.

(4)Pheromone matrix design and updating strategy

Annx×ny×nzsteps pheromone matrix τ is built according to the planning space and grid accuracy.ρ is the pheromone evaporation.The pheromone on all paths volatilized with each iteration can be expressed as （1- ρ）.The pheromone after each iteration can be expressed as

where Δτij（N）bestis the optimal path in theNth iteration,andQis the pheromone enhancement.is the cost of the optimal path in theNth iteration.Unlike the standard algorithm,our study only enhances the pheromone of the optimal path to improve the convergence rate of the algorithm.

(5)State transition strategy

Let τij（N）represent the pheromone from nodeito nodejin theNth iteration.At the beginning of the iteration,pheromones are the same on each path,that is, τij（0）=h(his a constant).Antk（k=1，2，3，...，M）determines the moving direction according to the probability determined on the pheromone,guidance factor,and heuristic factor.The probability of antkmoving from nodeito nodejin theNth iteration is expressed as follows:

where Allowedk=,in which Tabukis the Tabu list of antkin theNth iteration that consists of the nodes that are passed. α，β，γ are the weights of the pheromone,heuristic factor,and guidance factor,respectively.

The pseudo-code of the ACO algorithm for conflict-free STT planning under the time geography framework is demonstrated in Table 3.

4.Numerical results

To validate the proposed scheme of TP and CD&R under the time geography framework,several simulations were executed by developing a test set data.The simulations were executed on a Windows 7 Ultimate platform(64-bit)with a 2.6 GHz Dual Core processor and 4.0 GB RAM.The simulations were conducted in a 250 km×250 km airspace,and the time scale was 500 s.Through the analysis of the size and scale of the airspace and several attempts,the airspace was discretized into 12500 grids with a size of 5 km×5 km×10 s to balance the algorithm efficiency and optimization effect.

Table 3 Pseudo-code of the ACO algorithm for conflict-free STT planning.

Fig.8 Airspace and flying missions for five aircraft.

Table 4 Flight plans for five aircraft.

The air route structure of simulations was simplified according to a real airspace captured in the Northern China,because the image of the real airspace cannot be exposed for secrecy consideration.In addition,the origin and destination waypoints of thefight plans of five aircraft were extracted from FlightAware,a website that tracks commercial flights all over the world in real time.Fig.8 shows that the five aircraft are flying their own missions through predetermined waypoints within certain time constraints.OA,OB,OC,OD,OEandDA,DB,DC,DD,DErepresents the origin and destination waypoint of Aircraft A,B,C,D,E,respectively.Aircraft A was assumed to fly from its origin waypointOA,denoted by(120,90),at time 20 s to the destination waypointDA,denoted by(120,130),at time 300 s.Similarly,the flight plans including the coordinates of waypoints and CTAs for the other aircraft are listed in Table 4.Some of them may encounter conflicts.Theaircraftparametersandaerodynamicdatacanbe extracted from EUROCONTROL Base of Aircraft Data.36A typical loaded Boeing 737-600 aircraft with a maximum cruising velocity of 0.82 Mach(876 km/h)and an economical cruising velocity of 0.785 Mach(838 km/h)was assumed to fly the missions.IIIWe assumed that the five aircraft are the same type with similar economical cruising velocities in this case,but it is available for any type of aircraft with different parameters.

4.1.STP computation and STPCS detection

To calculate the space–time reachability of the five aircraft and provide a reference for further conflict-free STT planning,the PPAs and STPs of the five aircraft,as well as the STPCSs between them,were calculated by using the proposed scheme,which are demonstrated in Figs.9 and 10.

Table 5 presents the scales of the STPs of the five aircraft.Table 6 lists the scales of the STPCSs among the five aircraft.

Table 5 shows that the STP of Aircraft C is the largest because its mission is characterized by a shorter distance(36.1 km between the origin and destination waypoints)with a relatively longer time interval(330 s).This type of flight plan allows aircraft detours far away from the origin waypoint while ensuring an arrival at the destination waypoint in time.On the contrary,the STP of Aircraft D is the smallest because its mission is characterized by a longer distance(72.1 km between the origin and destination waypoints)with a relatively shorter time interval(380 s).This type of flight plan requires aircraft to fly along a shorter path with a higher velocity from the origin waypoint to meet the CTA of the destination waypoint.

Table 6 shows that the possibility of a potential conflict between Aircraft B and C(B-C)is greatest,since the geographical locations and CTAs of the departure and destination waypoints of missions B and C are relatively close to each other.IIWe assumed that the five aircraft are the same type with similar economical cruising velocities in this case,but it is available for any type of aircraft with different parameters.t is noteworthy that although missions C and D also have close geographical locations and CTAs of the departure and destination waypoints,the STPCS between Aircraft C and D(C-D)is small because of the small STP of Aircraft D.

4.2.Conflict-free STT planning

The conflict-free STT can be generated using the ACO algorithm based on the results of the STPs and STPCSs for the five aircraft.Table 7 shows the parameters of the ACO algorithm for conflict-free STT planning under the proposed scheme.

The algorithm was performed for 2-to 6-aircraft scenarios,respectively,and all of them achieved ideal conflict free trajectory.However,only the five-aircraft scenario was elaborated below considering the length of the article.Tables 8 and 9 provide the execution time,actual planned trajectory length,and cost,including penalty for the planned trajectory for twoand five-aircraft scenarios,respectively.The actual trajectory length is the sum of the squares ofxandybetween two nodes instead ofx,y,andz.

To analyze how the algorithm scales with the scenario size and spatial discretization,the algorithm was performed in twoto six-aircraft situations.In addition,the airspace was discretized into the following five degrees:15625 grids with a size of 10km×10km×20s,31250 grids with a size of 10km×10km×10s,62500 girds with a size of 10km×10km×5s,125000 grids with a size of 5km×5km×10s,and 250000 grids with a size of 5km×5km×5s.Each situation was performed three times to achieve an average execution time.As illustrated in Fig.11,the algorithm execution time increases linearly with the scenario size.In addition,Fig.12 indicates that the algorithm efficiency is exponentially related to the degree of spatial discretization.Therefore,it is necessary to set the degree of discretization according to the problem scale.

Fig.9 PPAs of five aircraft.

Fig.10 STPs and STPCSs of five aircraft.

Table 5 Scales of STPs of five aircraft.

Figs.13 and 14 show that the lengths and costs of the actual planned trajectories for Aircraft A,B,C,and D gradually converge with iterations.All values approximately converge to the global minimum after 20 iterations,indicating that the algorithm is effective and feasible.The values of the length and cost of the actual planned trajectories of aircraft E show no variation with iterations because the STP of aircraft E does not intersect with that of any other aircraft.

Figs.15 and 16 present the simulation results of STPs and the actual planned trajectories for the five aircraft using the ACO algorithm with 40 ants and 100 iterations when the algorithm has converged and achieved the global optimum.None of the planned space–time trajectories intersected with one another.

The proposed pre-CD&R scheme is verified to be effective in generating optimal conflict-free STT.It has the following advantagescompared with otherprobabilisticmethods including probability map and intelligent methods.Firstly,most of the existing studies can achieve a relatively ideal solution for two-aircraft conflict resolution.However,for multi-aircraft situations,the algorithm tends to be complexand time-consuming.The proposed pre-CD&R scheme has no advantage in the execution time compared with some optimal methods when solving two-aircraft conflicts,but it is expected to save a large amount of time in considering multi-aircraft conflicts because it can solve conflicts of multiple aircraft simultaneously.Secondly,the proposed pre-CD&R scheme is expected to improve the robustness of a solution that considers multi-aircraft conflicts,because the generation of conflict-free STT is designed to avoid all potential conflicts.Moreover,it could avoid a potential ‘domino effect’of the conventional method.The pre-CD&R scheme is able to offer a guidance reference for pilots,which can not only keep a safe distance between aircraft,but also consider the preference of airlines during a trajectory planning process.

Table 8 Results of two-aircraft scenario.

Table 6 Scales of STPCSs among five aircraft.

Table 9 Results of multi-aircraft( five)scenario.

Fig.11 Relation between execution time and the scenario size.

5.Conclusions and future work

Fig.12 Relation between execution timeand degreeof discretization.

Fig.13 Convergence curves of actual trajectory lengths for five aircraft.

The context of 4DTBO brings the uncertainty of pilot intent into our sight,which reduces the TP accuracy and increases the difficulty of CD&R.The conceptual design of a novel pre-CD&R scheme that considers the uncertainty of pilot intent was presented,providing CFPPS and optimal conflictfree STT for pilots and air traffic controllers to support future 4DTBO.A functional architecture of the pre-CD&R scheme was described.Principles and methods were elaborated to calculate the STP,STPCS,and CFPPS.The ACO algorithm was adopted to generate a conflict-free STT.Simulation case studies were performed for 2-to 6-aircraft scenarios based on a real airspace scenario and real-time flying data.Results demonstrated the functional capability of the pre-CD&R scheme in generating conflict-free space–time trajectory satisfying the contextual constraints and airlines’cost-effective objectives.

The main contributions of the proposed pre-CD&R scheme can be summarized as follows:

(1)The proposed scheme offers a potential novel approach in solving the conflicts of multiple aircraft simultaneously and avoiding the follow-up influence(domino confl ict)in multi-aircraft conflict resolution.

(2)The proposed scheme is able to ensure the CTAs of waypoints with considerations of pilot intent and airlines’benefit.It is also expected to reduce the workloads of air traffic controllers by delegating the responsibility of conflict resolution trajectory planning from air traffic controllers to individual aircraft.

(3)The proposed scheme originally introduces the concept of time geography into air traffic management and presents the measurement of STP for aircraft in a specific air transport environment.

Fig.14 Convergence curves of costs for five aircraft.

Fig.15 Actual planned space–time trajectories for five aircraft.

To clearly demonstrate the essence of the proposed scheme,this study only demonstrates the application of the proposed scheme in a 3D situation without altitude altering.However,the proposed scheme can be easily applied to a 4D situation with altering altitude and dynamic restriction area.Further study intentions include the descriptions of the STP,STPCS,and other related elements in 4D as well as a deeper analysis of the constraints in vertical and horizontal directions.

In addition,the CTA value is assumed to be fixed in this study to highlight the principle and calculation process of the proposed scheme.However,a CTA with a time window should be more suitable for a real-world situation.Further study will replace the CTA with a time window and enhance the applicability of the proposed scheme.

Fig.16 Actual planned trajectories for five aircraft.

Acknowledgements

The authors acknowledge the anonymous reviewers for their valuable comments and suggestions.The authors would also like to acknowledge thefinancial support from the Civil Aviation Joint Funds of the National Natural Science Foundation of China(No’s.U1533203,61179069).