A new hybrid aerodynamic optimization framework based on differential evolution and invasive weed optimization
2018-07-24ZijingLIUXuejunLIUXinyeCAI
Zijing LIU,Xuejun LIU,Xinye CAI
College of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China
KEYWORDS Airfoil design;Differential evolution;Genetic algorithms;Invasive weed optimization;Optimization
Abstract Since many aerodynamic optimization problems in the area of aeronautics contain highly nonlinear objectives and multiple local optima,it is still a challenge for most of the traditional optimization methods tofind the global optima.In this paper,a new hybrid optimization framework based on Differential Evolution and Invasive Weed Optimization(IWO_DE/Ring)is developed,which combines global and local search to improve the performance,where a Multiple-Output Gaussian Process(MOGP)is used as the surrogate model.We first use several test functions to verify the performance of the IWO_DE/Ring method,and then apply the optimization framework to a supercritical airfoil design problem.The convergence and the robustness of the proposed framework are compared against some other optimization methods.The IWO_DE/Ringbased approach provides much quicker and steadier convergence than the traditional methods.The results show that the stability of the dynamic optimization process is an important indication of the confidence in the obtained optimum,and the proposed optimization framework based on IWO_DE/Ring is a reliable and promising alternative for complex aeronautical optimization problems.
1.Introduction
Many aerodynamic optimization problems are characterized by highly nonlinear objective functions with various constraints,wide design space and multiple local optima.It is thus challenging tofind the global optima for these problems.Airfoil design optimization approaches have attracted a great amount of attention over decades,which use different shape representation methods and surrogate models to approximate the nonlinear relationship between airfoil geometry and aerodynamic performance,coupled with different optimization methods tofind the global optimum.1In addition to the prediction accuracy of surrogate models,the optimization methods are also playing an important role in the entire airfoil optimization process.An optimization algorithm suitable for all of the characteristics of airfoil optimization problems and capable of always finding the most likely optimal solution can improve the aerodynamic performance and shorten the design cycle.
In general,the optimization algorithms are divided into two categories,deterministic algorithms and probabilistic algorithms.Deterministic algorithms are those who always yield the same outputs for the same inputs.2Gradient-based Methods(GMs)3are a category of deterministic algorithms widely applied for airfoil design4–7,which have the advantage of fast convergence.However,GMs are very sensitive to initialization,resulting in high possibility of plunging in local optima in multiple-local-minimaoptimization problems.And it requires the design space to have continuous first derivatives for gradient calculation,which limits the efficient use of gradient-based methods in engineering.8,9Probabilistic algorithms,including Simulated Annealing(SA)10,Genetic Algorithms (GA)11,Particle Swarm Optimization (PSO)12,Differential Evolution(DE)13and so on,have drawn more attention to tackling optimization problems in aerospace field.For example,SA has been applied in aerodynamic optimization of an axisymmetric forebody,where SA shows great advantage of overcoming the limitations of GMs.14,15But the search in SA is performed by a hill climbing method,and easily gets trapped in local optima as GMs do.9DE coupled with polynomial chaos methods is selected in the computational aerodynamic design process as the basis for both the single-and multi-objective algorithms because of its easy implementation and high efficiency.16To overcome the drawbacks of GMs,PSO is also used to optimize the flow control applied to the transonic flow past an airfoil,showing efficiency of providing a more global solution.17Among these probabilisticalgorithms,GAsareprobablythemostwidely used.18–25Their robustness and easy implementation have made them good tools to tackle such complex problems in airfoil design,regardless of such difficulties as the mixing of discrete and continuous variables and the presence of multiple local optima.26But GAs usually require large population size and amount of generations for evolution27,resulting in high computational costs to search the optimal solution in a very large airfoil design space,which leads to several variants coupled with neural network28,29or GMs.27,30,31
Invasive Weed Optimization(IWO)32algorithm is an intelligent optimization algorithm inspired by natural weed evolution.The algorithm is an adaptive local search that can avoid the waste of computational resources in searching the undesirable infeasible region and thus leads to a good evolutionary direction under the guidance of high- fitness individuals.To complement with IWO as the local search,DE algorithm was used as the global search component.33Based on the previous work,an improved weed algorithm(IWO_DE/Ring)34was proposed,where a ring neighborhood topology is used to enhance local search ability.This new method provides a good balance between effective exploration and efficient exploitation.However,the performance of the algorithm has not been verified in the field of aeronautics such as airfoil design problems.
In the airfoil design involving surrogate models,optimization solutions also depend on the model accuracy.In order to improve the accuracy of the surrogate models,the optimization frameworksusually contain many iterations.The obtained optimal profiles at previous iterations are included in the training data from which new surrogate models are built for further iterations.With an accurate initial surrogate model and a reliable optimization algorithm,the optimum for each iteration should ideally converge steadily to the global optimum as the optimization process proceeds.In static optimization problems,the statistical dispersion of the results obtained in multiple runs is an important characteristic to be considered.27Analogously,in this dynamic airfoil design the variation of the optimum found in each iteration should be monitored in order to acquire a level of confidence in the obtained optimum.
In this study,we propose a new optimization framework which utilizes IWO_DE/Ring optimization method and a Multiple-Output-Gaussian-Process (MOGP) surrogate model.35This surrogate model is able to capture the correlations between the outputs and has been proved to increase the prediction accuracy in airfoil optimization problems where significant correlations among lift,drag and moment coef ficients have been observed.35We first use several test functions to test the performance of the IWO_DE/Ring method,and then apply the optimization framework to a supercritical airfoil design problem.For both cases,the convergence performance is compared against those of other different methods.The purpose of this study is to show that the stability in the optimization process is an important indication of the con fidence in the obtained optimum,and the proposed optimization framework is a reliable alternative in optimal airfoil design.
The rest of this paper is organized as follows.Section 2 introduces the methodology of IWO and IWO_DE/Ring,and a demonstration to testify the robustness of IWO_DE/Ring compared with GA and IWO on several test functions.Section 3 proposes a hybrid optimization framework and describes its application in airfoil design.Several experiments are presented to compare the optimization process of the proposed framework with other alternatives in Section 4,which is followed by the conclusions and discussion in Section 5.
2.Methods
2.1.Invasive weed optimization
Before introducing the improved version of IWO,we give a brief review of the original IWO.Generally,an IWO algorithm contains the following four steps:
(1)Population initialization
A certain amount of weeds are scattered uniformly and randomly in the givenndimensional search space.
(2)Reproduction
Each individual of the population reproduces different numbers of seeds,Si,depending on its normalized fitnessfiand the permissible maximum and minimum numbers of seedsSmaxandSmin.Siis formulated as
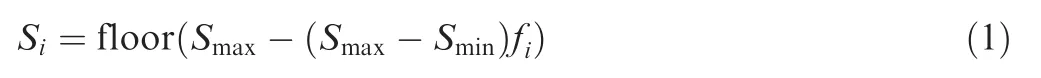
where the normalized fitnessfiis defined by its own fitness,the highest fitness and the lowest fitness of the population as

(3)Spatial dispersal
The seeds are dispersed randomly around their parents in normal distributions with zero mean and decreasing standard deviation sd from a predefined initial value sdmaxto a predefi ned final value sdminas the iteration proceeds.The value of sd for a given generation is calculated by

where iter is the current number of generations,itermaxis the maximum one,andmis the nonlinear modulation index.
(4)Competitive selection
The number of individuals will finally reach the maximum for generations of breeding.Therefore,a selection mechanism is adopted by choosing weeds with high fitness to be preserved into the next generation.Then the steps(1)–(4)are repeated until a satisfactory state is reached.
2.2.Hybridization of DE and IWO
In IWO,only individuals with high fitness values are permitted to reproduce offsprings,and the number of offsprings is determined by the normalized fitness value.Therefore,IWO is able to avoid wasting time on searching the less feasible region in a constrained optimization problem.33However,as a local search algorithm,IWO is sensitive to the initial values of the parameters and easily gets trapped into local optima.
A modified version of DE is combined with a novel IWO variant for the aim of acquiring the balance between effective exploration and efficient exploitation in Ref.34,utilizing a ring neighborhood topology.36–38A multi-objective optimization technique based on Pareto optimality39is employed to solve single-objective optimization problems with constraints,where the constraint satisfaction is transformed to another objective coupled with the original objective to be optimized to balance between the feasibility and objective function.33,34The details ofthe improved invasive weed optimization method,IWO_DE/Ring,are described as follows.
2.2.1.Invasive weed optimization variant for local exploitation
The original IWO leads to a coarse-grained local search because the offsprings have the same dispersal degree in all dimensions at a certain iteration.Therefore,the dispersal degree of offsprings in IWO variant is determined by the estimation of the neighborhood information around their parent based on the ring neighborhood topology,which is more powerful in local search compared with the original IWO.The formula of the dispersal operator is given as

where abs(·)is an operation of computing absolute value,xiis theith weed,and xjis thejth neighborhood of xi.Besides,niis the number of neighborhoods xihas andfjis the fitness of xjcomputed by Eq.(2).
After reproduction,a diversity mutation proposed in Ref.40is employed for a high diversity of the population:
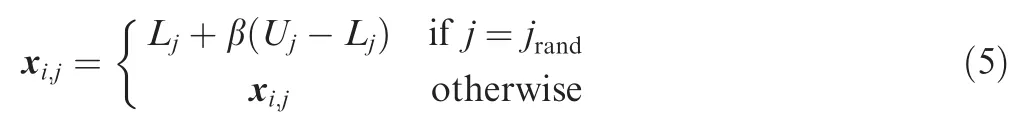
wherei=1,2,...,Nandj=1,2,...,n,denoting theith individual of the population and thejth characteristic of the individual respectively;LjandUjare the lower and upper bounds of thejth characteristic respectively;β is generated within[0,1]randomly and uniformly;jrandis an integer selected randomly within[1,n].
As generations continue,the population size will reach the maximum.A non-dominated sorting method41is employed to eliminate the individuals undesired,in which individuals in lower non-dominated front and with smaller constraint violation value are preserved to the next generation.
2.2.2.Differential Evolution variant for global exploration
DE13is a simple and powerful global optimization algorithm for its excellent and efficient performance.Generally,DE is executed in the process of evolution including initialization,mutation,crossover and selection.The following are some details of a variant of the original DE.34
Mutant strategies are various42,while the form of the mutant vector viselected in IWO_DE/Ring is

wherer1andr2are selected uniformly and randomly within[1,N],xibestis the best individual among the neighborhood organized by the ring neighborhood topology,andFis a scaling factor that measures the scale of the difference between vectors.
In crossover operation,a trial vector uiis generated by inheriting the characteristics of viand xiand it is given as

where randjis a random number,andCris the crossover probability parameter.The values of randjandCrare both within[0,1].
Different from the original DE,the selection operation of DE variant is based on the concept of Pareto dominance.The infeasible solution with the maximum amount of constraint violation or the feasible solution with the maximum objective function value is selected to be replaced.For detailed information about the DE variant,readers can refer to Ref.34.
2.2.3.Algorithm description of IWO_DE/Ring
The entire process of IWO_DE/Ring hybridizing IWO variant and DE variant to exert the efficient exploitation and effective exploration is presented in Table 1.
2.3.Demonstration of robustness of IWO_DE/Ring
We use several test functions(Egg holder function43,44,Rastrigin function45,Griewank function43,45,and Mishra’s bird function with a nonlinear constraint44)to evaluate the performance of GA,IWO and IWO_DE/Ring,for their characteristics of complex relationships between variables and function values.The details of these functions are given in Table 2.It is obvious that there are regular or irregular fluctuations with many troughs in all cases.

Table 1 Procedures of IWO_DE/Ring.
Given the identical maximum number of Function Evaluations(FEs)as 60000,we compare the convergence trends and resultsofGA,IWOandIWO_DE/Ringforthefour test-function-optimization problems.The detailed parameter settings for the three methods are presented in Tables 3–5,respectively.Each optimization method performs 20 independent runs with different initializations to obtain statistical evaluation of its performance for each problem.Fig.1 displays the box plots of the function values and the corresponding variables optimized by each algorithm.The upper and lower limits,the median,and the 25th and 75th percentiles of the optima are shown in the plots.One can observe that optima obtained by GA are easily scatteredly distributed over the variable spaces for all test functions,occasionally converging to the known global optima.IWO has the largest variance of optima for Egg holder function but almost converges to the global optima for both Rastrigin and Mishra’s bird functions in each run,which indicates that the performance of IWO is also influenced by the fluctuation characteristics of the functions to a certain degree.However,the optima of IWO_DE/Ring are distributed over the specific regions closely around the global optima for all of these functions.Here,Egg holder function is taken as an example,and Fig.2 shows the independent optimization progresses of the three methods.It indicates that all the methods can get into some local optima in early generations.Almost all the independent runs for IWO_DE/Ring are able to escape them and converge to the global optimum later,while those for GA and IWO fail to.It is remarkable that IWO_DE/Ring shows outstanding stability in converging to global optima for its hybridization of a globalsearch algorithm DE and a local-search algorithm IWO.It is thus always able to explore the vicinity of the global optima,and exploit the ideal optimal solutions.
These examples show the superior robustness of IWO_DE/Ring in dealing with highly nonlinear optimization problems with multiple local minima.For complex airfoil design problems with wide design space as well as highly nonlinear objective functions and constraints,IWO_DE/Ring is likely to have better performance on the search of global optima.

Table 2 Test functions.

Table 3 Parameter setting of GA.

Table 4 Parameter setting of IWO.
3.Airfoil design based on hybrid optimization framework using IWO_DE/Ring
3.1.Hybrid optimization framework
Considering the robustness of IWO_DE/Ring,and the accuracy of MOGP which we have verified in our previous work35,we propose a new optimization framework utilizing these two approaches to achieve optimal results.The optimization framework is presented in Fig.3,which contains 6 steps:
(1)Use Class/Shape-function-Transformation (CST)parameterization46to describe the shape of an airfoil,and assign upper and lower bounds of the design variables.
(2)Sample design points using Latin Hypercube Sampling(LHS)47in design space based on the design variables.
(3)Compute the aerodynamic parameters of these design points utilizing Computational Fluid Dynamics(CFD)method.
(4)Construct a MOGP surrogate model to approximate the nonlinear relationship between design variables and aerodynamic responses.
(5)Apply the IWO_DE/Ring algorithm on the surrogate model tofind the global optimum and the corresponding design variables.
(6)Verify the solution by comparing with CFD results,and add the verified airfoil profile into the samples to construct a new model.
The whole process is iterated until the solution is converged or the process reaches the maximum number of iterations.Thefinal optimal airfoil can be found in the external archive after convergence.
The optimization framework is verified using an optimization example of the RAE2822 supercritical airfoil.The constrained nonlinear optimization problem can be expressed as follows:

whereRDis the design space.CL,CDandAare the lift coefficient,drag coefficient and cross-sectional area of the airfoil,respectively.The variables with subscript 0 are those corresponding to the original airfoil RAE2822.LandUare the lower and upper bounds of the airfoil representation parameters,respectively.
3.2.Experimental setup
It has been proved that 4th–6th order Bernstein polynomials are suitable for describing airfoils.48So we use 5th-order Bernstein polynomials for both the upper and lower surfaces to balance the accuracy of parameterization and the complexity of design space,for which there are thus 12 CST parameters for each airfoil.
We aim to improve the lift-to-drag ratio of the RAE2822 airfoil without significant changes of the lift coefficient and the cross-sectional area,for which the Reynolds number isRe=6.5×106,the Mach number isMa=0.73 and the angle of attack is α =2.79°,a modified condition of Case 9 for RAE2822 in Ref.49.We generate a series of meshes with different numbers of elements to be chosen for the later experiments.The global and local views of these meshes are shown in Fig.4,and the drag coefficients computed utilizing corresponding meshes are given in Table 6.The meshes with coarse distributions at the leading edge of the airfoil,such as those with 14522 and 29316 elements,lead to very bad resolution of drag coefficients,while the meshes with more points at the leading edge,like those with 53756 and 75342 elements,involve substantially uniform drag coefficients with high accuracy,compared to the computation results in Ref.50for the same Case 9.Therefore,we choose the mesh with 53756 elements in the entire domain for optimization.

Fig.1 Convergence results of GA,IWO and IWO_DE/Ring for test functions.

Fig.2 Optimization progress of GA,IWO and IWO_DE/Ring for Egg holder function.

Fig.3 Optimization framework.
The lift and drag coefficients of the airfoils are calculated by solving the Navier-Stokes equations based on density,utilizing thefinite volume method,for which the Spalart-Allmaras turbulence model is employed.The discretization scheme is selected as first-order upwind.
The MOGP surrogate model takes a number of airfoil profi les,each of which is represented by 12 CST parameters as inputs and by corresponding lift coefficients and drag coef ficients as outputs,and approximates the nonlinear relationship between design variables and aerodynamic responses.In order to guarantee the accuracy of the surrogate model,we sample 500 initial design points randomly and uniformly from the design space and construct a model with an accuracy of 93.84%in drag coefficient and 98.39%in lift coefficient.The original RAE2822 airfoil and the 500 samples are presented in Fig.5.
In order to testify the performance of the proposed optimization framework,we compare it with other optimization approaches which replace the optimizer in our framework with IWO and the widely-used GA,respectively.For GAs,obtained optima heavily depend on parameter setting.Considering highly nonlinear objectives and constraints with possible multiple local optima involved in airfoil design problem,the maximum number of iterations(Generations)and the individual number in each generation(PopulationSize)are adjusted to 1400 and 200,respectively.The parameter settings in IWO and IWO_DE/Ring are the same as shown in Tables 4 and 5.
4.Results and discussion
4.1.Performance verification of static optimization iteration
A robust optimization algorithm is supposed to converge to the same optimum even with different initializations for multiple runs and is thus able to gain a high level of confidence in the obtained optimum.The robustness of the optimization algorithm is thus vital to guarantee the convergence of the optimization framework for airfoil design problem associated with complex design space and possible multiple local optima.Before evaluating the performance of the proposed airfoil design framework,we test the stability of single iteration within the framework using a statistic optimization example.We conduct 20 independent runs with different initializations for GA,IWO and IWO_DE/Ring,respectively,based on the same static surrogate model and do statistical analysis of the obtained optima for each method.
The box plots of the obtained optimal lift-to-drag ratio for the single iteration in the framework using GA,IWO and IWO_DE/Ring are presented in Fig.6.GA converges to the most widely distributed optima among the three methods,varying between 45 and 72 in independent runs.IWO obtains smaller distribution range of optima than GA and all obtained optima are greater than 70.All runs of IWO_DE/Ring converge to the same optimum ofCL/CD=74 except an outlier of 73.Fig.7 shows the box plots of the 12 CST variables obtained by the 20 runs of the three optimization methods,where all optimal variables obtained using GA and IWO are distributed wider than those obtained using IWO_DE/Ring.
From this example,it can be observed that both GA and IWO methods are impressionable to initial populations and easily get trapped into local optima.On the contrary,IWO_DE/Ring combines the global search method DE with the local search method IWO,and this example shows clearly its advantage of both effective exploration and efficient exploitation.From this point of view,the robust iterations in our optimization framework are likely to lead to an overall steady convergence in the dynamic airfoil design,which is shown in the next section.

Fig.4 Example meshes with different numbers of elements for RAE2822.

Table 6 Drag coefficient comparison of RAE2822 with different meshes.

Fig.5 Sampling space and the original RAE2822 airfoil.
4.2.Performance comparison of optimization algorithms in dynamic airfoil design
Ideally,a stable and outstanding optimization algorithm is easily able to converge to the vicinity of the true global optimum under the premise of a high-accuracy model at each iteration.By adding the optima obtained at previous iterations into the training data from which new models are built for further iterations,the prediction accuracy of the model near the global optimum will be improved to guarantee the convergence of the whole optimization framework.We compare the performance of our optimization framework with the one adopting GA and monitor the variation of the obtained optima as the optimization framework progresses.

Fig.6 Box plots of CL/CDoptimized by GA,IWO and IWO_DE/Ring.
Fig.8 shows the converged optimum and the corresponding true target value obtained from CFD computation at each iteration.The green and the red dot-dash lines represent the optimization processes of IWO_DE/Ring and GA respectively.The solid lines represent the variation of the related CFD computations for optima.Given the same initial surrogate model at the first iteration,both optimization methodsfind the relatively high optima.The disagreement between the optimum and the true target value is high for both methods due to the low accuracy of the initial surrogate model around the global optimum.Since the surrogate model at the following iterations is updated using the obtained true profile and the accuracy of the surrogate model around the global optimum increases,the discrepancy between the converged optima and the true target values should decrease iteration by iteration till convergence.It can be seen in Fig.8 that the subsequent optima obtained from IWO_DE/Ring keep decreasing,while the corresponding true target values tend to ascend accordingly.From the 11th iteration on,the optimum and the corresponding true target reach a general agreement,except for an outlier in the 18th iteration caused by the low accuracy of the model at the latest converged optimum.This indicates that the global solution is reached and a high level of confidence associated with the obtained global optimum is also obtained.However,for the reason that GA converges to different local optima in each iteration,it is not a surprise to observe that there is high randomness in both optima and true target values within the 25 iterations.Even the algorithm occasionally converges to the global optimum,the surrogate model cannot be polished continually in the subsequent iterations and one cannot observe a significant convergence.Also,no confidence can be obtained and associated with any obtained optimum for GA approach.

Fig.7 Box plots of variable values optimized by GA,IWO and IWO_DE/Ring.

Fig.8 Variation of optima and true target values at iterations.
From this example,wefind that our optimization framework obtains a quick convergence and a confident solution for the airfoil design problem.
4.3.Obtained airfoil
After the surrogate model is converged,the optimal airfoil of the highest lift-to-drag ratio for our framework can be found in the 16th iteration(see Fig.8).Table 7 shows the improvement in the aerodynamic performance of the optimal airfoil compared with the original RAE2822,and the corresponding design variables with the upper and lower bounds are presented in Table 8.It can be observed that the drag coefficient is greatly reduced while respectively maintaining the lift coef ficient and the cross-sectional area at a certain level,resulting in a significant increase in lift-to-drag ratio by 29.34%from 45.5460 to 58.9091.The geometry comparison between the original RAE2822 and the optimal airfoil is presented in Fig.9,while their corresponding pressure coefficientCpdistributions are presented in Fig.10.From Figs.9 and 10,we can observe a reasonably close match between the shapes and theirCpdistributions.Compared with the original RAE2822,the radius at the leading edge decreases,and the shock is signi ficantly weakened as expected.This shows that the proposed optimization framework is feasible and effective for airfoil design.However,the optimal airfoil depends on various factors including the number of initial samples,the design space defined by the boundaries of the representation parameters,the accuracy of the surrogate model,the form of the objective functions and constraints,and so on.Any of them can affect the final result.For all these possible reasons,the optimal result still has a very weak shock wave due to the limited number of initial samples and the fixed design space in this paper.However,the aerodynamic performance of the optimal airfoil is not the main concern in this work but an auxiliarydemonstration of the feasibility and robustness of the proposed framework to solve complex nonlinear problems.

Table 8 Design space and variable values of RAE2822 and optimal airfoil.

Fig.9 Shape comparison between RAE2822 and optimal airfoils.

Fig.10 Cpdistribution comparison between RAE2822 and optimal airfoils.

Table 7 Aerodynamic performance comparison between RAE2822 and optimal airfoil.
5.Conclusions
In this contribution,we develop a new optimization framework by coupling IWO_DE/Ring and a multiple-output-Gaussianprocess surrogate model,and test its performance using a computer simulation example of supercritical airfoil optimization through an engineering problem.The adopted IWO_DE/Ring optimization method in our framework combines a globalsearch DE algorithm and a local-search IWO algorithm to achieve a good balance between the effective exploration and the efficient exploitation.We first compare the distribution ranges of the optima obtained from multiple independent runs of a single iteration within various optimization frameworks using GA,IWO and IWO_DE/Ring,respectively,based on the same static surrogate model.The iterations in our framework almost converge to the same optimum with ideal lift-todrag ratio value starting from different initial populations,showing the stability of the method when applied to the airfoil design problems.We next compare the performance of the optimizationframeworksadoptingGAandIWO_DE/Ring,respectively,and monitor the variation of the optima as the optimization frameworks progress for a supercritical airfoil design starting from RAE2822.From the monitored optimization progresses,we cannot observe a clear convergence of GA-based method as there is high randomness existing in the optimum for each iteration.However,our method converges quickly and obtains a high level of confidence associated with the converged global optimum.Finally,we compare the obtained optimal airfoil with the original RAE2822.There is an increase in lift-to-drag ratio by 29.34%from 45.5460 to 58.9091,which provesthe feasibility ofthe proposed optimization framework.
One of the difficulties associated with airfoil optimization is the possibility of multimodality in the design space.Chernukhin and Zingg51conducted an airfoil optimization example without the aid of surrogate model.They reported that the design space is unimodal,for the reason that three out of four optimization algorithms fail in finding additional local optima,and the result is immune to the number of design variables,Mach number and objective function.Bons et al.52suggested that physics analysis of high-fidelity can attenuate the multimodality in the design space.Our work focuses on the optimization framework utilizingsurrogatemodelsand the optimization is performed on the surrogate model instead of the real relationship between the airfoil shapes and the aerodynamics as in these previous works.Therefore,the inaccuracy of the surrogate can also lead to high possibility of the multimodality of this optimization problem as the limited number of initial training samples cannot guarantee the unimodality of the surrogate model.In this case,the optimum found at each optimization iteration is added into the training samples to increase the accuracy of the surrogate model in our framework.In light of the multimodality of the surrogate model,a robust optimization framework should help to obtain a fast and steady convergence of this optimization problem.Therefore,the purpose of this paper is to demonstrate the stability of the proposed optimization framework.In addition to that,different shape representation methods and the size of the searching space may also affect the number of local optima.That is to say,the possibility of multimodality in the airfoil design space depends on the specific way to solve the problem,where there is no theoretical proof so far.
In conclusion,our optimization framework provides significant improvement in the robustness and the efficiency of the convergence compared to the traditional GA-based approach,which implies its promising potential in handling more complex aeronautical problems.
Acknowledgements
This study was co-supported by the Aeronautical Science Foundation of China(Nos.20151452021 and 20152752033),the National Natural Science Foundation of China(No.61300159),theNaturalScienceFoundation ofJiangsu Province of China(No.BK20130808),and China Postdoctoral Science Foundation(No.2015M571751).
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Particle image velocimetry for combustion measurements:Applications and developments
- Abnormal changes of dynamic derivatives at low reduced frequencies
- Experimental study of an anti-icing method over an airfoil based on pulsed dielectric barrier discharge plasma
- Envelope protection for aircraft encountering upset condition based on dynamic envelope enlargement
- Effects of the radial blade loading distribution and B parameter on the type of flow instability in a low-speed axial compressor
- Adaptive sliding mode control for limit protection of aircraft engines
