Energy based 3D trajectory tracking control of quadrotors with model-free based on-line disturbance compensation

Ysser BOUZID,Houri SIGUERDIDJANE,Ysmin BESTAOUI

aIBISC Laboratory,Universite´d’Evry Val d’Essonne,Universite´Paris-Saclay,Evry 91020,France

bL2S,CentraleSupe´lec,Universite´Paris-Saclay,Gif sur Yvette 91192,France

KEYWORDS IDA-PBC;Model-free control;Nonlinear flight control;Robust control;Trajectory tracking

Abstract In this work,a Revisited form of the so-called Model-Free Control(R-MFC)is derived.Herein,the MFC principle is employed to deal with the unknown part of a plant only(i.e.,unmodeled dynamics,disturbances,etc.)and occurs beside an Interconnection and Damping Assignment-Passivity Based Control(IDA-PBC)strategy.Using the proposed formulation,it is shown that we can significantly improve the performance of the control through the reshaping properties of the IDA-PBC technique.Moreover,the control robustness level is increased via a compensation of the time-varying disturbances and the unmodeled system dynamics.This on-line compensation capability is provided by the MFC principle.The problem is studied in the case of Multi-Input Multi-Output(MIMO)mechanical systems with an explicit application to a small Vertical Take-Off and Landing(VTOL)Unmanned Aerial Vehicle(UAV)where a stability analysis is also provided.Numerical simulations have shown satisfactory results,in comparison with some other control strategies,where an in-depth discussion with respect to the control performance is highlighted by considering several scenarios and using several metrics.

1.Introduction

Vertical Take-Off and Landing(VTOL)Unmanned Aerial Vehicles(UAVs)are very popular platforms of research,due to their maneuverability,hovering ability,and maintenance and construction simplicity.In Refs.1,2,hexacoptors are used to build binocular vision based UAVs.A novel forestfire detection method using quadrotor motion features is detailed in Ref.3Moreover,quadrotors are considered as a good case study to design,analyze,and implement flightcontrol strategies.

It is necessary to design a controller so that a quadrotor will be able to efficiently follow a predefined trajectory,particularly in the presence of disturbances.For this reason,many studies have led to the development of sophisticated and robust nonlinear control laws.In Ref.4,anH∞controller and backstepping approaches were proposed in order to stabilize the attitude and tackle the path-tracking problem of a quadrotor,respectively.The authors in Ref.5proceeded by considering two subsystems and applying two nested control strategies.The Internal Model Control(IMC)strategy was applied to the inner loop whilst the Immersion and Invariance(I&I)one was applied to the outer loop.In Ref.6,a robust adaptive control was proposed for attitude stabilization under external disturbances and validated by real-time implementation.Refs.7,8presented a sliding mode control combined with the backstepping technique for the sake of stabilization,regulation,and trajectory tracking.Other approaches have been applied for an instance direct adaptive sliding mode controller9and an SMC-neural networks controller.10

However,some of the existing control strategies require an accurate modeling of a system in order to perform a good control,which is extremely difficult especially when the system is maneuvering in harsh environment.This is due to the lack of complete knowledge on the system and its surrounding phenomena.In this regards,a Model-Free control(MFC)technique has been developed(see for instance11).The main advantage of this control strategy is that it doesn’t require the knowledge of system dynamics as it involves a continuous updating of the input–output of a very-local model.This anticipation property makes a control possible even with the presence of disturbances.It has been employed in many real cases such as a mobile robot11and quadrotors.12

In a certain point of view,assuming no available model is not totally a correct assumption due to the fact that most of systems,at least,may be approximated by mathematical models even with poorly known dynamics.Therefore,using available information about a system will bring a notable benefit and significantly improve the performance of control.In such a case,a nonlinear control auxiliary input should be used to deal with the nonlinear modeled dynamics of the system.Notice that the classic MFC control employs a PID controller as an auxiliary input.As in general,the tuning of PID parameters allows to meet the desired specifications of control,we propose the use of a reference model based nonlinear control technique that achieves a control with required specifications,by means of Interconnection and Damping Assignment-Passivity Based Control(IDA-PBC).

Quadrotors allow the development of advanced manipulation tasks(robot vision13, flying sensors14,etc.)where damping and inertial properties play a significant role.For this reason,the development of techniques that explicitly present these factors is of major impact.Therefore,in the last two decades,the use of the so-called Port-Controlled Hamiltonian(PCH)representation has attracted the attentions of researchers.Many control tools have been developed to deal with this compact representation.Passivity-Based Control(PBC)is well known especially in mechanical applications for controlling nonlinear systems.An improvement was developed through Interconnection and Damping Assignment(IDA)where the use of energy shaping was originated in Ref.15Recently,the IDA-PBC has become an efficient tool in nonlinear control applications(electrical,hydraulic,chemical,and mechanical)and has been illustrated in several real experimentations including electrical motors16,robots with a parallel architecture17,rotary inverted pendulum18,etc.

1.1.Contribution

As stated above,the classic MFC is data-driven,i.e.,only input and output data are used while the differential equations associated to the mathematical physical laws are ignored.Therefore,the MFC does not distinguish between system dynamics and disturbances.

Since control requires some mapping,taking system information,a controller is constructed in this paper through the use of the MFC principle to accommodate the unknown parts of a system and disturbances whilst an auxiliary input is used to ensure the asymptotic convergence of tracking errors toward the origin.Therefore,this paper involves the MFC algorithm,which requires only system measurements(not a system model)to deal with uncertainties and disturbances in order to ensure a good level of robustness.

In the literature,the use of MFC is always linked to a linear PID controller.Unlike this common case,this paper proposes an IDA-PBC approach to design the auxiliary input that enables the system to meet the desired specification of control.

This formulation is considered as a Revisited form of the classic Model-Free Control(R-MFC)strategy that combines both MFC and IDA-PBC approaches.Such an approach has potential advantages in control performance as well as its robustness level compared to classical controllers.This is due to the capability of MFC in estimating system uncertainties,modeling errors,and disturbances as well as the IDAPBC’s capability in meeting a fixed control performance.

Byusingthisformulation,theasymptoticstabilityofthesystemisguaranteed,forwhichadetailedanalysisisprovidedhereafter.It is applied to a small quadrotor where numerical simulations are also provided.Throughout this paper,a performance assessment is presented via results of several scenarios with complementary comments on the proposed revisited strategy of control with respect to other techniques(MFC and backstepping approaches).Particular attention is paid to the tracking accuracy and energy consumption of each control strategyconsideringsomeperformancecriteria,suchasIntegral Squared Error(ISE)and Integral Squared Control Input(ISCI).

1.2.Outlines

The remainder of this paper is organized as follows.In Section 2,some notations and concepts of energy based control are brie fly recalled.Section 3 concerns the dynamics of a VTOL quadrotor and the control architecture.Sections 4 and 5 introduce the design of our nonlinear control approach.Simulation results are illustrated in Section 6.Finally,the paper is ended with some concluding remarks.

2.Background

2.1.Notations

We denote R，Rn,and Rn×nthe sets of real numbers,vectors,and matrices,respectively,and R+denotes the non-negative real numbers.For an arbitrary real variablex,Dxdenotes the set of allowable values（x∈Dx）whereDxmay belong to R，Rn,or Rn×n.In×n∈ Rn×nis the square identity matrix with a dimension ofn×n.The notation ATdenotes the transpose of matrix A.The spectrum eig（A）is the set of eigenvalues of square matrix A ∈ Rn×n.xmaxandxmindenote the maximal and minimal values of scalarx,respectively.A functionf（x）is said to be of classC1if the first derivativewith respect toxexists and is continuous.The operatordenotes the first time derivative of□,and□（n）is itsnth time derivative.sat（x）denotes the saturation function for variablex,which is defined as

2.2.Definitions

In this section,we brie fly recall some important concepts that are needed to facilitate the understanding of the procedure given hereafter.

2.2.1.Port-Controlled Hamiltonian models

Brie fly,we will describe the modeling of systems via the Hamiltonian equations that appeared in 1994.Deeper investigations may be found,for instance in Ref.19

Definition 1.Every system having the representation

where x ∈DxRndenotes the state vector,H（x）:Dx⊆Rn→R is aC1function that represents the internal energy accumulation in the system;J（x）is the interconnection skew symmetric matrix,R（x）≥ 0 is the damping symmetric matrix,g（x）is the input matrix,u ∈ Rpis the input vector and y is the output,is called a PCH system.

This representation explicitly shows the physical properties of a system through interconnection and damping matrices and the internal energy,which makes its use particularly suitable for mechanical,electromechanical,and electrical systems.

2.2.2.Passive systems

In theliterature,passivesystemsmayhavenumerous definitions.We state the following one.

Definition 2.19Let the system

with u ∈ Rp,x ∈Dx⊆Rn，g（x）:Rn→ Rn×pthe input matrix,ythe output,x*∈Dxso that f（x*）=0 is an equilibrium point,and also h（x*）=0,be a passive system if there is a continuous storagefunctionH:Dx→ R+withH（x*）=0,so that∀t≥t0∈ R+and ∀u

2.2.3.Detectability

A system is detectable from a given output if all states that cannot be observed decay to zero asymptotically(see the work of Byrnes et al.20for more details).

2.3.Review on MFC

The model-free approach does not require prior knowledge of system parametersand characteristicswherethewhole dynamic and even external disturbances are approximated by an ultra-local differential relation of order ν valid only on a very short time period δTgiven by

whereyis the system output,Frepresents the system dynamic,uis the control input,and β is a scale parameter.

The dynamicF（t）at instanttcan be computed directly using the captured outputy（t-1）and the last applied control inputu（t-δT）as

The next control inputu（t）to apply at timetis computed from the estimation）as

whereyr（t）is the reference trajectory,e=yr-yis the tracking error,andv（t）denotes the auxiliary input.v（t）is designed according the order ν to be a P,PD,or PID controller(for more details,the reader may refer to the work of Wang et al.12).

3.Quadrotor modeling&control architecture

From the fundamental principle of dynamics,we model a quadrotor as a rigid body for the validation of control performance,neglecting some aerodynamic effects such as gyroscopic and ground effects.The system operates in two coordinate frames:the Earth fixed frameR0（O，X，Y，Z）and the body fixed frameR1（O1，X1，Y1，Z1）(see Fig.1).

Let η= ［φ，θ，Ψ］Tdescribe the orientation of an aerial vehicle(roll,pitch,yaw),and χ = ［x，y，z］Tdenotes its absolute position.In this study,we consider a simplified dynamic model of the vehicle that is derived in our previous work21in order to make the controller implementation simpler and easier and furthermore to show the efficiency of our control strategy that can deal with the unmodeled and neglected dynamics.The considered mathematical model may be written under the general mechanical equation as follows:

Fig.1 Frame representation.

where q= ［χ，η］T∈Dχ×Dη⊆R3×R3is the generalized coordinates,is composed of the mass, M=mI3×3, and the inertia matrix,denotestheCoriolisterm,G ∈ R6= ［0，0，mg，0，0，0］Tdenotes the gravitational term,B（q）=I6×6is the input matrix with

in whichmis the mass,gthe gravity acceleration,u1the total thrust of four rotors,τ= ［u2，u3，u4］Tthe control torque vector,ands（.）andc（.）abbreviations for sin（.）and cos（.）,respectively.The parameters of UAV system are displayed in Table 1.

Our control is designed to ensure tracking of the desired trajectory along the three axes(xr,yr,zr)and the yaw angle Ψr.These reference trajectories are provided on-line by a Trajectory Generator Block(TGB).The controller is based on a decomposition into two sub-systems.The first one is related to the position control while the second one is related to the attitude stabilization.Having two sub-systems in cascade with different dynamics is not an easy control problem especially in conditions of under-actuation.In order to simplify the design of the controller,we consider thatxandyare controlled through two virtual inputsuxanduythat drive the system to reachxrandyr. These two virtual inputs are given as

Then,from Eq.(10),we can calculate the desired roll and pitch trajectories as follows:

It is worthwhile to mention that the VTOL vehicle does not have any mechanical singularity.However,the considered model has some mathematical singularities,namely,φ=and θ = .These singularities are not reached due to the fact that no aggressive maneuvers are considered within this paper.However,in order to ensure that the reference angles given bythe following equality must be verified:

In other words,uxanduymust be saturated.Therefore,Eq.(11)becomes

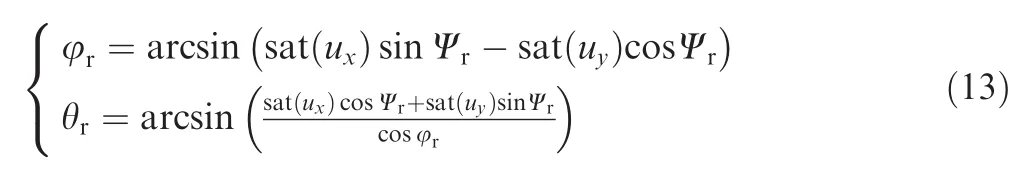
The reference angles,φrand θr,are considered as inputs for the rotation subsystem.The altitude is controlled byu1whereas the roll,pitch,and yaw angles are controlled by（u2，u3，u4）,respectively.The control structure scheme is shown in Fig.2.

4.R-MFC flight controller design

The classic MFC approach proceeds by considering an ultralocal model,valid in a short time interval that approximates the nonlinear model via input–output behaviors using available experimental data without any modeling step.However,this online numerical differentiator and estimation may fail with some highly nonlinear and/or time-varying dynamics that need to be carefully treated.In addition,most systems have a mathematical model even if it is not accurate.Note also that the MFC does not distinguish between model mismatches and perturbations.Therefore,to be more realistic,our approach employs the model-free principle to only deal with the unknown part of the controlled system where the use of the known part brings more benefits and makes the control more efficient.

This proposed formulation that we can denote by the acronym R-MFC is explained through a class of systems written under the general mechanical equation.This class of systems is widely adopted in the robotics and mechanical fields.Motivated by Eq.(4)and for the sake of clarity,Eq.(7)is written under a compact form considering the general case as

with

Fig.2 Quadrotor control architecture.

where q∈Dq⊆Rnis the output vector,u∈Rndenotes the input vector,M=MT∈ Rn×n＞ 0 is the inertia matrix,C）∈Rn×ndenotes the Coriolis term,G∈Rndenotes the gravitational term,and B（q）∈ Rn×ndenotes the input matrix.

Remark 1.Notice that Eqs.(4)and(14)have the same form.However,the former one is with unknown dynamics whilst the latter one is fully known.

Usually,Eq.(14)is quite simplified with neglected and unmodeled dynamics.Moreover,the execution of trajectories can be easily affected by external disturbances,which introduces some unknown terms.Therefore,a term δF could be added to nominal Eq.(14)gathering the neglected and unmodeled dynamics and the external disturbances.Obviously,an additional effort δu is requested to deal with this new term δF.From Eq.(4),we take δu= κu.Thus,the input–output relationship of the anticipated model may be represented by the following system:

where κ ∈ Rn×nis a positive definite diagonal scale matrix fixed by the user,and δF ∈ Rnis an estimated term.In fact,an order ν=2 of Eq.(15)is chosen according to the prior knowledge of the system.It equals to the order of mathematical Eq.(14).

Remark 2.For the classic MFC technique,vis fixed by the user and may equal to 1 or 2.

Therefore,the difference between Eqs.(14)and(15)lies in the presence of the unknown modeled part δF that can be estimated at each instanttas

As the past input vector u（t- δT）in the previous time interval and the 2{nd}derivative of the measured output vector q（t- δT）are known,the value ofis computed.This estimation is valid for a short period δTonly and should be continuously updated at every iteration of the closed-loop controller.

Obviously,the estimate of the second-order derivative（t- δT）yields an estimate ofHowever,output signals such as orientation velocities are often noisy.Many significant advances on the numerical differentiation of noisy signals are elaborated in the literature.

where the matrix B（q）+κ is non-singular inDq.uC（t）=（t）plays the role of compensator of the unknown part,and ua（t）is consideredasanauxiliaryinputthatensuresanasymptoticconvergenceofthetrackingerrorsoftheclosedloopintotheorigin.Injecting the input of Eq.(17)into Eq.(15)leads to a new and fully known nonlinear model eliminating the unknown part as

The classic MFC technique employs,in the case of ν=2,a PID controller as an auxiliary input:

that leads to an intelligent PID where E=q-qris the tracking error vector and qris the reference trajectory vector.KP，KI,andKDdenote the usual tuning gains.However,the PID controller cannot deal with the nonlinear term Fin other operation points rather than the equilibrium point.Herein,we proceed with a different way by employing a sophisticated tool rather than the PID structure where the main goal is to ensure an asymptotic convergence,towards the origin,of the tracking errors of the closed loop of Eq.(18).In this stage,a broad range of control strategies can be applied.

The use of PID,in the classic form of MFC,allows to ensure a given performance of the system time response according to given specifications(overshoot,settling time,accuracy,etc.)via the tuning of control parameters.To achieve the desired specifications,using another control procedure is more challenging.Therefore,we employ a reference model based control strategy where the control specifications are a priorifixed.Then,the control input pushes the system to follow the same behavior as that of the target model.

5.IDA-PBC based auxiliary input

In the following,trajectory tracking control is achieved using the IDA-PBC approach.In this technique,we modify the total energy function of Eq.(18)to assign the desired equilibrium and damping injection matrix to meet the asymptotic stability.To preserve the energy interpretation,the closed-loop system ispresented in a Port-Controlled Hamiltonian (PCH)representation.

5.1.System energy and PCH model

Explicitly,Eq.(18)is written as

The system’s Hamiltonian energy,H（q，p）,that equals to the sum of the kinetic energy,T（q，p）,and the potential one,V（q）,is written as

Therefore,

where p∈Rnis the generalized momentum.

This system has a natural stable equilibrium configuration.This latter one is related to the minimum of energy.A PCH model is needed in order to design a controller based on the IDA-PBC methodology.From Eq.(20),the PCH representation can be written as

with

where J （q，p）is the interconnection skew symmetric matrix and R（q，p）is the damping symmetric matrix.

Remark 3.Obviously,from Eqs.(22)and(23),=M-1p.This relationship also holds for the closed-loop system.

Proposition 1.Eq.(23)is passive if it is detectable from the output y=MT▽pH（q，p）.

Proof.Differentiating Eq.(22)along the trajectories of Eq.(23)leads to

Introducing the last row of Eq.(23)into Eq.(25),we obtain

Doing some computations,leads to a simplified equation as

If the system is detectable from the output,i.e.

and by integration,Eq.(26)becomes

Therefore,the passivity property is satisfied(see Definition 2),i.e.,

5.2.Target dynamics

Motivated by Eq.(21),we propose a desired energy function as

We modify the total internal energy function of the closedloop system to assign the desired equilibrium configuration and we require thatHd（q，p）will have a minimum at （q*，p*）,thus

whereVd（q）and Md=＞ 0 represent the desired closedloop potential energy function and inertia matrix,respectively,with

Remark 4.Our objective beyond this controller design is to ensure stabilization as well as tracking of any reference trajectory.Therefore,we take the reference trajectories as the desired equilibrium configuration. In other words,（q*，p*）= （qr，pr）.

To preserve the energy interpretation,we also require the desired closed-loop system to be in a PCH form as

where Jd（q，p）is the desired interconnection matrix and Rd（q，p）is the desired damping matrix.For a PCH representation,the interconnection matrix has to be skew symmetric while the damping matrix is symmetric(see Definition 1).From Eq.(24)and for the sake of simplification,we define Jdas

Rdinjects a damping into the system via the passive output of Proposition 1(more details are provided hereafter).Therefore,Rdis selected to be

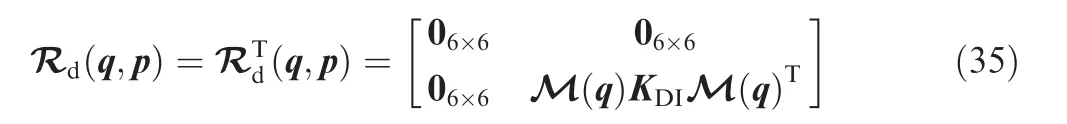
J（q，p）is a skew symmetric matrix and KDI=＞0 contains the control parameters. Obviously, the matrix［Jd（q，p）-Rd（q，p）］has the same form as that of the original system.

5.3.Energy shaping&damping injection

Commonly,the control input of PBC is composed of two terms22as follows:

where uDIacts on damping and uESis designed for energy shaping.

The controller is obtained by substituting Eq.(36)into Eq.(23)and making the resulting equations equal to Eq.(33).Thus,

Rdinjects a damping into the system via a negative feedback of the passive output selected in our case as MT▽pHd(see Proposition 1).The damping injection term is then

Thus,the second row leads to the energy shaping as

Finally,the R-MFC is split into three parts as

where uCdeals with the unknown parts and allows to maintain a certain level of robustness,uESallows to meet the desired specification through the target model components,and finally the damping injection term uDIis to guarantee a damped response.Our approach is summarized in Fig.3.

5.4.Control design for quadrotor and stability analysis

We would need to resolve the partial differential equation(PDE)of Eq.(39)for the unknown MdandVd.Then for the sake of simplification,we keep the interconnection matrix unchanged,namely,Md=M and J=0,so uESbecomes

Therefore,

whereVdis an arbitrary function of χ and η.From Eq.(32),the necessary condition,▽qVd（q*）=0,and the sufficient condition,Vd（q*）＞ 0,will hold at q*.Vdhas its minimum at q*=qr(see Remark 4).In our case,we chooseVd（q）to be a quadratic function,which leads to

Fig.3 R-MFC scheme.

where KESχand KESηdenote the positive definite matrices of the control parameters.

Now,the auxiliary input for the quadrotor is given by

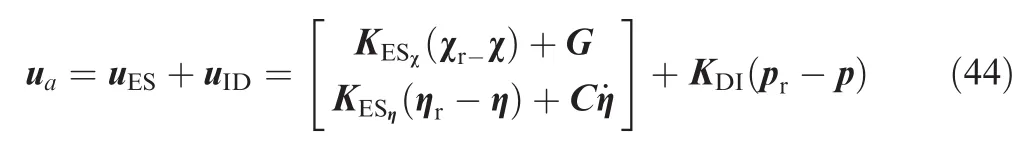
The stability of the closed-loop dynamics of the quadrotor system in Eq.(18)is introduced by the following theorem.

Theorem 1.The closed-loop system inEq.(18)written under a PCH form,using the control law inEq.(44),is asymptotically stable.

Proof.Following the IDA-PBC approach described above,the closed-loop system in Eq.(18)written under the PCH model in Eq.(23)is equivalent to the desired PCH model in Eq.(33)using the control law in Eq.(44).Hd（q，p）is a positive definite function chosen herein as a Lyapunov candidate function where the first time derivative is

Therefore,the closed-loop system in Eq.(18)is asymptotically stable.□

6.Results and discussion

In this section,we test the effectiveness of the proposed controller not only in an ideal case but also in the presence of different disturbances.For a significant analysis of the features of the proposed controller,two additional nonlinear controllers are considered.The first one is the classic model-free technique that exhibits promising results(for details,one may refer to the work of Wang et al.12)whilst the second one is traditionally applied for quadrotors,i.e.,the BackStepping(BS)approach.For a fair comparison,we follow the same protocol andfit the same conditions.The control parameters of the overall strategies are tuned using Genetic Algorithms(GAs)in the ideal case,and then kept for the entire proposed scenarios,for which the objective is to reduce the steady-state errors.Thus,the fitness function is given by

wheretiandtfdenote the initial and final instants of optimization,respectively.The obtained control parameters for the RMFC are depicted in Table 2.Those of backstepping are given in Table 3(see Appendix A).

The overall system dynamics and control laws are implemented using the Matlab tool.The total simulation time is40 s,and the sampling time is set to 0.01 s.We simulate the response of the quadrotor using the available parameters of an AR-Drone(see Table 1).The following scenarios are proposed.

Table 2 R-MFC control parameters.

Table 3 Backstepping control parameters.

(1)Basic scenario:In this scenario,after the take-off,the quadrotor tracks a square reference trajectory（2 m × 2 m）.At each corner,the quadrotor hovers for five seconds,and thenflies to the next corner,where the flight duration between two corners is fixed at T=5 s.Therefore,this trajectory may be described as

WithT=5 s,tf=40 s,andLr=2 m.xr= σ（t））with t1=5，t2=t1+T，t3=25，t4=t3+T yr= σ（t）with t1=10，t2=t1+T，t3=30，t4=t3+T zr= σ（t））witht1=0，t2=t1+T，t3=35，t4=t3+T

(2)Parameters uncertainties:The control systems should be capable of tolerating model or parameter uncertainties.We suppose that the inertia matrix elements and the aerodynamic coefficients are underrated by 50%of the real values.

(3)Extra payload:The flight controllers should be able to ensure a good performance with a good level of robustness even with an extra mass.Therefore,in this scenario,the quadrotor is supposed carrying a heavy camera with an additional mass that represents 50%of the initial mass of the quadrotor.The camera is modeled as a rigid compact body located at the center of mass of the quadrotor.

(4)Sensor noise:Low-cost sensors are usually used in quadrotors.Thus,the precision is low and output signals are always noisy.Moreover,estimation algorithms also causebigerrorsanddrifts.Inthisscenario,wetestthetolerance of controllers to noise that may affect the measured signals.Thus,we add the sensor noise on the states of the system.The expression of the noisy states is

where rand（·）is a Matlab function,which generates a random number between 0 and 1.Ncis a scale parameter to adjust the level of noise.

(5)Wind disturbance:Quadrotors are readily affected by external disturbances during outdoor flights.This scenario is dedicated to test the stability of control systems while encountering environmental disturbances,namely,gust of wind.Here,we accept that the wind causes the same acceleration intensity on all x，y，z-axes.These accelerations are considered as perturbations added to the equations related to the forces in the quadrotor model.Therefore,the disturbed model may be expressed as follows:

The profile of this acceleration is depicted in Fig.4 and expressed explicitly as

witht1=10 andt2=30，i=x，y，z.

First of all,we start with the basic scenario.We plot separately,the attitude angles in Fig.5,the tracking errors of the translations along thex,y,z-axes in Fig.6,and the control inputs in Fig.7.

Fig.4 Wind disturbance estimation.

Fig.5 Attitude angles.

Overall,from the curves illustrated in Figs.5–7,the controllers can correctly stabilize the roll,pitch,and yaw angles when the quadrotor follows its reference trajectory with small errors and moderate energy consumption.From Fig.6,we observe that R-MFC ensures a damped response with a less overshoot compared to the other considered techniques,which is a significant result,due to the fact that a large overshoot leads to physical oscillations of a vehicle and engenders overturns of nearby constraints.

Obviously,the previous curves are not able to show the differences between the controllers because all the techniques exhibit acceptable results in the ideal case.Therefore,we suggest quantifying the obtained results in order to get a close view on the features for deep analysis of the performance.Some analytical tools are considered,such as:

(A)Integral Square Error (ISE): It is given by

(B)Integral Squared Control Input(ISCI):It allows to measure the consumed energy using ISCI=

The quantified metrics are summarized for each scenario in Table 4.

Fig.6 Tracking errors along the three axes.

Overall,as shown in Table 4,the three controllers exhibit an acceptable behavior with moderate consumed energy regardless the external effect.Nonetheless,the extra payload as the gust of wind requests additional thrust in order to ensure good performance.

One may notice that,from Table 4 and for the basic scenario,the BS technique is the less accurate technique(ISE=0.152)followed bytheclassicMFC technique(ISE=0.088),while the R-MFC is the most accurate one(ISE=0.0425).We also observe that the MFC consumes more energy while the R-MFC consumes less energy.

The accuracy of control degrades less or more for the BS according to the disturbance nature.However,the accuracy is almost the same when using the MFC or R-MFC,which demonstrates the efficiency of the online estimation of the disturbance.It is then worthwhile to note that the MFC as well as the R-MFC are not sensitive to the disturbances where the thrust is requested according to the disturbance intensity in order to keep the same performance.

Finally,among the considered approaches,the R-MFC exhibits the best performance in terms of accuracy and damped response with an acceptable level of energy consumption.Using our R-MFC is more relevant,because that allows estimating the disturbances that affect our system such as the wind,unlike the classic MFC that cannot distinguish the disturbances from the system dynamics.This is justified by Fig.4 that shows the estimated wind using our R-MFC principle.

Fig.7 Control inputs.

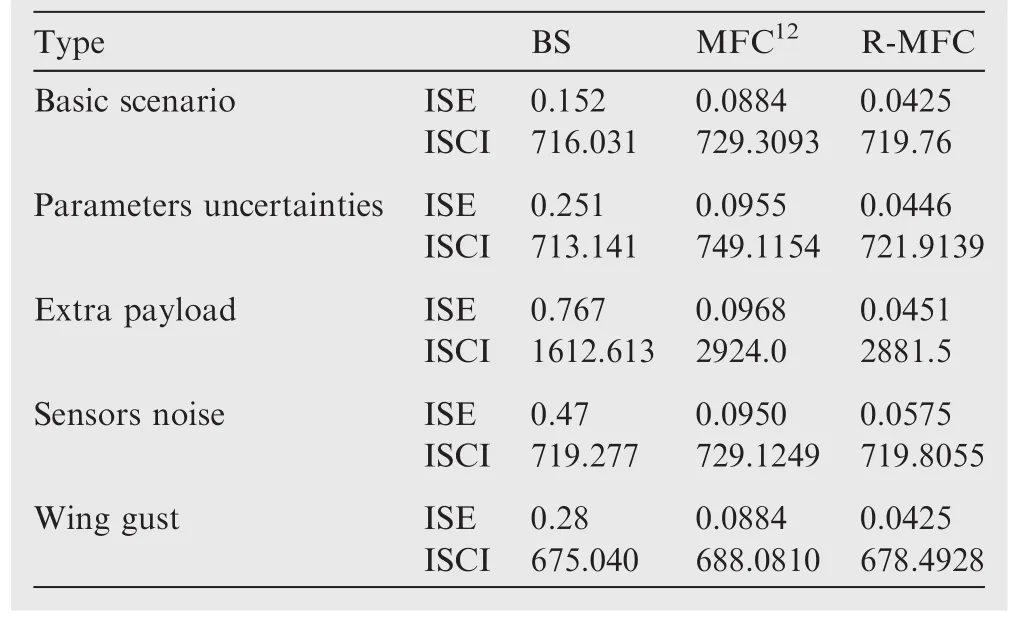
Table 4 Quantified metrics for each scenario.

7.Conclusions

In this paper,a reformulation of the actual MFC controller is described.It uses an auxiliary input,and by bringing some changes(see Sections 4 and 5),it operates in a closed-loop form.It improves the performance with respect to structured and unstructured uncertainties.Numerical simulations have been performed using the non-linear dynamic model of a quadrotor in order to test the effectiveness of the designed controller.The good efficiency of our approach is demonstrated in multiple test scenarios.The settling time is shown to be quite fast with good accuracy,and a high level of robustness is ensured with respect to parameters uncertainties or external disturbances.The autonomous vehicle exhibits good performance under wind gust and maintains its defined position very well.It is worthwhile to stress that our strategy is also able to estimate disturbances.

Appendix A

The control laws,for backstepping,considered in the comparison are listed below:

wheree（.）= （.）r- （.）denotes the tracking error between the state and its reference trajectory （.）r,ands（.）is a surface defined bys（.）=˙e（.）+k0（.）e（.）.The control parameters for the backstepping approach are displayed in Table 4.