Evaluation of mixed mode-I/II criteria for fatigue crack propagation using experiments and modeling

Oğuzhn DEMIR,Ali O.AYHAN,Sedt IRIC,Hu¨seyin LEKESIZ

aDepartment of Mechanical Engineering,Sakarya University,Sakarya 54187,Turkey

bDepartment of Mechanical Engineering,Bilecik S■eyh Edebali University,Bilecik 11210,Turkey

cDepartment of Mechanical Engineering,Bursa Technical University,Bursa 16310,Turkey

KEYWORDS Crack propagation;Fatigue crack growth simulation;Fatigue crack growth test;Fracture mechanics;Mixed mode-I/II

Abstract In this study,in-plane mixed mode-I/II fatigue crack growth simulations and experiments are performed for the Al 7075-T651 aluminum alloy which is widely used in the aerospace industry.Tests are carried out under different mode mixity ratios to evaluate the applicability of a fracture criterion developed in a previous study to mixed mode-I/II fatigue crack growth tests.Results obtained from the analyses and experiments are compared with existing and developed criteria in terms of crack growth lives.Compact Tension Shear(CTS)specimens,which enable mixed mode loading with loading devices under different loading angles,are used in the simulations and experiments.In an effort to model and simulate the actual conditions in the experiments,crack surfaces of fractured specimens are scanned,crack paths are modeled exactly,and contacts are defined between the contact surfaces of a specimen and the loading device for each crack propagation step in the analyses.Having computed the mixed mode stress intensity factors from the numerical analyses,propagation life cycles are predicted by existing and the developed mixed mode-I/II criteria and then compared with experimental results.

1.Introduction

Fracture mechanics and its applications,including mixedmode fracture,are being studied extensively in such important areas as energy,defense,aviation,and space industries in developed countries that produce high-technology products.Fracture and crack propagation analyses are performed for airframe,helicopter,and aircraft engine parts even during the design phase.Many of the fracture and fatigue crack propagation problems that have been encountered in the aviation industry are related to fuselage of military and passenger aircraft,gas turbine engines and turbine blades.1–13

Fatigue crack growth studies for many practical engineering problems have mostly concentrated on pure mode-I loading condition over the past six decades.Unfortunately,pure mode-I loading condition does not always occur in practice,and in many cases,cracks are exposed to mixed mode loads,i.e.,directions of the loads are not normal to the crack plane.During crack growth under mixed mode loading,crack growth direction changes in accordance with mode mixity ratios.Thus,for accurate assessment of life predictions,crack growth direction plays a key role along with the fatigue crack growth rate under mixed mode loading conditions.Mixed mode fracture and crack propagation problems are encountered due to different reasons:multi-axial and mixed mode loads,nonperpendicular orientations of crack surfaces with respect to global uniaxial loading,and different types and combinations of boundary conditions.

Several stress-or energy-based fracture criteria have been proposed so far to understand the fracture mechanism of inplane mixed mode problems.Maximum Tangential Stress(MTS),14minimum Strain Energy Density(SED),15Maximum Energy Release Rate(MERR)16,17and Maximum Tangential Strain(MTSN)18criteria are some of the most common theoretical criteria used in fracture and crack propagation analyses for mixed mode-I/II fracture problems.Tanaka,19Richard20–22and Pook23et al.also proposed different fracture criteria by defining equivalent Stress Intensity Factor(SIF)equations.For predictions of the crack growth increment and direction under in-plane mixed mode loading,definition of an equivalent SIF representing a combination of mode-I and mode-II SIFs is essential.Although many criteria have been proposed with regard to predictions of crack growth increment and its direction for mixed mode-I/II fracture problems,there is no standard criterion for mixed mode crack growth tests.Biner24investigated the crack growth behavior of AISI-304 stainless steel under mixed mode-I/II loading conditions by using Compact Tension Shear(CTS)specimens,and compared experimental crack growth directions with those obtained using the SED criterion and the MERR criterion.The author reported that the SED criterion significantly over-estimates the de flection angle of crack growth at high mode mixities.Zafosnik et al.25also performed mixed mode-I/II crack growth simulations and tests using CTS specimens made of Al alloy and results obtained from simulations combined with MTS and SED criteria were compared with experimental data.The results showed that,as is the case with Biner’s results,the SED criterion is less accurate for determination of the kink angle under high mode mixities,and the MTS criterion provides good prediction agreement,but for further crack extensionsthecriterion deviatesfrom experimentaldata.A literature survey about various criteria proposed for predictions of mixed mode crack growth directions and rates was given by Qian and Fatemi.26They reported by referring to studies existing in the literature that significant discrepancies occur between crack growth criteria when the mode-II component is dominant under mixed mode-I/II loading conditions.Ren et al.27reviewed several widely accepted fracture criteria in terms of crack initiation angle and fracture toughness ratio under in-plane mixed mode fracture.The authors indicated that many criteria can provide a good prediction for predominately mode-I fractures,but none of them yields good predictions under predominately mode-II conditions.In a previous paper,28mixed mode-I/II fracture analyses and experiments were performed for different types of CTS specimen,and data obtained from the experiments was compared with predictions from the analyses using existing criteria in the literature.Results showed that existing criteria yield reasonably close predictions to those of experiments for up to moderate levels of mode mixity in the loading.However,most existing criteria start deviating from experimental measurements for highly mixed mode loading conditions.Therefore,using all data obtained from analyses and experiments,improved empirical mixed mode-I/II fracture criteria were proposed in terms of fracture loads and crack de flection angles,and the developed criteria28were validated by applying them to the results of the experiments.Although the previous study28focused on mixed-mode fracture toughness tests under static loading,in this study,fatigue crack growth modeling and experiments are performed to validate the developed equivalent SIF equation in terms of propagation life cycles.In this context,inplane mixed mode-I/II fatigue crack growth experiments are performed by using CTS specimens.Fracture surfaces of broken specimens are modeled exactly by scanning the surfaces,and fracture analyses are performed by simulating the real conditions in the experiments for all crack growth increments of the tests.Having computed the mixed mode stress intensity factors from the numerical analyses,equivalent SIFs on the crack fronts are calculated using existing and developed criteria,and life cycles are computed for each criteria.Finally,crack growth lives under different loading angles(30°,45°,60°and 75°)are compared with experimental results.

2.Existing in-plane mixed mode criteria

For determination of fracture behaviors under in-plane mixed mode loading conditions,there are various criteria that exist in the literature.Some of these criteria are summarized in this section.

The Erdogan and Sih criterion14is one of the most commonly used criterion for in-plane mixed mode problems.According to this criterion,crack propagates from the crack tip radially at a direction which contains the maximum tangential stress.If this tangential stress exceeds a critical value or an equivalent stress intensity factor(Keq)reaches the fracture toughness(KIC)value of the material,crack propagation becomes unstable,and fracture occurs.Keqand the crack de flection angle for this criterion are expressed by

whereKIandKIIare the SIFs of mode-I and mode-II,respectively;φ0is the crack de flection angle.

Another criterion developed for mixed mode-I/II problems is the Richard criterion.21,22The equivalent SIF and crack de flection angle can be determined by the following equations:

In Eq.(3),α1is a material parameter describing the ratio ofKIC/KIICand generally taken as 1.155.

Another criterion was proposed by Tanaka,19who stated a concept of the equivalent SIF for mixed mode conditions.According to this criterion,the equivalent SIF is formulated by

Pook23also developed an in-plane mixed mode criterion and proposed an equation from which the equivalent SIF can be obtained using mode-I and mode-II SIFs as

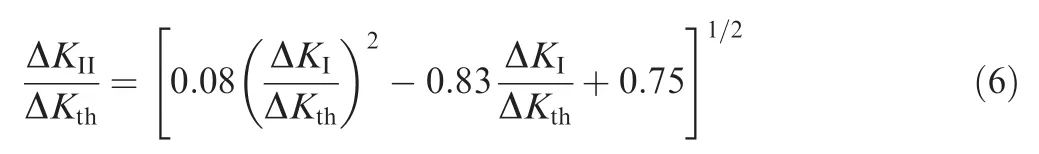
where ΔKthis the threshold range of stress intensity for mode-I.

In a previous study,28modeling and analysis of in-plane mixed mode-I/II fatigue crack growth experiments were carried out for each mode mixity ratio to evaluate the applicability of the equivalent SIF criterion developed for mixed mode-I/II fracture problems.The equivalent SIF equation with regard to the developed criterion28obtained using two types of specimens,namely CTS specimen and T-specimen,is given by

3.Fatigue crack growth experiments

In this section,fatigue crack growth experiments are performed by using Compact Tension(CT)specimens under pure mode-I loading and by using CTS specimens under in-plane mixed mode loading.The Al 7075-T651 aluminum material,which has an elastic modulus of 70 GPa,a Poisson’s ratio of 0.33,and an initial yield stress of 460 MPa,is machined from rolled plates in the L-T rolling direction and used for all experiments.Before fatigue crack growth experiments,fatigue precracking is performed under mode-I loading according to the ASTM E647-13a standard29by using an axial fatigue test machine.Pre-crack lengths of all specimens used in experiments are determined as indicated in the standard.Crack propagation during tests is monitored and controlled by using a high-zoom camera and divided sub-millimetric scales on specimens,and the number of cycles are recorded simultaneously(see Fig.1).Pre-crack and fatigue test loads are determined according to the ASTM condition ((Kmax)final-pre-cracking≤(Kmax)initial-testing).After generation of the pre-crack,fatigue crack growth tests are performed atR=0.1(whereRis the stress ratio)for all experiments.

3.1.Mode-I fatigue crack growth experiments

In this sub-section,fatigue crack growth experiments are performed by using CT specimens(see Fig.2)under pure mode-I loading to determine the fatigue crack growth rate data of the material used in the experiments.

The general fatigue crack growth behavior exhibited by most structural materials under constant-amplitude test conditions is described by the relationship between the crack growth rate,da/dN,and the stress intensity factor range,ΔK,in the lglg scale.In Fig.3,a typical fatigue crack growth curve including three regions is shown.Paris and Erdogan30discovered the following equation for Region II,in which stable crack growth exists and logarithm of the crack growth rate linearly increases with increasing lg ΔK:

whereCandnare crack growth-related material properties.ΔKis the SIF range and can simply be the mode-I SIF for mode-I loading conditions or an equivalent SIF,ΔKeqv,for mixed mode crack growth situations.ΔKfor a CT specimen under pure mode-I loading condition is calculated using the following formula according to the ASTM standard:

Fig.1 Experimental set-up.

Fig.2 Geometry and dimensions of a CT specimen.

Fig.3 Typical fatigue crack growth curve.

where ΔPis force range,ais crack length,BandWare the thickness and width of the specimen.

Fig.5 Comparisons of fatigue crack growth rates for Al 7075-T651,R=0.1.

In Fig.4,overall views of the CT specimens before and after tests are given.For each mode-I test,SIF ranges are calculated by using test load ranges and updated crack lengths based on crack growth increment measurements.Fatigue crack growth rate data of the material is plotted,and material constantsCandnare obtained as 1.46×10-6and 2.44,respectively(da/dNin ‘mm/cycle” andKin ‘MPa·m1/2”)byfitting the curves.Material constants obtained previously from the literature for Al 7075-T651 are substituted in Eq.(8),and the corresponding fatigue crack growth rate data are compared with the experimental data in the logarithmic scale(see Fig.5).It is seen from the figure that experimental data obtained in this study are close to those from the literature.31–34Thus,for all mixed mode simulations presented in this paper,material properties obtained from mode-I fatigue crack growth experiments are used to calculate crack propagation lives.

Fig.4 Overall views of CT specimens before and after tests.

3.2.In-plane mixed mode-I/II fatigue crack growth experiments

In-plane mixed mode-I/II fracture experiments are performed under different loading angles using pre-cracked CTS specimens(see Fig.6),which are widely used in the literature and proposed by Refs.21,35.

Mixed mode loading apparatus are designed to allow the loading axis to pass through the mid-point of the specimen width under different loading angles.Fatigue crack growth experiments are carried out for loading angles of 30°,45°,60°and 75°.10 mm thick specimens are used in the experiments.In Fig.7,overall views of the experimental set-up are shown.The crack growth rates during load cycle intervals are recorded concurrently for each mixed mode loading condition.Consistent fracture surfaces and de flection angles are observed from the tests for all loading angles.

4.Modeling of fatigue crack growth experiments

Fig.6 Dimensions of a CTS specimen.21,35

Experimental fracture surfaces of all broken specimens are scanned exactly and the mean crack surface is obtained by a surfacefit of the crack propagation planes for every mode mixity ratio,i.e.,loading angle.Fracture surface regions,i.e.,crack paths,are divided into equal spaces to model and analyze separately each incremental crack profile.Modeling and solution of the global problem,including all parts of the test system,for each mode mixity case are carried out using ANSYSTM36by defining contact mechanics between the specimen and the loading apparatus.In Fig.8,process steps involved in modeling of crack surfaces are shown representatively for the 9th crack propagation step under 30°loading angle.In an effort to simulate the real conditions as in the experiments,contacts are defined between the contact surfaces of the loading devices,pins and specimen.Boundary conditions are defined so that the surface nodes of the bottom loading clevis are constrained in all directions and those of the upper loading clevis are allowed to move along the loading axis only.Load is applied on the upper loading clevis in the vertical direction.Having obtained the overall global solution of the system using ANSYSTM,displacements are taken from nodes of the loading hole surfaces of the specimen by using submodeling.Then,these displacements are applied on the specimen model,and three-dimensional fracture analyses are performed using FRAC3D,a standalonefinite element program employing enrichedfinite elements to calculate the resulting SIFs as the main solver of FCPAS(Fracture and Crack Propagation Analysis System).37,38Having computed the mixed mode SIFs from the numerical analyses,equivalent SIFs on the crack fronts are calculated by substituting the SIFs(KIandKII)into the developed and existing mixed mode-I/II criteria,and life cycles are predicted for each criterion.Finally,crack propagation lives under different loading angles(30°,45°,60°and 75°)are compared with experimental results.

5.Numerical and experimental results

In this section,results obtained from numerical analyses of actual mixed mode-I/II fatigue crack growth experiments and comparisons of fatigue crack growth rates predicted using different criteria with experimental results are presented for different loading conditions.

Three pre-cracked CTS specimens are tested experimentally under 30°loading angle.In an effort to ensure that the corresponding ASTM fatigue crack growth test conditionis satisfied,specimens are tested under two different fatigue test loads.An 8.8 kN fatigue load(R=0.1)is applied to one specimen,labeled as CTS-01,and an 11 kN fatigue load(R=0.1)is applied to the other two specimens,labeled as CTS-02 and CTS-03.In Fig.9,front views of the broken specimens under the 30°loading angle are shown.Since fatigue pre-crack lengths measured after experiments are not always the same,in Fig.9,fracture surfaces are overlapped at the crack de flection point of the fatigue pre-crack surface,and the mean crack de flection angle is obtained by surfacefitting of the crack growth surfaces.Fracture analyses are performed by modeling the experimental crack surface for each crack propagation step until it reaches the starting point of unstable crack growth.In Table 1,SIFs obtained from center points of crack profiles and equivalent SIFs calculated using in-plane mixed mode-I/II criteria are given for the case of 8.8 kN fatigue loading.

Fig.7 Overall views of experimental set-up with a CTS specimen under 30°,45°,60°and 75°loading angles.

Fig.8 Process steps involved in modeling of crack surfaces for the 9th crack propagation step under 30°loading angle.

Crack propagation lives are evaluated by substituting the equivalent SIFs into Eq.(8)for each criteria.Numerical analysis results for the 8.8 kN fatigue load are also scaled to represent the 11 kN fatigue load and to compare the results in terms of crack growth lives.Variations in crack length as a function of number of load cycles under the 30°loading angle are presented for 8.8 kN and11 kN fatigue loads in Figs.10(a)and(b),respectively.As can be seen from the figures,all of the criteriaagree very well with the experimental results under different fatigue loads.

Table 1 Predicted equivalent SIFs according to mixed mode-I/II criteria for 30°loading condition(applied load is 8.8 kN).

Fig.10 Comparisons of fatigue crack growth lives predicted using different criteria and experimental data.

Table 2 Predicted equivalent SIFs according to mixed mode-I/II criteria for 45°loading condition(applied load is 11.4 kN).

Table 3 Predicted equivalent SIFs according to mixed mode-I/II criteria for 60°loading condition(applied load is 13.65 kN).

Table 2 summarizes the SIFs from the fracture analyses performed for incremental crack propagation steps under 45°loading angle for the crack front center point on the crack front and the corresponding equivalent SIFs according to different mixed mode-I/II criteria.11.4 kN fatigue loading is applied in the analyses.In Fig.10(c),comparisons between predicted crack growth lives by different criteria and experimental lives for the 45°loading condition are given.All of the criteria have about the same and close tendency as the experimental results for this loading condition.

In Table 3,SIFs obtained for the crack front center point from the fracture analyses performed for incremental crack propagation steps under 60°loading angle and corresponding equivalent SIFs according to mixed mode-I/II criteria are presented.13.65 kN fatigue loading is applied in the analyses.Crack lengths as a function of number of load cycles under the 60°loading angle are given in Fig.10(d).Similar to other loading conditions,all of the criteria provide similar and close predictions to the experimental data.

Finally,fracture analyses are performed for incremental crack propagation steps under 75°loading angle.As is with the 30°loading case,13 kN(R=0.1)and 15 kN(R=0.1)are applied separately in experiments and numerical analyses.In Fig.11,distributions of SIFs along the crack front for each crack propagation step for the case of 15 kN fatigue loading under the 75°loading angle are given and the related equivalent SIFs computed for the crack front center point according to mixed mode-I/II criteria are given in Table 4.It is seen from Fig.11 that,as expected,KIIandKIIIdecrease during crack growth whileKIincreases,i.e.,the mixed mode problem is converged to that of mode-I loading type,and eventually the crack continues to grow on a path perpendicular to the loading axis.The distribution ofKIIISIFs along the crack front is linear due to the Poisson’s ratio effect of the material.28It is also seen that the equivalent SIF obtained from the developed criterion28for the initial crack is much lower than that from the existing criteria.Although closer equivalent SIFs are obtained for lower mode mixity ratios using the developed and existing criteria,remarkable differences between them are observed for this loading angle.

As mentioned in the Section 1,most existing criteria show a deviation from experimental measurements under high mode mixity ratios according to some studies in the literature and a previous study.28Therefore,in the previous study,28a newly developed criterion involving highly mixed mode conditions was also proposed for in-plane mixed mode-I/II problems.Thus,significant differences are observed between existing criteria and the developed criterion for the initial crack in the 75°loading case.It is also seen that the equivalent SIFs for the later crack propagation steps are closer to each other.The reason is that,as the crack starts propagating under a mixed mode condition,the dominant mode type changes from mode-II to mode-I.SIF solutions obtained for the 15 kN fatigue load are scaled to represent the 13 kN fatigue load,and comparisons of crack growth lives predicted by criteria with experimental lives are given in Fig.12.The closest trend is obtained between the prediction made by the developed criterion and experimental crack growth lives under the 13 kN fatigue load(see Fig.12(a)).All of the criteria are in good agreement with the experimental results under the 15 kN fatigue load(see Fig.12(b)).An acceptable level of agreement is seen between experimental results and numerical crack growth rates calculated by the developed criterion for both loading cases under the 75°loading angle.

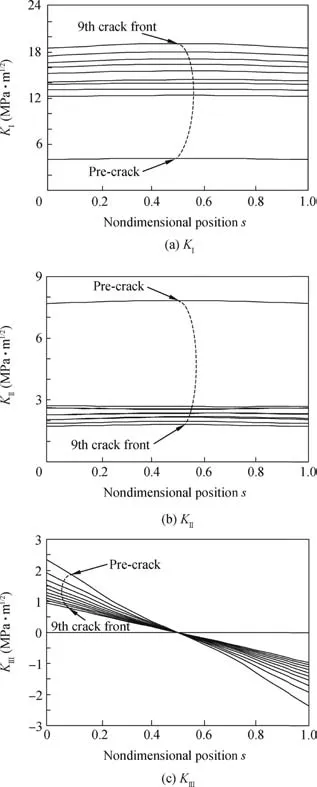
Fig.11 Distributions of mixed mode SIFs along the crack front for each crack propagation step under 75°loading angle.

6.Summary

In this study,in-plane mixed mode-I/II fatigue crack growth experiments are performed under different loading conditions(30°,45°,60°and 75°),and modeling and analyses of the experiments are carried out to evaluate the applicabilities of a criterion developed previously by the authors and different criteria available in the literature to mixed mode-I/II crack growth tests.Results show that all of the criteria are in goodagreement with the experimental lives for all loading conditions.Although significant differences are obtained from the developed criterion in terms of equivalent SIFs for the initial crack,similar equivalent SIFs are obtained for the later crack propagation steps under 75°loading angle.Since a high mode mixity condition changes to almost nearly a mode-I condition immediately after the first crack propagation step from the initial crack,a significantly notable decrease is observed inKII.Thus,closer crack growth lives are obtained between the used criteria and experimental data.Thus,crack growth lives are minimally affected by the difference obtained for the initial crack,yielding closer total crack growth lives between different criteria and experimental data.

Table 4 Predicted equivalent SIFs according to mixed mode-I/II criteria for 75°loading condition(applied load is 15 kN).

Fig.12 Comparisons of fatigue crack growth lives predicted using different criteria and experimental data under 75°degree loading angle.

Acknowledgements

This study was supported by the Scientific and Technological Research Council of Turkey(TUBITAK)(No.113M407).The ability of usage of an axial fatigue test machine at Bursa Technical University is gratefully acknowledged.