Numerical analysis of broadband noise reduction with wavy leading edge

Fn TONG,Weiyng QIAO,b,*,Weijie CHEN,Hoyi CHENG,Renke WEI,Xunnin WANG

aSchool of Power and Energy,Northwestern Polytechnical University,Xi’an 710129,China

bKey Laboratory of Aerodynamic Noise Control,China Aerodynamics Research and Development Center,Mianyang 621000,China

cState Key Laboratory of Aerodynamics,China Aerodynamics Research and Development Center,Mianyang 621000,China

KEYWORDS Aeroacoustics;Broadband noise;Large eddy simulation;Noise control;Noise reduction mechanism;Rod-airfoil interaction;Wavy leading edge

Abstract Large Eddy Simulation(LES)is performed to investigate the airfoil broadband noise reduction with wavy leading edge under anisotropic incoming turbulence.The anisotropic incoming turbulence is generated by a rod with a diameter of 10 mm.The incoming flow velocity is 40 m/s and the corresponding Reynolds numbers based on airfoil chord and rod diameter are about 397000 and 26000,respectively.The far- field acoustic field is predicted using an acoustic analogy method which has been validated by the experiment.A straight leading edge airfoil and a wavy leading edge airfoil are simulated.The results show that wavy leading edge increases the airfoil lift and drag whereas the lift and drag fluctuations are substantially reduced.In addition,wavy leading edge can significantly change the flow pattern around the leading edge and a pair of counter-rotating streamwise vortices stemming from each wavy leading edge peak are observed.An averaged noise reduction of 9.5 dB is observed with the wavy leading edge at the azimuthal angle of 90°.Moreover,the wavy leading edge can mitigate noise radiation at all the azimuthal angles without significantly changing the noise directivity.The underlying noise reduction mechanisms are then analyzed in detail.

1.Introduction

With the fast development of civil aviation industry,the associated environmental impact of aviation,including both air pollution and noise nuisance,is getting more and more attention.For example,stringent targets have been set in Europe for 2050,which aims at reducing noise emissions by 65%compared to the year of 2000.1The aerodynamic noise radiated from the interaction between the oncoming turbulence and the leading edge of an airfoil is one of the commonly encoun-tered types of noise problems and significantly contributes to the noise in many engineering applications,such as turbofan outlet guide vanes,contra-rotating open rotors and contrarotating fans.The airfoil-turbulence interaction noise,also known as Leading Edge(LE)noise,is often considered to be one of the major noise sources,especially in the presence of significant upstream disturbances.2

LE noise has been studied for many years and has been successfully modelled by Amiet3and Howe.4,5Amiet’s model explains the interaction noise by considering that the impinging turbulent eddies will undergo a sudden change in the boundary condition when they encounter the flat plate.The impinging turbulence should satisfy the condition of no flow through the airfoil and consequently induces a fluctuating pressure dipole source on the surface which then radiates to the far field.Amiet’s model was further extended by Roger and Moreau by accounting for the effects due to a limited chord length.6,7Howe’s4,5vortex sound theory explains the interaction noise in a similar fashion.According to Howe’s model,the velocity field generated by a vortex close to an airfoil induces dipole sources on the airfoil surface,which are proportional to the fluctuating normal forces.

The reduction of LE noise is a constant need for turbofan suppliers.Recently,the wavy leading edges inspired by the leading edge tubercles of humpback whales have been extensively investigated.Such a geometry was originally considered for its aerodynamic benefits of improving airfoil post-stall performance.The leading edge tubercles of humpback whales were firstly studied in detail by Fish and Battle8in 1995.It is suspected that the leading edge tubercles function as enhanced lift devices to control flow over theflipper and maintain lift at high angles of attack,thus increasing the maneuverability of the humpback whales.After Fish’s work,many studies showed that wavy leading edge can improve the airfoil post-stall aerodynamic performance,whereas the pre-stall aerodynamic performance is reduced a little.9–12The adverse effect,however,can be reduced by optimizing the profile of the wavy leading edge.13

The effects of wavy leading edges on the aeroacoustic noise have also been extensively investigated in the recent years.14–28According to the authors’knowledge,Hansen et al.14carried out the first experiment to investigate the acoustic effects of wavy leading edges on the NACA0012 airfoil noise.It was found that the wavy leading edge can significantly reduce airfoil tonal noise(approximately 4–8 dB).They supposed that the formation of streamwise vortices around the wavy leading edge profile was responsible for the reduction in tonal selfnoise since the streamwise vortices can break up the coherence of vortex generation at the trailing edge.In addition,a reduction of broadband LE noise has also been observed for airfoils/plateswith wavy leading edges.15–21Clairetal.15experimentally and numerically investigated the effects of wavy leading edges on the airfoil-turbulence interaction noise and a broadband noise reduction of 3–4 dB was reported.

An experimental parametric study was carried out by Narayanan16and Chaitanya17,18et al.Narayanan et al.16found that leading edge serrations are more sensitive to the serration amplitude than the serration wavelength and the noise reduction effects increase as the serration amplitude increases,which is also supported by the experimental results of Chaitanya et al..18An optimum serration wavelength is identified by Chaitanya et al.18,which is roughly four times the integral length scale.A simple scaling law was also derived by Chaitanya et al.,which can predict the noise reduction for arbitrary serration amplitude and wavelength.Chaitanya also pointed out that the noise reduction mechanism is complicated and the variations in the phase of the serrated leading edge is not the only noise reduction mechanism.18The acoustic benefits ofinnovative leading edge geometries,such as dualfrequency,chopped-peak and slitted-root serrated airfoils,have also been experimentally investigated to achieve further noise reduction.19,20Chong et al.21also carried out similar experimental study and both aeroacoustic and aerodynamic performance of a serrated airfoil was investigated.

A lot of effort was also taken to develop analytical models to predict the noise reduction effects of wavy leading edges.22–24Roger et al.22extended Amiet’s model and developed an analytical model for the sound generation due to interaction between incoming turbulence and a serrated plate,where the wavy leading edge is considered as a periodically varying sweep.It is found that the supercritical or subcritical character of the local impingement of a gust is a key parameter for the noise reduction.The model also suggests that the Mach number plays a significant role in the effectiveness of serrations.Mathews and Peake23analyzed the noise radiated from serrated flat plate using the Green’s function and found that it is difficult to predict the optimum level of serrations.Actually,we cannot hope that one serration will reduce the noise for all parameters of eddies,which is also supported by Chaitanya et al.17,18A generalized Amiet’s model was also derived using the Fourier expansion and the Schwarzschild techniques to predict the LE noise with serrated leading edges by Lyu et al.,24and the theoretical result agrees well with experimental result which suggests that the model captures the essential physics of the serrated/wavy leading edges.

At the meantime,several numerical studies have also been carried out to deal with the noise reduction by wavy leading edges.25–28Lau et al.25numerically investigated the effects of wavy leading edges on the Airfoil-Gust Interaction(AGI)noise.A harmonic gust of the incoming flow is considered.Extensive parametric study was conducted and it was found that the ratio of the wavy leading edge peak-to-peak amplitude to the longitudinal wavelength of the incident gust was an important factor to reduce AGI noise.Kim26and Turner27et al.also carried out extensive numerical investigation of the LE noise reduction by using the wavy leading edges where the interaction between the incoming turbulence generated by a synthetic eddy method and a serrated leading edge flat plat is considered.More recently,Aguilera et al.28carried out numerical investigation of the wavy leading edge interacting with anisotropic turbulence.It is found that the noise reduction caused by wavy leading edge is sensitive to the length scales of vortical disturbances.

Despite the rapid growth in this field,the understanding of the noise reduction mechanisms associated with wavy leading edge is still underdeveloped.27Moreover,most of the investigation of noise reduction using wavy leading edges is experimental study under homogeneous isotropic turbulence.16–18,21Though valuable guidelines are obtained in terms of noise reduction laws,experimental results only provide afinite amount of flow field information which may hinder the further understanding of noise reduction mechanisms.The detailed measurement of the unsteady flow field around the tiny struc-tures of wavy leading edge is still a challenging work.Therefore,an accurate numerical study of the flow field over a wavy leading edge airfoil helps to further analyze and better understand the flow characteristics around the wavy leading edge as well as the underlying noise reduction mechanisms.In addition,the turbulence encountered in many engineering applications is actually anisotropic,for example,the rotor wake in turbofans.Therefore,there is also a need to estimate the noise reduction effects of wavy leading edge under more realistic turbulence.

Considering the above factors,this paper aims at(A)estimating the broadband noise reduction effects under anisotropic incoming turbulence, (B) revealing the flow characteristics around the wavy leading edge and the underlying noise reduction mechanisms.

This paper is organized as follows.Firstly,the numerical methods for flow field and acoustic field are described in Section 2.Then the numerical model and numerical setup are presented in Section 3.The results and analysis are discussed in Section 4.Finally,the conclusions are given in Section 5.

2.Methodology

2.1.Numerical method for flow field

As broadband noise is concerned in the current paper,the broadband nature of the noise sources should be captured by the simulation,which generally requires Direct Numerical Simulation(DNS)or Large Eddy Simulation(LES).LES is used to compute the flow field in this paper.

In LES,the large and small scales of the flow are treated differently according to their different characteristics.Generally speaking,large scales of the flow contain the main part of the total fluctuating kinetic energy and characterize the flow.They drive the physical mechanisms of the flow.At the same time,the large scales of the flow are sensitive to the boundary conditions and are anisotropic.29In contrast,small scales of the flow contain only a few percent of the total kinetic energy and have weak influence on the meanfluid motions.Their main function is viscous dissipation.In LES,the large three-dimensional unsteady turbulent motions are directly solved,whereas the effects of the smaller-scale motions are modelled by the SubGrid-Scale(SGS)stress model.

In the current paper,the commercial available solver CFX30is used to calculate the flow field and the dynamic Smagorinsky-Lilly model31is used whose model coefficient can adjust automatically to the flow type according to the information contained in the resolved turbulent velocity field.This model has demonstrated satisfactory results by Winkler32and the authors’previous study.33

2.2.Far- field noise prediction

The far- field noise prediction method is based on Goldstein’s generalized Lighthill equation.34The fundamental equation governing the generation of sound in the presence of solid boundaries is presented below34:

wherec0is the ambient speed of sound,ρ0is the ambient density and ρ′is the acoustic density disturbance.x= ［x1x2x3］ is the observer location and y= ［y1y2y3］is the sound source location.At sufficient distance from the sourceis equal to the acoustic pressurep′.τ is the time at the sound source(retarded time),tis the time at the observer location,Tis the time integral limit,andSis the integral area.is the velocity of the surface normal to itself relative to thefluid.Gis the Green’s function,fiis the force of a solid boundary acting on thefluid in theith direction.ν is the volume integral region,andis the Lighthill stress tensor.

When the incoming flow Mach number is small and the solid surface keeps statistic,which is often the case in the acoustic wind tunnel experiments,the first and third term on the right hand of Eq.(1)can be ignored.Therefore,Eq.(1)can be simplified as

Gis the free space,moving medium,time dependent Green’s function expressed as follows:

where δ is the Dirac delta function,Ris the amplitude radius

and σ is the phase radius with β2=1-M2

whereU0is the uniform velocity of the moving medium andMis the Mach number.More details about the noise prediction method can be found in Ref.33.For clarity,only the final expression for the far- field acoustic pressure is presented herein as follows33:

where ω is the angular frequency andGωis the form of Green’s function in the frequency domain.33

3.Model and numerical setup

3.1.Model

Fig.1 Model and computational domain.

A NACA65-(12)10 airfoil placed downstream of a rod is considered in this study,as shown in Fig.1.The airfoil chord isc=150 mm and the rod diameter isd=10 mm.The distance between the rod and the airfoil leading edge is 100 mm,i.e.0.66c.The canonical rod-airfoil configuration is chosen in this paper because this configuration combines the periodic vortex shedding with a random perturbation due to the wake’s transition into turbulence.The airfoil undergoes a broadband perturbation which isdominated byapreferred shedding frequency,somewhat like that observed in turbomachinery applications.35In addition,unlike the harmonic gust and synthetic turbulence,rod wake can produce more realistic turbulence and the rod wake turbulence is anisotropic.

In order to investigate the effect of wavy leading edges on the turbulence-airfoil interaction noise,an airfoil with modified leading edges,i.e.wavy leading edges,is designed,as shown in Fig.2.The wavy leading edge is defined by peakto-root amplitudeAand wavelength λ whereA=0.3cand λ=0.2c.These parameters are chosen according to the experimental results of Chaitanya17,18and Chong21et al.who suggest that a slender wavy leading edge is more preferred to obtain large noise reduction.Airfoil profiles at different span locations,i.e.peak,hill and trough,are also shown in Fig.2(b).The straight leading edge case will be denoted as straight LE while its counterpart wavy leading edge case will be denoted as wavy LE hereafter.

3.2.Numerical setup and boundary conditions

The sketch of computational mesh around the rod and airfoil is shown in Fig.3.An O-type topology is used to generate the mesh around the rod and airfoil.The computational domain extends 33cin the streamwise direction(xdirection),and 26cin the vertical direction(ydirection),as shown in Fig.1.In the spanwise direction,the domain extends 0.4c(or 6d)which is sufficient to capture the spanwise flow features.35

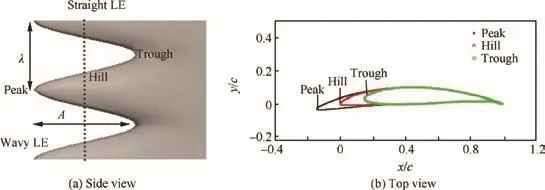
Fig.2 Sketch of wavy leading edge.

Fig.3 Sketch of computational mesh.

In order to make sure that the computational result is independent of the grid,a mesh sensitivity study is carried out with three different mesh sizes comprising 4.3,7.9 and 12.3 million grid nodes,respectively.The three different meshes have 30,55 and 85 nodes along the spanwise direction(zdirection),while the mesh nodes distribution along thex-yplane remains the same.Fig.4 shows the dimensionless grid size distribution along the streamwise direction and wall normal direction.It can be seen that wall normal mesh dimensionless size Δy+is less than 1 and streamwise mesh dimensionless size Δx+is less than 100 over most of the airfoil surface,which is in accordance with the suggestion of Wagner et al.29Moreover,the authors’previous simulation for a similar configuration33indicates that the grid size inx-yplane is sufficient.

The mesh sensitivity study results are shown in Fig.5.Fig.5(a)shows the Power Spectrum Density(PSD)of the airfoil lift coefficientCLand drag coefficientCD.Fig.5(b)shows the Sound Pressure Level(SPL)results computed from three different meshes.It can be seen that all the three meshes capture the periodic vortex shedding frequency at a Strouhal number ofSt=fd/U0=0.195(wherefis frequency)and the spectral broadening around the vortex shedding frequency due to the turbulence is well captured.It can be seen from Fig.5 that the three different meshes give consistent results.The sound pressure levels at the vortex shedding frequency are 69.0,65.8 and 64.5 dB for grid nodes of 4.3,7.9 and 12.3 million respectively.The difference of sound pressure level predicted by the grid nodes of 7.9 and 12.3 million is very small.The mesh sensitivity study shows that both meshes can give reasonable prediction results.Finally,the medium mesh(7.9 million)is chosen for the straight LE case.For the wavy LE case,the grid nodes in the spanwise direction is increased to 85 considering the spanwise geometry complexity for the wavy LE case which results in grid nodes of 11.5 million.

The boundary conditions are set as follows.The velocity inlet is used for the inlet with the velocity ofU0=40 m/s and the pressure outlet is set for the outlet.Periodic conditions are used in the spanwise direction and opening condition is used in the vertical direction,as shown in Fig.1.Adiabatic no-slip conditions are used on the rod and the airfoil.

Fig.4 Dimensionless grid size distribution.

Fig.5 Mesh sensitivity study.

In this paper,the dynamic Smagorinsky-Lilly model and thesecond-orderbackward Eulertransientschemeare adopted,similar to the simulation in Ref33.The time step is 1×10-5s and the total acquired physical time for acoustic processing is about 0.12 s which corresponds to a time interval during which the incoming flow passes the airfoil chord about 32 times.

4.Results and analysis

4.1.Aerodynamic and acoustic performance

The characteristics of the incoming turbulence atx/c=-0.2 are firstly examined in Fig.6.The difference between the Root Mean Square(RMS)values of velocity fluctuations in three different directions(u,v,w)is clearly observed in Fig.6(a).The PSD of velocity fluctuations in three different directions is also shown in Fig.6(b).It can be seen that there is a broadened peak in the PSD of the streamwise and vertical velocity fluctuations,whereas the broadened peak is absent in the PSD of the spanwise velocity fluctuation.The incoming turbulence in the current paper is different from the grid-generated turbulence which is generally considered as homogeneous and isotropic.

The aerodynamic and acoustic performance of the wavy LE case is compared with the straight LE case.The comparison of time averaged pressure coefficient distribution on the airfoil is shown in Fig.7 where the time averaged pressure coefficientCpis defined as

where 〈p〉is the time averaged statistic pressure andp0is the ambient absolute pressure.

It can be seen from Fig.7 that wavy LE has an influence on the pressure coefficient distribution but this influence is limited to the region upstream ofx/c=0.4.Downstream ofx/c=0.4,the effect of the wavy leading edge on the pressure coef ficient is negligible.For the wavy LE case,the pressure coef ficient distribution upstream ofx/c=0.4 is different at three different span locations,i.e.peak,hill and trough locations.An important feature is that the pressure coefficient on the airfoil suction side undergoes more and more sudden change from peak location to trough location.Moreover,a local minimum of the pressure coefficient is observed on the suction side near the leading edge at the trough location,which is marked as region ‘A” in Fig.7.It will be shown later that this local minimum of pressure has an impact on the flow characteristics near the leading edge.

Fig.6 Characteristics of incoming turbulence at x/c=-0.2.

Fig.7 Time averaged pressure coefficient distribution.

The time histories of airfoil lift and drag coefficients are shown in Fig.8.The lift coefficientCLand drag coefficientCDare defined as

whereFxandFyare the forces on the airfoil inxandydirections,respectively,andLis the airfoil span.It can be seen from Fig.8 that wavy LE can significantly reduce lift and drag coeffi cient fluctuations while the mean lift and drag coefficients do not vary too much.In order to quantify the difference more clearly,the mean and RMS values of the lift and drag coef ficients are presented in Fig.9(a)and(b)respectively.It can be seen in Fig.9(a)that the mean lift coefficient is increased from 0.5029 to 0.5280(by about 5.0%)while the RMS value of lift coefficient is reduced from 0.1097 to 0.0380(by about 65.4%).The mean drag coefficient is increased from 0.0009 to 0.0039(by about 333.3%)and the RMS value of the drag coefficient is reduced from 0.0105 to 0.0030(by about 71.4%).

Fig.8 Time histories of airfoil lift and drag coefficients.

Fig.10 shows the comparison of PSD of the lift and drag coefficient fluctuations between the straight LE case and wavy LE case.It can be seen that both the lift and drag coefficient fluctuations are significantly reduced in a wide frequency range(0.1＜St＜1.4).Moreover,the reduction seems to be more obvious at mid to high frequency range(St＞0.3).For example,the lift and drag coefficient fluctuations are reduced by 11.5 dB and 13.8 dB respectively atSt=0.3,14.7 dB and 16.7 dB respectively atSt=0.6,and 13.3 dB and 20.8 dB respectively atSt=1.4.

Fig.11 shows the comparison of the acoustic performance between the straight LE case and wavy LE case.Fig.11(a)shows the results of sound pressure level at a distance of 2.0 m and azimuthal angle of 90°relative to the airfoil center.The azimuthal angle of 0°denotes downstream direction(positivexdirection),180°denotes upstream direction(negativexdirection),and 90°denotes the upside direction relative to the airfoil suction side surface(positiveydirection).Fig.11(b)shows the results of OverAll Sound Pressure Level(OASPL)computed fromSt=0.1 toSt=1.4.It can be seen from Fig.11(a)that wavy LE can significantly reduce the sound pressure level,especially in frequency range ofSt＞0.25.In addition,a significant reduction of OASPL at various azi-muthal angles is observed.The noise reduction by wavy LE is slightly more obvious at upstream direction(180°)than that at downstream direction(0°).For example,the noise reduction of OASPL is 9.0 dB at 0°and 11.2 dB at 180°.In order to quantify the noise reduction more clearly,Fig.12 shows the noise reduction ΔSPL defined as follows:

Fig.9 Comparison of mean and RMS values of airfoil lift and drag coefficients between straight LE case and wavy LE case.

Fig.10 Comparison of PSD of airfoil lift and drag coefficient fluctuations between straight LE case and wavy LE case.

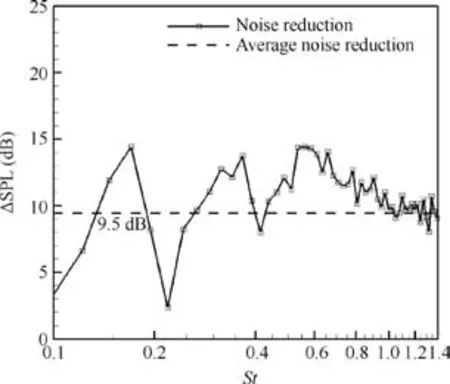
Fig.12 Sound pressure level reduction(at a distance of 2.0 m,azimuthal angle of 90°).

Fig.11 Comparison of acoustic performance between straight LE case and wavy LE case.

It can be seen in Fig.12 that the noise reduction is more pronounced in mid to high frequency range and the maximum noise reduction can be about 14.5 dB.The mean noise reduction level is also marked with a dashed line,which represents a value of 9.5 dB.

4.2.Flow field characteristics

The time averaged pressure distribution on the airfoil suction side surface is displayed in Fig.13.It can be seen from Fig.13 that the pressure distribution along the spanwise direction is substantially changed due to the wavy leading edge modification.A periodicity of the pressure distribution along the span is observed for the wavy LE case with a low pressure region located just downstream of the wavy leading edge trough,which is in line with Fig.7.

Fig.14 shows the time averaged wall shear τwdistribution along the airfoil pressure side and suction side for the straight LE case and wavy LE case.For the straight LE case,τwis most prominent along the airfoil leading edge,both for the pressure side and suction side.τwon the suction side is higher than that on the pressure side.Compared with the straight LE case,wavy LE case shows a significant reduction in τwalong the airfoil leading edge,especially around the wavy leading edge hill location.However,τwaround the wavy leading edge trough is increased a little.Further downstream of the trough,a region of low τwis observed,as shown in Fig.14(b)and(d).

The time averaged spanwise component of wall shear(wall shear inzdirection)distribution on airfoil suction side surface is shown in Fig.15.It can be seen thatfor the straight LE case is much smaller than that for the wavy LE case.For the wavy LE case,a local positive and negative extremum region ofis located oppositely around the wavy leading edge peak and trough location,which indicates strong spanwise flow in opposite direction around here.To confirm this conjecture,Fig.16 presents the spanwise mean velocity(VelocityUavg_z)distribution on various slices along the airfoil chordwise direction.It can be seen from Fig.16 that the presence of wavy leading edge leads to significant flow nonuniformity along the spanwise direction.As the incoming flow impinges onto the wavy leading edge peak,the wavy leading edge peak tends to divert the flow into two different directions,i.e.positivezdirection and negativezdirection,which is in accordance with the spanwise component of wall shear distribution shown in Fig.15(b).

The strong flow non-uniformity along the spanwise direction can also induce streamwise vorticity.The time averaged streamwise vorticity at various slices along the airfoil chordwise direction(VorticityVavg_x)is compared between the straight LE case and wavy LE case in Fig.17.It can be seen that for the straight LE case,the distribution of streamwise mean vorticity is more like chaotic and the magnitude of the streamwise vorticity is small.However,for the wavy LE case,a periodic distribution of time averaged streamwise vorticity along the spanwise direction is observed,as shown in Fig.17(b)and(d).In addition,the streamwise vorticity on the pressure side is more prominent than that on the suction side due to a slight negative attack angle near the wavy leading peak location.In order to present the streamwise vortices more clearly,the instantaneous streamlines colored by streamwise vorticity are also displayed in Fig.17(c)and(d).It can be seen that a pair of counter-rotating streamwise vortices stemming from around the wavy leading edge peak are noticeable for the airfoil with wavy leading edge,whereas this phenomenon is not observed for the airfoil with straight leading edge.As the streamwise vortices move downstream,they tend to move towards the trough location and lead to a local low pressure region there,as shown in Fig.13.This phenomenon is also observed experimentally and numerically by Custodio10and Turner27et al.

Fig.13 Time averaged pressure distribution on airfoil suction side surface.

Fig.14 Time averaged wall shear τwdistribution.

Fig.15 Time averaged spanwise component of wall sheardistribution along airfoil suction side surface.

Fig.16 Spanwise mean velocity distribution.

Fig.17 Time averaged streamwise vorticity.

Fig.18 Time averaged streamwise vorticity and local flow vectors(x/c=0).

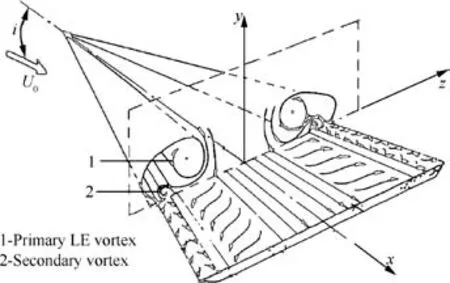
Fig.19 Schematic of flow over a delta wing.36

To further investigate the flow pattern around the wavy leading edge,Fig.18 shows the time averaged streamwise vorticity and the local flow vectors atx/c=0.It can be seen that a pair of streamwise counter-rotating vortices can be clearly identified at the airfoil pressure side,which is marked as vortex‘A” and vortex ‘B”.Vortex ‘A” rotates counterclockwise and vortex ‘B”rotates clockwise,which is referred to as the primary streamwise vortex structure.In addition to the primary streamwise vortex structure,secondary substructures are also identified,which are marked as vortex ‘C” and vortex ‘D”.The primary streamwise vortex structures and substructures observed here are similar to the vortex structures found in a delta wing,36,37as shown in Fig.19.

4.3.Noise reduction mechanism

To investigate the noise reduction mechanism,Fig.20 shows the comparison of wall pressure fluctuation amplitudepampon airfoil suction side surface at two different Strouhal numbers,i.e.St=0.195 andSt=0.488.It is noted that the legend range is different for Fig.20(a)and(b).It can be seen from Fig.20 that the wall pressure fluctuation is most prominent around the airfoil leading edge due to the strong interaction here between the incoming turbulence and the airfoil leading edge.Compared with the straight LE case,the wavy LE case shows a significant reduction of the wall pressure fluctuation intensity.Moreover,the reduction of the wall pressure fluctuation amplitude is more obvious at locations around the wavy leading edge hill.The wall pressure fluctuation amplitude around the wavy leading edge peak and trough is greater than that around the wavy leading edge hill.

Fig.21 Monitor points along airfoil leading edge.

Fig.20 Comparison of wall pressure fluctuation amplitude on airfoil suction side surface.

Fig.22 Comparison of power spectral density of wall pressure fluctuation along airfoil leading edge.

To further analyze the wall pressure fluctuation around the airfoil leading edge,33 monitor points are equally distributed along the airfoil leading edge,as shown in Fig.21,where the wavy leading edge peak(N0 point),hill(N4 point)and trough(N8 point)are clearly defined.Fig.22 compares the PSD of pressure fluctuation along airfoil leading edge between the straight LE case and wavy LE case.It should be pointed out that the PSD of wall pressure fluctuation is almost uniform along the span for the straight LE case.Therefore,only the spectrum at N0 point is shown for the straight LE case.It can be seen that the wavy leading edge can significantly reduce the PSD of the wall pressure fluctuation,especially at locations around the wavy leading edge hill.A consistent decrease of PSD of wall pressure fluctuation is observed from N0 to N6 point for the wavy leading edge case and this phenomenon is more obvious in low to medium frequency range whenSt＜0.6.However,the PSD of wall pressure fluctuation rebounds from N6 to N8 point.Finally,both of the wavy leading peak and trough yield high amplitude of PSD of wall pressure fluctuation,as shown in Fig.22.Overall,wavy leading edge is beneficial to reduce the PSD of the wall pressure fluctuation on the airfoil surface,which can result in reduced unsteady lift/drag fluctuation on the whole as shown in Fig.10.According to Eq.(7),the reduced wall pressure fluctuation intensity(hence lower unsteady force)is beneficial for the noise reduction.This mechanism can also be interpreted in a simpler way.For farfield sound pressure radiated from low Mach number flow,the contribution of quadrupole sources can be neglected.38Thus the far- field sound pressure due to dipole sources can be calculated as

whereniis the surface outward unit normal inith direction,pis the statistic pressure on the airfoil surface andris the distance between the observer and the sound source.If the size of the body is much smaller than the wavelength of sound,Eq.(12)can be converted to the time derivative form using an assumption of plane propagating sound waves39:

It can be seen from Eq.(13)that the far- field sound pressure is proportional to the time derivative of force fluctuation.Therefore,the reduced wall pressure fluctuation and force fluctuation(shown in Figs.9 and 10)due to the wavy leading edge can lead to a corresponding reduction of noise.

Apart from the above discussed mechanism,i.e.reduced wall pressure/force fluctuation,other mechanisms may also affect the noise reduction.The Cross Power Spectral Density(CPSD)between N0 point and other points is shown in Fig.23.The CPSD is defined as follows:

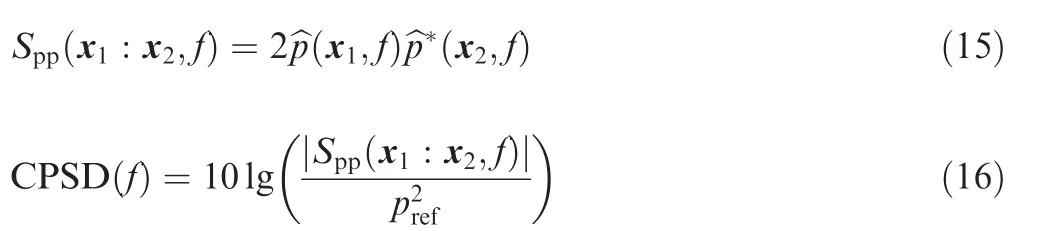
where（x1，f）is the Fourier transform of the surface pressure fluctuation at x1and（x2，f）is the conjugation of the Fourier transform of the surface pressure fluctuation at x2.Spp（x1:x2，f）is the cross-spectrum of the pressure fluctuation signalat x1and x2,and the reference pressure ispref=2×10-5Pa.

Fig.23(a)shows the CPSD between N0 and N1 and Fig.23(b)shows the CPSD between N0 and N4.It can be seen that when the leading edge is modified,the CPSD between different points along the leading edge is significantly reduced.It should be noted that the wall pressure PSD level for the wavy LE case is substantially smaller than that for the straight LE case.Hence,there is a possibility that the results presented in Fig.23 might have been biased towards producing a smaller level of CPSD for the wavy LE case.This issue is also discussed by Chong and Vathylakis40during their investigation of serrated trailing edges.To investigate this question further,the wall pressure raw data is normalized with the root mean square pressure(prms)and then the ‘normalized” PSD and CPSD can be calculated,similar to the treatment by Chong and Vathylakis40.It can be seen from Fig.24 that the normalized spectra collapse well for the straight LE case and wavy LE case.The normalized CPSD between different points is presented in Fig.25.A reduction of CPSD can still be observed for the wavy LE case compared with straight LE case,which further confirms the reduction of correlation level with wavy leading edges.

To further investigate the correlation between different points,correlation coefficientRppis defined as

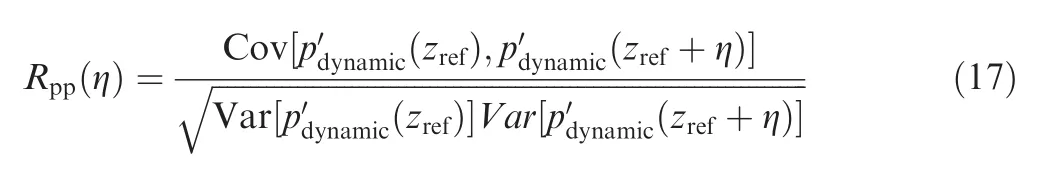
where Cov(a,b)represents the covariance between vector a and b and Var(a)indicates the variance of vector a.and（zref+ η）are the dynamic pressure fluctuations at the spanwise location ofzrefand a different spanwise location with η apart.Fig.26 shows the comparison of correlation coeffi cient between straight LE case and wavy LE case along the leading edge where the point in the middle span(N0)is chosen as the reference point.It can be seen from Fig.26 that for the straight LE case,the correlation coefficient monotonously decreases as the spanwise separation η increases.However,for the wavy LE case,the correlation coefficient fluctuates as the spanwise separation η increases.More specifically,the correlation coefficient decreases from N0 point to N6 point and then rebounds from N6 point to N8 point,which is in accordance with Fig.22.This suggests that the wall pressure fluctuation at N0 point(wavy LE peak)and N8 point(wavy LE trough)is similar to some extent.

Fig.23 Cross power spectral density between different points.

Fig.24 Normalized wall pressure power spectral density.

In addition,spatial coherence along the airfoil leading edge is also investigated.The spatial coherence γ2is defined as follows:

Fig.27 shows the spatial coherence contour for straight LE case and wavy LE case.It is noted that the N0 point is chosen as the reference point in Fig.27.It can be seen from Fig.27 that the spatial coherence at the vortex shedding frequency(St=0.195)is much higher than that at other frequencies,which is similar to the finding of Kato et al.39for a rod in low Mach number flow.

To quantify the difference of spatial coherence more clearly,Fig.28 shows the comparison of spatial coherence between the straight LE case and wavy LE case at two different Strouhal numbers,St=0.195 andSt=0.488.Now the high level of spatial coherence at vortex shedding frequency can be observed more clearly.For the straight LE case,the spatial coherence monotonously decreases as the spanwise separation increases atSt=0.195.However,for the wavy LE case,the spatial coherence first decreases then increases and then decreases again as the spanwise separation increases,which is similar to the phenomenon observed in Fig.26.The relative high level of spatial coherence observed when the spanwise separation η is 0.1cfor the wavy LE case atSt=0.195 is due to a kind of similarity between the wall pressure fluctuation at N0 point and N8 point,which is in line with Fig.26.AtSt=0.488,the spatial coherence decreases much faster as the spanwise separation increases.Overall,the wavy leading edge reduces the spatial coherence significantly,which indicates a reduced spanwise coherence lengthLc（ω）.

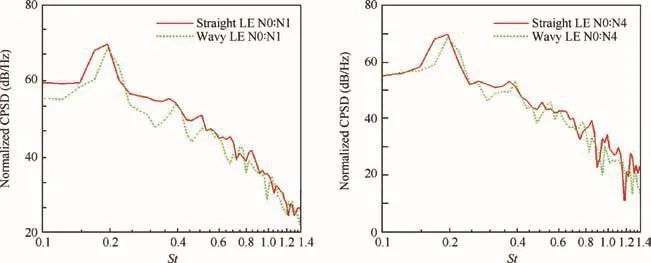
Fig.25 Normalized cross power spectral density between different points.

Fig.26 Comparison of correlation coefficient between straight LE case and wavy LE case.

Fig.27 Comparison of spatial coherence contour between straight LE case and wavy LE case.

The square root of the spatial coherence can be assumed to follow a Gaussian distribution with separation distance η as follows41:

Fig.28 Comparison of spatial coherence between straight LE case and wavy LE case at different Strouhal numbers.

Thus the spanwise coherence lengthLc（ω）at different Strouhal numbers can be obtained byfitting the square root of the spatial coherence data using the method of least squares.Fig.29 shows the comparison of square root coherence data between the straight LE case and wavy LE case at three different Strouhal numbers,St=0.195,0.391,0.488.Thefitting curves using Eq.(19)are also presented for the straight LE case using dashed lines.The derived spanwise coherence length from Eq.(19)is 0.272catSt=0.195,0.063catSt=0.391,and 0.039catSt=0.488 for the straight LE case.It should be noted that the square root of the spatial coherence data of the wavy LE case cannot be described very well by Eq.(19).Therefore,thefitting curves for wavy LE case are not shown here.Even though,Eq.(19)is useful to qualitatively analyze the results.According to Eq.(19),as the spanwise coherence length decreases,the square root of the spatial coherence will decay faster with the separation distance.Therefore,the faster decay of γ with the increase of separation distance for the wavy LE case indicates a reduced spanwise coherence length compared with the straight LE case.According to Amiet’s3theory,the far- field acoustic power spectral density produced by an airfoil in a subsonic turbulent stream is proportional to the spanwise coherence length scale.Therefore,it can be reasonably supposed that the reduction of the spanwise correlation level and the coherence length is another noise reduction mechanism of the wavy leading edge.

Fig.29 Comparison of square root coherence between straight LE case and wavy LE case at different Strouhal numbers.

Fig.30 Wall pressure fluctuation phase(cos φ)distribution on airfoil suction side surface.

Chaitanya et al.18developed a very simple,idealized model to predict the noise reduction with wavy leading edge by assuming that noise reduction is due to variations in the phase of wavy leading edge.A simple function was derived whose minima match very well the experimental data,which indicates that the variations in the phase caused by the wavy leading edge is one of the noise reduction mechanism.To examine the phase variation,Fig.30 shows the wall pressure fluctuation phaseppha(cos φ)distribution on airfoil suction side surface at two different Strouhal numbers,i.e.St=0.195 andSt=0.488.The wall pressure fluctuation phase φ is defined as

It can be seen from Fig.30(a)that the phase distribution is relatively uniform along the span for the straight LE case,whereas the phase distribution shows a less uniform characteristic especially around the leading edge for the wavy LE case.At higher frequency ofSt=0.488,the phase distribution tends to be more complex.The positive phase regions and negative phase regions are alternately distributed along the streamwise and spanwise direction and this alternate distribution is more prominent for the wavy LE case.Interestingly,a profile similar to the wavy leading edge geometry profile can be observed for the wavy LE case,which is marked as a dashed line in Fig.30(b).The alternate distribution of positive phase regions and negative phase regions is beneficial to reduce the correlation of the sound sources and can lead to a destructive interference of the sound sources.

To demonstrate the phase variation more clearly,Fig.31 shows the comparison of wall pressure fluctuation phase distribution along the airfoil leading edge atSt=0.195 andSt=0.488.The corresponding locations of N0 to N8 shown in Fig.21 are also marked with dotted lines for better interpretation of the phase variation.It can be seen from Fig.31(a)that while the phase distribution remains almost uniform along the leading edge for the straight LE case atSt=0.195,the phase distribution shows quasi-periodic behavior for the wavy LE case.More specifically,the phase distribution undergoes a cycle from N0 point and N8 point(i.e.from wavy leading edge peak to trough).Moreover,the pressure fluctuation at N0 point(wavy leading edge peak)and N4 point(wavy leading edge hill)are almost out of phase at the vortex shedding frequency.Fig.31(b)shows the wall pressure fluctuation phase distribution atSt=0.488.It can be seen that as the frequency increases,the phase distribution becomes increasingly complex.And the phase variation for the wavy LE case is always much greater than that for the straight LE case,which indicates a much more pronounced destructive phase interference for the wavy LE case.The destructive phase interference would yield lower noise level in the acoustic far field and hence is supposed to be another noise reduction mechanism.

5.Conclusions

(1)Wavy leading edge can substantially reduce airfoil unsteady forces.Airfoil lift and drag fluctuations are reduced by 65.4%and 71.4%respectively.In addition,wavy leading edge can significantly change the flow pattern around the leading edge and a pair of counterrotating streamwise vortices stemming from wavy leading edge peak are identified.

(2)The wavy leading edge can also substantially reduce turbulence airfoil interaction noise when the incoming turbulence is anisotropic and an averaged noise reduction of 9.5 dB is observed.The use of wavy leading edge can mitigate noise radiation at all the azimuthal angles without significantly changing the noise directivity.

(3)The noise reduction mechanism associated with wavy leading edge is also investigated.It is found that the following three mechanisms contribute to the noise reduction:(A)The wavy leading edge can substantially reduce the airfoil wall pressure fluctuation intensity along the airfoil leading edge,especially at regions around the wavy leading edge hill location.In the macro point of view,the overall lift and drag fluctuations can also be greatly suppressed,leading to a reduced sound source strength.(B)The correlation level and spanwise coherence length of wall pressure fluctuations are successfully reduced by the wavy leading edge.According to Amiet’s theory,the reduction of airfoil spanwise coherence length helps to reduce the turbulence-airfoil interaction noise.(C)The wavy leading edge produces a much more intense phase variation along the airfoil leading edge,which leads to a destructive phase interference.

Acknowledgements

This work was supported by the National Natural Science Foundation of China(Nos.51776174,51476134,51276149 and 11602290),State Key Laboratory of Aerodynamics of China Aerodynamics Research and Development Center(No.SKLA20160201)and Key Laboratory of Aerodynamic Noise Control of China Aerodynamics Research and Development Center(No.ANCL20170201).Special acknowledgement is given to China-Europe IMAGE(Innovative Methodologies and Technologies for Reducing Aircraft Noise Generation and Emission)program(No.688971-IMAGE-H2020MG-2014-1015).