一种便于实时传输的中值滤波算法

（青岛大学 自动化与电气工程学院，青岛 266071）

0 引言

在当今社会，实时视频传输在我们日常生活、工程、军事、医疗等各个方面都有着极其广泛的应用。我们看到的图像在其生成、传输、和处理的过程中，会不可避免地存在椒盐噪声的干扰[1]。椒盐噪声是在图像从传感器到传输信道，再到图像解码处理这一过程中产生的像椒盐一样的黑白噪声点。它的存在恶化了图像的质量，影响了人们对图像的观察与研究。严重被噪声污染的图片会淹没图片本身的特征，使图像失去原本保存的意义。因此，图像去噪是图像处理中的一个必不可缺的步骤[2]。

在去除椒盐噪声中，人们首选的方法就是经典中值滤波[3]。1971年，J.W.Tukey提出了中值滤波（median filtering）的概念。中值滤波拥有极好的脉冲噪声抑制能力，在抑制噪声的同时还能注意保护图像边缘信息且易于实现，这使得中值滤波在在图像处理领域中广受欢迎。然而它的缺点就是计算速度不够快，容易丢失图像中一些尖锐的细节，比如折线、拐角等。关于如何更好地去噪，国内外大量学者进行了研究，如R.K.Brownrigg提出的一种加权中值滤波器，Nieminen提出的一种多水平中值滤波器等，然而如何将中值滤波应用到实时传输中还很少有方案。 本文通过建立一种双排序中值滤波算法，不仅能使计算速度更快，同时通过设立阈值能较好地保护图像细节，达到图像实时传输的目的。

1 经典中值滤波

经典中值滤波器的窗口有很多种，如方形窗、十字窗、圆形窗等，不同的窗口可以对不同图像的内容和要求进行处理[4]。其中，对于图像存在尖锐顶角的物体，十字窗窗口处理的效果比较好；而对于外轮廓线比较长的图像，方形窗和圆形窗能达到更好效果地滤波[5]。本文研究的目标是生活中较普遍、应用较广泛的图像，因此本文选择方形窗来处理中值滤波算法。假设一幅灰度图像的部分数据如图所示，中值滤波的滤波方式如图1所示。

图1 经典中值滤波原理

中值滤波的方式是将方形窗中的灰度数据由小到大的顺序进行排列[6]，在3×3方形窗中，中值为排序后9个灰度值中最中间的灰度值[7]。数据9为灰度值极端不同的椒盐噪声，在中值滤波进行大小排序的过程中，椒盐噪声这种极端数据会被集中到左端或者右端，不会作为中间值被选中，通过这种方式就可以将椒盐噪声消除。

中值滤波的方形窗分为3×3、5×5和7×7等，对于处理一幅256×256的灰度图像，选择过大的窗口会导致图像模糊，同时也会占用更多的硬件资源占用更多的时间。本文选用的是3×3方形窗对图像进行处理。

2 改进的中值滤波算法

2.1 双排序中值滤波

经典中值滤波算法在硬件实现中比较耗费时间，不利于进行实时传输[8]，因此，本文提出一种通过改进方形窗中像素灰度值的方法，即双排序中值滤波，来使中值滤波能够更快地完成。相对于传统中值滤波算法，双排序中值滤波的计算时间大大减少，所占用FPGA的资源也较少，它对图像的处理速度更快更便于进行图像的实时传输。

2.1.1 算法原理

在3×3方形窗中，双排序中值滤波先对方形窗中的9个像素灰度值Xi,j进行行排序。即将3×3方形窗的每一行进行从小到大的顺序排列得到X'i,j(X'i,j+1≥X'i,j)，再对X'i,j的每一列进行由小到大的排序得到X'i,j(X'i,j+1≥X'i,j)，其中，i,j∈{1,2,3}。再对X''i,j的对角线取中值输出，即M'=Med(X''1,3，X''2,2，X''3,1)。双排序中值滤波的实现过程如图2所示。

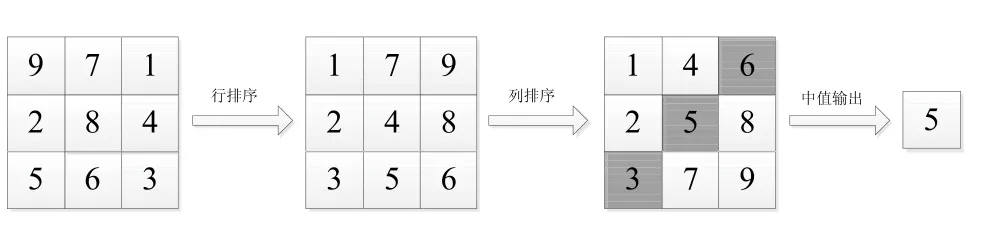
图2 双排序中值滤波算法

2.1.2 算法分析

双排序中值滤波在逻辑上较难理解，下面证明双排序中值滤波的正确性，如图3所示。

图3 算法分析

如图，R1～R9为模板中9个不相等的像素灰度值，首先对这个9个像素进行从小到大的行排序，易得Min(i)＜Med(i)＜Max(i)，其中i∈{1,2,3}。在进行列排序后，易得x1＜x2＜x3，x∈{r,s,t}，r(i)＜s(i)＜t(i)，i∈{1,2,3}。在双排序后，可知t3=Max(max1,max2,max3}，r1Min{min1,min2,min3}。即经过双排序后，t3为9个像素中的最大值，而r1为9个像素的最小值。对于s1来说，s1＜s2＜s3，s1＜t1，s2＜t2，s3＜t3，s1至少小于s2，s3，t1，t2，t3五个像素灰度值，由对称性来看，s3也至少大于五个像素的灰度值，因此，s1和s3也一定不是中值。r2＜s2＜t2，r2＜r3，s2＜s3，t2＜t3。因此r2至少小于s2，t2，r3，s3，t3五个像素灰度值，同理t2也至少大于五个像素的灰度值，因此，r2和t2也一定不是中值。当9个灰度值按从小到大的顺序排列时，r1排在第一位，s1和r2在第二位到第四位之间，s3和t2在第六位到第八位之间，t3排在第九位。在剩下的t1，s2和r3中，其中一个值在第二位到第四位之间，一个值为中值，一个值在第六位到第八位之间，则med=Med{t1,s2,r3}。

由以上数学证明过程上来看，双排序中值滤波是完全正确可行的。双排序中值滤波并没有像经典中值滤波将9个像素灰度值按顺序排列，而是经过几次简单的数据比较运算快速地得到方形窗内的中值。中值滤波算法的硬件实现已经趋于成熟[9]，双排序中值滤波需要对比较器模块进行相应的修改即可实现。

2.2 基于阈值的中值滤波

经典中值滤波的最大缺点就是噪声被消除了，而图像细节却未能得到有效的保护[10]。在经典中值滤波中，图像的非噪声区域也需要进行一次滤波处理，这就可能导致原本数据的改变，从而导致图像细节的丢失。如图4所示。

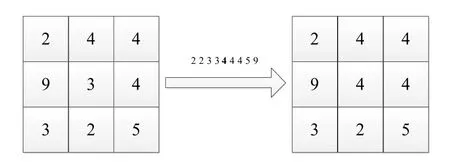
图4 中值滤波的缺点

图像中原本的像素3经过中值滤波处理后变成了4，这就是中值滤波后所造成的细节损害。根据椒盐噪声的较为极端的灰度值特性，本文采取的方法是设立一个阈值鉴别噪声点，在方形窗像素灰度值大于某一阈值或小于某一阈值时，即可定义为噪声点从而进行中值滤波处理，否则将保持原点输出。为最大化地保护图像细节，在大量文献进行的研究中，将灰度值为0的点和灰度值为255的点设置为噪声，便可很好地保护图像细节。该方法在硬件上也很容易实现，只需设定一个条件语句，当图像像素灰度值符合噪声点，则取双排序中值滤波得到的中值代替原数据，否则将保持原值。这种方法并不需要占用过多时间，符合本文图像实时传输的要求。

3 算法分析

3.1 计算速度分析

在经典中值滤波中，计算中值时需要将方形窗内的数据进行逐一比较排序，并以中间值来代替方形窗内的中心值。这需要进行大量的计算，占用更多的硬件资源。对于n个数据，将其进行排序共需要次)比较运算，对于3×3方形窗来说共需要36次运算[11]。可以看出，要对一幅256×256的灰度图像进行经典中值滤波，所耗费的时间还是比较长的。

而在本文提出的双排序中值滤波算法中，采取的时每3个像素灰度值一组的排序算法。进行一次行排序，每行需要进行3次运算，3行共需要9次运算。进行列排序时，同样需要9次运算。最后在三个对角线数据中取中值，则需要3次运算。双排序中值滤波每次方形窗运算共需21次，这比传统中值滤波要节约将近40%左右的时间。

两者相比，双排序中值滤波比传统中值滤波计算更简单，用时更短，这不仅更利于图像的实时传输，也占用了更少的硬件资源，便于用硬件进行实现。

3.2 细节保护分析

目前，在数字图像处理领域对图片的评价尚未有严格统一的标准，通常对图像的评判方法是采取主观评价并辅以客观评价参数[12]。本文采用的参数为归一化均方误差（NMSE）和峰值信噪比（PSNR）。NMSE是常见的衡量图像质量的方法。其值越小，表示图像细节更丰富，更接近原始图像。PSNR与NMSE不同，PSNR的值越小，表示其图像质量越好，其计算公式如下：

其中，g(x,y)是原始输入图像，f(x,y)为去噪后输出图像。M和N表示图像的大小，本文M值和N值都为256。

3.3 结论

在Matlab仿真中，经典中值滤波与本文算法的对比图如图5所示。

可以看出，相比于传统中值滤波，该方法可以对大部分细节进行保护，比如头发等细条更清晰，并且去噪效果也比传统中值滤波更好。NMSE与PSNR数据对比如表1所示。

图5 图像对比

4 结束语

本文对经典中值滤波算法进行了相应的改进，提出了基于阈值的双排序中值滤波算法，这不仅提高了算法计算中值的速度，同时也进一步地保护了图像的细节。随着人类的社会越来越趋于信息化，图像的实时传输将会得到更广阔的发展空间[13]，本文算法可以在占用较少硬件资源的基础上更方便地在FPGA、DSP、GPU等硬件上实现，这为如何使图像进行更快更好地进行传输提供了新的思路。然而由于时间和条件的限制，本文只是验证了该算法的正确性和实用性，如何设定阈值使图像质量最优化，如何在硬件上进行相应的实现将在后续的学习过程中进行不断地探究。

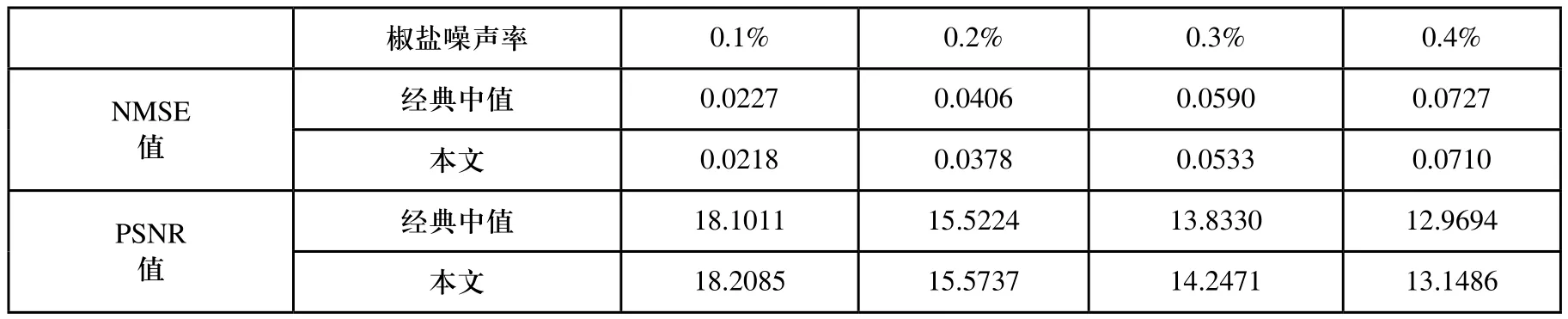
表1 数据对比