浅析两大类型的复合方程及其解题策略
2018-07-21江苏
江苏
常 莲
(作者单位:江苏省常州市前黄高级中学国际分校)
浅析两大类型的复合方程及其解题策略
江苏
常 莲
以复合方程为载体的问题一直是高考的一大热点.这类复合方程问题有效考查了函数与方程、数形结合、转化与化归、分类讨论等数学思想,同时考查了学生作图、计算与逻辑推理等综合能力,进而能够很好地提升数学核心素养.一般地,设y=f(u),u=g(x),当x在u=g(x)的定义域Dg中变化时,u=g(x)的值在y=f(u)的定义域Df内变化,因此变量x与y之间通过变量u形成的一种函数关系,记为y=f(u)=f(g(x))称为复合函数,其由外函数y=f(u)和内函数u=g(x)复合而成.其中x称为自变量,u为中间变量,y为因变量(即函数).
根据复合函数的定义,我们把形如“关于x的方程f(g(x))=m(m为实常数)”称为复合方程,其由外方程f(u)=m和内方程u=g(x)复合而成.下面主要介绍复合方程中的两大类型及解题策略,使学生较好的掌握两大复合方程的类型以及相应的解题策略,教师在教学中可以不断地渗透数形结合、转化与化归等数学思想,从而较好的提高学生的数学核心素养.
一、同种复合方程迭代
“f(f(x))=m”型复合方程,其由外方程f(u)=m和内方程f(x)=u复合而成,内方程和外方程都是采用同一个对应法则,研究这类复合方程的根的情况,通常可以引导学生按照由外而内原则思考,流程如下图:
外方程f(u)=m根的情况
研究函数y=f(u)与函数y=m的图象的交点情况
由m的情况,确定交点坐标中u的取值情况
研究方程f(x)=u根的情况
研究函数y=f(x)与函数y=u的图象的交点情况
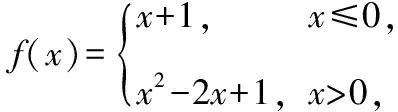
【解析】令f(x)=u,
∴原方程可化为f(u)=m恰有5个不同的实数解,
将研究方程f(u)=m根的情况转化为研究函数y=f(u)与函数y=m的图象的交点情况.
综上,0 【解析】令f(x)=u, ∴原方程可化为f(u)=-1有4个不同的实数解. 【评注】因为同种复合方程的内方程和外方程采用同样的对应法则,所以解题时共用的是同一个函数y=f(x) 的图象,此时正确作图与理解图象就显得至关重要,然后充分利用数形结合进行分类讨论,合理地建立分类标准,问题就会迎刃而解. “g(f(x))=m”型复合方程,其由外方程g(u)=m和内方程f(x)=u复合而成,内方程和外方程采用不同的对应法则,笔者研究此类复合方程发现,除了采用由外而内原则,多数内方程f(x)=u的根的情况确定,此时可以引导学生按照由内而外原则思考,流程如下图: 【解析】令f(x)=u∈R,∴2u2+2bu+1=0恰有8个不同的实数解. 综上,实数k的取值范围为(0,+∞). 【评注】因为外方程是二次方程的复合方程,所以教师在讲解此类题时,应该充分运用二次方程根的判别特征,进一步转化为二次函数的零点分布问题. 【解析】令f(x)=u,u∈(-∞,1],则g(u)=m, 【变式】已知函数f(x)=sinx,g(x)=3x2-x, 若方程g(f(x))=m在x∈[0,2π]上有两个不同的实数根,求实数m的取值范围. (作者单位:江苏省常州市前黄高级中学国际分校)


二、不同种复合方程迭代
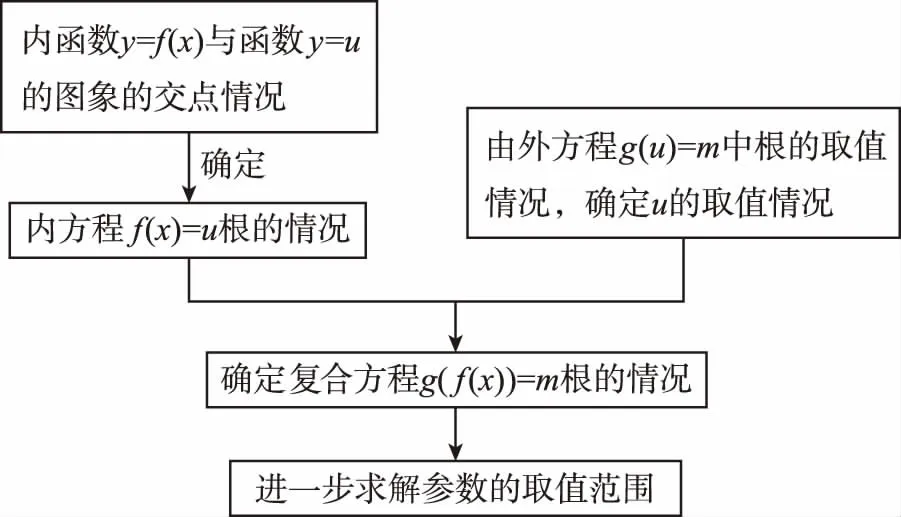
1.“af2(x)+bf(x)+c=0”型复合方程,外方程是二次方程



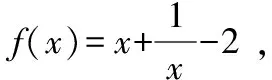

2.“f(g(x))=m”型复合方程,外方程不是二次方程






