精设题组 八大途径破解圆锥曲线离心率范围

广东

温伙其

(作者单位：广东省广州市第十六中学)

精设题组 八大途径破解圆锥曲线离心率范围

广东

温伙其

离心率是圆锥曲线重要几何特征之一，各种教材都会详细介绍，但对离心率范围问题甚少阐述.近年高考全国卷对离心率的取值范围的考查已成为高频考点和重点.本文通过设置题组的形式，归纳了八种常见解决离心率取值范围的途径，探讨解题的思路与要点，供读者参考.

题组一 函数法，即构造离心率的函数关系式，借助值域求范围

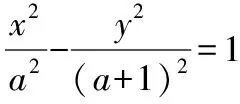
【解题分析】

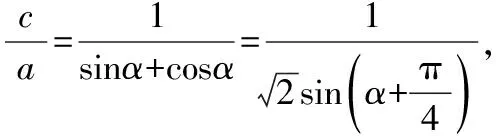
【解题要点】

1.根据题设条件，如曲线的定义、等量关系等建立离心率和其他一个变量的函数关系式；

2.确定函数的定义域及单调性；

3.利用函数求值域的方法求解离心率的范围.

题组二 角度法，即借助角的大小(钝角、锐角、直角)构造a,b,c齐次不等关系

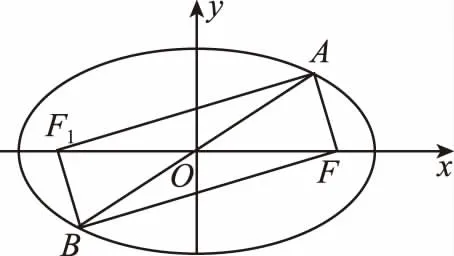
1.如图，椭圆的中心在坐标原点O，顶点分别为A1，A2，B1，B2，焦点分别为F1，F2，延长B1F2与A2B2交于P点，若∠B1PB2为钝角，则此椭圆的离心率的取值范围是________．

【解题分析】

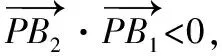
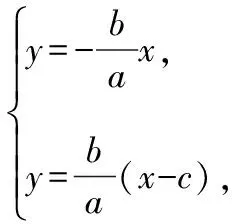
【解题要点】

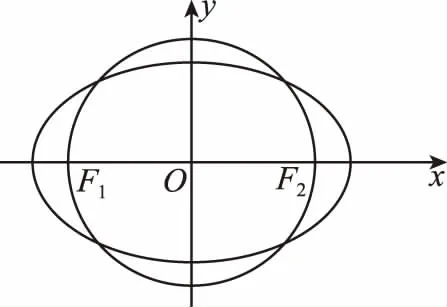
1.钝角可得向量的数量积大于0；

2.锐角可得向量的数量积小于0；

3.直角三角形则有直角边小于斜边；

4.根据上述大小关系整理为关于a,b,c的齐次不等式，转化为离心率的不等式.

题组三 条件法，即借助条件的不等关系，构造a,b,c的齐次不等式

【解题分析】

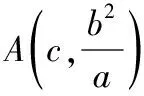
【解题要点】

1.找出题目本身给出的不等条件，如已知某些量的范围，线段的长度，面积的取值等；

2.把上述的量用a，b，c表示；

3.整理得离心率的不等关系式，从而求解.

题组四 三边大小法、均值定理法和性质法，构造a,b,c齐次不等关系

【解题分析】

【解题要点】

1.三角形两边之和大于第三边，三角形两边之差小于第三边；

4.把上述大小关系整理为关于a,b,c的齐次不等式，转化为离心率的不等式.

题组五 图象法，即借助特殊图象特征构造a,b,c齐次不等关系

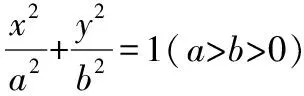
【解题分析】

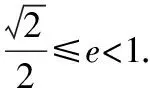
【解题要点】

1.圆和圆锥曲线的交点数量问题，即为它们的位置关系问题，作图可寻找a，b，c和半径大小的关系；

2.直线和双曲线的交点问题，即为它们的位置关系问题，作图可得的直线斜率和渐近线斜率大小的关系；

3.把上述大小关系整理为关于a,b,c的齐次不等式，转化为离心率的不等式.

题组六 有解成立法，即把存在性(有解)和恒成立问题转化为函数最值

1.题目同题组五第1题.

【解题分析】

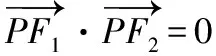
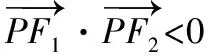
【解题要点】

1.函数m=f(x)有解，即不等式f(x)min≤m≤f(x)max成立；

2.函数m≥f(x)恒成立，即不等式m≥f(x)max成立；

3.函数m≤f(x)恒成立，即不等式m≤f(x)min成立；

4.把上述大小关系整理为关于a,b,c的齐次不等式，转化为离心率的不等式.

题组七 位置关系法，即利用点在曲线内(外)部建立离心率不等式

【解题分析】

【解题要点】

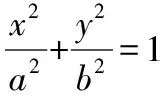
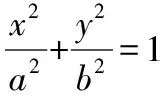
3.把上述大小关系整理为关于a,b,c的齐次不等式，转化为离心率的不等式.

题组八 判别式法，即转化为a,b,c齐次方程解的数量问题

1.题目同题组五第1题.

2.题目同题组七第2题.

【解题分析】

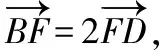
【解题要点】

1.直线与圆锥曲线的交点问题，联立方程后，转化为一元二次方程的求判别式问题；

2.直线与双曲线的交点在同一支(在不同的两支)问题，转化x1·x2的符号问题；

3.把上述问题整理为关于a,b,c的齐次不等式，转化为离心率的不等式.

(作者单位：广东省广州市第十六中学)