“不等式解法及其应用”复习策略探究

甘肃

董 强

(作者单位：甘肃省陇南市西和县第一中学)

“不等式解法及其应用”复习策略探究

甘肃

董 强

不等式是刻画现实世界中不等关系的重要数学模型，是进一步学习数学和解决其他数学问题的基础和有利工具.现行各版本高中教材中，除选修4—5“不等式选讲”外，只在必修5第三章“不等式”与选修1—2(文)、选修2—2(理)第二章“推理与证明”中涉及不等式相关内容.纵观近几年高考试题对解不等式问题的考查，主要涉及指数不等式、对数不等式、绝对值不等式、分式不等式、一元二次不等式等，且多与函数、数列、圆锥曲线、概率、向量等综合考查，解题时从函数性质，如函数的单调性、奇偶性及3个二次关系等入手，便可找到问题的突破口，从而快速解题.

一、巧用不等式的性质转化求解

不等式的性质是求解不等式的重要方法之一，将一些待求解的不等式通过不等式的性质转化为一元二次不等式、分式型不等式、绝对值不等式等常见类型进行求解往往是解不等式的重要途径.

(一)一元二次不等式的解法

【例1】(2015·江苏卷·7)不等式2x2-x<4的解集为________.

【答案】(-1，2).

评注：首先将指数式化为一元二次不等式x2-x-2<0，再求解.一元二次不等式、一元二次方程以及所对应的二次函数关系密切，即一元二次方程的两个根(Δ≥0)正好是所对应二次函数图象与x轴交点的横坐标，也恰是一元二次不等式解集的“分界点”.所以求解一元二次不等式一般要与一元二次方程和二次函数的图象紧密关联，首先对不等式进行变形，将不等号一端二次项系数化为大于0，另一端为0，即化为ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0)的形式，再计算相应的判别式Δ，当Δ≥0时，求出相应的一元二次方程的根，最后根据对应的二次函数的图象，写出一元二次不等式的解集，当Δ<0时，结合二次函数图象写出所对应一元二次不等式的解集．

(二)分式型不等式的解法

( )

【答案】A.

评注：分式型不等式求解时首先应通过移项将右边化为0，再根据符号法则“同号得正，异号得负”的原则进行分类讨论，将分式型不等式化归为整式型不等式(组)进行求解，注意转化过程的等价变形，对小于等于及大于等于0型的分式不等式在变形为整式不等式后，应去掉使得分母等于0的值．含有两个因式的分式型不等式都可以化归为一元二次不等式进行求解，对于含有多个因式的分式型不等式求解时还可以使用“穿针引线”的方法.

(三)绝对值不等式的解法

绝对值不等式是高考的重难点之一,求解此类题目的关键在于如何去掉绝对值符号,进而转化为常见不等式,简化运算.

【例3】(2016·全国卷Ⅰ理·24)已知函数f(x)=|x+1|-|2x-3|.

(Ⅰ)在图中画出y=f(x)的图象；

(Ⅱ)求不等式|f(x)|>1的解集.

评注：对含有绝对值的不等式的求解一般采用零点分段讨论法，单绝对值一般分两类去绝对值，双绝对值一般分三类去绝对值，求解形如|x-a|±|x-b|≥c的不等式时先求两个绝对值的“零点”，再划分区间，分类去绝对值符号，分别解去掉绝对值后的不等式，最后对三类结果求并集，即为原不等式的解集，应特别注意区间的端点值.另外，对含有绝对值的不等式求解时，还可以利用绝对值的几何意义，由于|x-a|+|x-b|与|x-a|-|x-b|分别表示数轴上与x对应的点到与a，b对应的点的距离之和与距离之差，因此对形如|x-a|±|x-b|c(c>0)的不等式，利用绝对值的几何意义求解更直观.如本题也可以先画出y=|f(x)|的图象以及直线x=1，然后根据图象写出解集.

二、利用函数的性质求解不等式

(一)利用函数的单调性

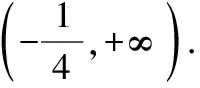
评注：可以采用分段函数分类讨论的思想，结合函数的单调性求解不等式，单调性是函数的重要性质之一，和不等式的关系极其紧密，充分利用函数的单调性解不等式是数学核心素养的重要体现.

(二)利用函数奇偶性求解不等式

【例5】(2010·课程标准卷理·8)设偶函数f(x)满足f(x)=x3-8(x≥0)，则{x|f(x-2)>0}=

( )

A.{x|x<-2或x>4} B.{x|x<0或x>4}

C.{x|x<0或x>6} D.{x|x<-2或x>2}

【答案】B.

评注：根据偶函数的性质，结合函数的图象，将不等式的求解转化为函数零点的求解问题，通过数形结合，直观地看出所要求解不等式的解集，这是利用函数的性质求解不等式的巧妙之处.

三、不等式的基本应用

(一)基本不等式在解决实际问题时的应用

【例6】(2017·江苏卷·10)某公司一年购买某种货物600吨，每次购买x吨，运费为6万元/次，一年的总存储费用为4x万元，要使一年的总运费与总存储费用之和最小，则x的值是________.

【答案】30.

(二)不等式在线性规划中的应用

【例7】(2016·全国卷Ⅰ·文理16)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg，乙材料1 kg，用5个工时；生产一件产品B需要甲材料0.5 kg，乙材料0.3 kg，用3个工时. 生产一件产品A的利润为2 100元，生产一件产品B的利润为900元.该企业现有甲材料150 kg，乙材料90 kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为________元.

【答案】216 000.

评注：利润最大、效益最高、材料最省、花费最少等实际问题往往涉及线性规划的知识，线性规划是每年高考必考的内容，多以选填题的形式出现，基本题型有给出约束条件求目标函数的最值，通过目标函数的最值确定相应参数的值，通过实际问题背景蕴含线性规划知识等.线性规划一般有纵截距、斜率、两点间的距离、点到直线的距离等命题视角,解决此类问题常利用数形结合的思想.本题先将实际问题转化为线性规划问题，再利用线性规划的知识进行求解.

(三)三角形不等式的应用

评注：绝对值三角不等式在求解双绝对值不等式的最值问题时具有快速、简洁的特征，尤其是向量形式的三角不等式更具明显的几何意义，即“三角形的两边之和大于第三边，两边之差小于第三边”.

四、有关不等式复习策略的教学建议

(一)立足课本，强化基础

“立足课本”是“不等式”教与学的归宿，重新解读教材，激活已学知识，清晰课本中各概念的内涵与外延，注重课本知识的内在联系，传承教材结论，总结思想方法，将课本中的有关不等式的性质的来龙去脉、各种变式熟练掌握，强化不等式学习的理论基础，能够根据不等式的相关性质进行不等式的求解、探索与证明，这是不等式学习必须注意的一个方面.

(二)瞄准高考，注重通法

高考试题中有关不等式的求解类题目都是一些比较重要的、常规的不等式，对这些不等式的求解必须要注重通性通法，如上述的一元二次不等式、分式型不等式、绝对值不等式等的求解，都有着一般的“套路”，这些通法的学习是不等式求解中非常关键的环节. 通性、通法是解决不等式相关问题的根本方法，不偏、不难、不怪，而运用函数的性质解不等式等是区分学生是否具有较好数学素养的重要指标.

(三)巧妙转化，融会贯通

含参数问题，不等式恒成立问题，与数列、函数结合的不等式问题常常出现在高考的压轴题中，是区分学生是否能得高分的重要部分，对这些试题中不等式的求解一定要审时度势，审题时把题目中的疑点、难点、关键点找出来，当解题遇到障碍时，利用其他知识将不等式的求解问题巧妙转化，做到不同知识点的融会贯通，如构造函数、分离参数等可以将不等式求解转化为函数，利用函数的相关性质、函数的图象等巧妙解题.

(四)构建模型，重视应用

(作者单位：甘肃省陇南市西和县第一中学)