例析背景下的解析几何问题
2018-07-21广东
广东
刘光明
(作者单位:广东省汕尾市华南师范大学附属中学汕尾学校)
广东
刘光明

一、离心率问题
离心率问题是高考解析几何中的常见问题,其核心是寻找a与c之间的关系,通常都是根据已知条件构造方程或分别求出a,c的值.
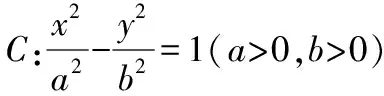


二、直线问题
直线问题无非就是直线斜率或者直线方程的求解,在解析几何中直线作为与曲线相交的主要角色,常常设直线的点斜式或者斜截式,当然通过几何图形分析直线斜率也不失为一种高明之选.
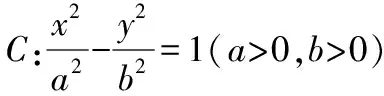
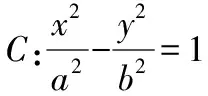

【例题3】(2009·全国卷Ⅱ理·9)已知直线y=k(x+2)(k>0)与抛物线C:y2=8x相交于A,B两点,F为C的焦点,若|FA|=2|FB|,则k=
( )



【点评】与抛物线焦点相关问题,利用抛物线的定义,借助几何图形分析,将数形结合思想融入解题之中.
三、轨迹问题
处理轨迹方程问题常见的方法有直接法、定义法、相关点法、待定系数法等,在解析几何中轨迹方程作为后续问题的基础,正确求解方程有着至关重要的作用.
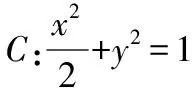
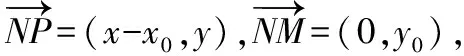



四、弦长问题

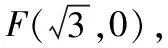



五、取值范围与最值问题
取值范围问题在考试中难度要求都不低,首先要将要求范围的代数表达式求解出来,然后借助不等式或者函数的值域处理,当然特殊值或者特殊图形对于范围估计也有一定的帮助. 解析几何中,图形上的动点设置条件确定某字母的取值范围.
【例题7】(2016·四川卷理·8)设O为坐标原点,P是以F为焦点的抛物线y2=2px(p>0)上任意一点,M是线段PF上的点,且|PM|=2|MF|,则直线OM的斜率的最大值为
( )


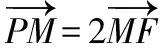
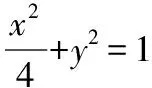

从上述例题的阐述中,可以得到以下几点启示:(1)在解析几何的教学中,需要重视各种曲线的定义辨析,舍得花时间与学生一起认真审题,逐条“翻译”题中的每一句话,让学生清晰地知道解析几何分析的大致程序;(2)关注解析几何中“设而不求”和“几何关系”两种意识的培养,加强学生运算能力的引导,教师多示范性地演示计算详情,培养学生良好的计算习惯;(3)关注删除几何证明选讲后引起的蝴蝶效应,解析几何实质也是几何的一份子,利用几何图形分析数学问题是数形结合思想的完美呈现,有助于提升学生直观想象素养.

(作者单位:广东省汕尾市华南师范大学附属中学汕尾学校)
