浅谈椭圆的概念在数学本质下的教学研究

□海南省海南中学 唐盛彪 叶 穗

数学概念作为教学中的重要环节，是数学知识体系和思想方法的奠基之石和重要载体。在教学过程中，应引导学生参与概念的形成和发展的过程，深入探究概念的深层内涵，剖析其数学本质，展示隐含其中的数学思想方法，感悟数学特有的数学思维方式，帮助学生更好地理解数学概念，达到有效教学。

圆锥曲线的内容尤其椭圆在高中数学中要求较高，其概念教学又是重点教学之一，但因其教学上的不当设计，常造成学生在概念上形成断层，思维模式固化，未深入了解椭圆便开始投入到大量的题海战术中，但又无从下手。在目前的教学现状中关于椭圆的定义呈现出概念引入和标准方程的推导过程被严重忽视现象，多数教师基本就是举几个生活中的例子，再形式化类比圆的画法，利用一个绳子固定两定点直接画出椭圆，椭圆的定义未经仔细打磨便呼之而出，随后用几句话说明如何建系，便开始了复杂的公式推导过程。有心的教师在引入上下足了功夫，提到了椭圆作为圆锥曲线的来源，但因为概念教学中严重脱离了剖析数学本质的过程，概念教学仅起到擦边球的效果。而如何基于数学本质进行概念教学，是需要我们不断地在教学实践中学习和总结的。

2017年9月，我校数学组组织了一次组内公开课，笔者在此次活动中，以人教A版数学选修2-1第二章第二节《椭圆的标准方程》为课题上了一节基于数学本质的数学概念生成课，以探究如何进行有效的椭圆概念教学。

一、教材分析

《椭圆的定义及其标准方程》选自高中数学人教A版选修2-1的第二章《圆锥曲线与方程》的第一节。作为本章节的一个重要知识点，是除了圆以外又一个以“代数方法研究几何问题”解决曲线问题的实例，深度剖析了利用圆锥曲线方程研究圆锥曲线几何性质的方法，为后面进一步研究双曲线、抛物线提供了基本的研究模式和方法。

由于椭圆的定义是通过描述椭圆形成的过程中得到的发生性定义，较其他数学定义比较特殊。又因其形象在生活中处处可见，学生对椭圆已有了一定的感性直观认知，同时也初步掌握了一些简单研究解析几何的思维方法，但对椭圆数学化的描述和研究仍然是模糊的，教学中应注重的是椭圆本质是什么以及如何研究它的性质，而不是教学方式和教学流程。数学本质的体现主要在数学知识的发生、形成、性质、应用几方面，同时因为数学的严谨性和复杂性，教学中强调渗透的本质也要与学生的认知水平能力相符合，从而达到教学效应最大化。

根据本节内容的特点，笔者认为，椭圆概念的形成若要体现其数学本质，必然要学生亲身经历概念自然形成的过程。从基本实验入手，动手操作，教师合理提问，归纳总结，深入概念内部进行研究，彻底解决学生对椭圆概念的疑惑，达到学生对椭圆定义及其标准方程的发现和理解的目标。这就需要充分发挥信息技术的作用，为学生的数学探究与数学思维提供支持，培养学生的数学实践能力和创新精神。

二、教学实录

1.创设情境，引入课题。

情境1：利用多媒体课件展示生活中与椭圆有关的图形，让学生观察太阳系当中各个行星的运行轨迹，以及鸟巢的俯视平面形状，描述都是什么曲线？并举例说明。

情境2：装了半瓶水的圆柱形水瓶，正常放置的时候，水平面边界线是圆，倾斜放置的时候，水平面边界线是椭圆。

将水瓶的形状换成圆锥（几何画板演示），利用平面切割圆锥，分别得到了圆、椭圆和双曲线，解释椭圆为何被称为圆锥曲线的由来。

教师提问：椭圆到底从数学的角度，应如何下定义？椭圆的性质如何研究？

【设计意图】椭圆概念的引入，情境1：数学来源于生活，利用生活中的材料让学生直观感受椭圆的形状，使学生对椭圆初步产生一种感性认知。情境2：数学服务于生活，从生活回归数学，抽象为平面切割圆锥而得到圆锥曲线。两个情境都为后面学生理性认知椭圆作了合理的过渡。

2.探究实验，形成概念。

（1）椭圆定义探究

教师：回顾与椭圆相似的闭合曲线——圆的定义和画法。是否可以类比圆的画法画出椭圆。（类比过程中，应抓住两个关键点，定点和定长。）

分组实验1：其中一组将一条定长的细绳两端固定在两个定点上，用笔尖勾直绳子，使笔尖移动。另外几组根据其他猜想画图，例如利用一个定点和两个定长直线画图或其他猜想。各组观察画出的图形。

通过实验，学生发现只有利用两个定点和一个定长的直线，笔尖的轨迹才是椭圆，且笔尖到两个定点的距离之和为直线的长度。

教师：请简单总结椭圆定义（模仿圆定义的描述类比给出椭圆定义）

（大部分）学生答：到两定点距离的和等于常数的点的轨迹是椭圆。

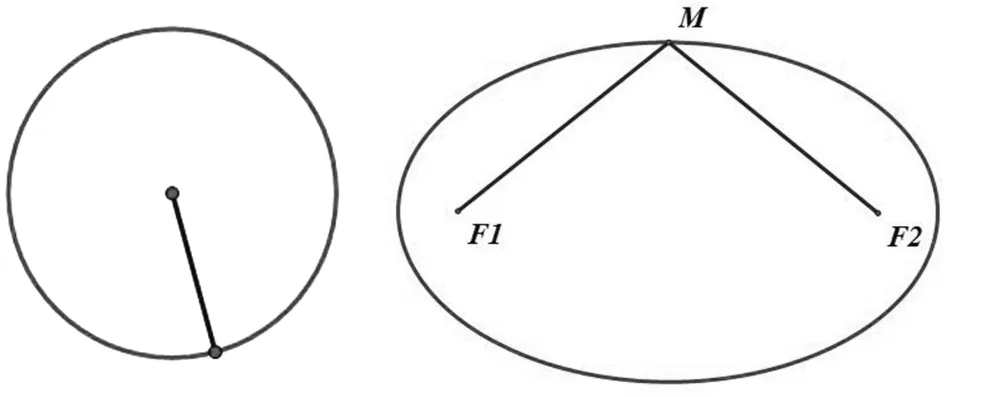
（多媒体展示）

【设计意图】类比圆的画法探究椭圆的画法，但类比不能落入形式化，直接给出结果限制了学生的思考，分组让学生自己先猜想，再动手试验，让学生对概念的形成有个逐渐认知的过程，提高学生探究的兴趣。

（少部分）学生疑问：所有的椭圆都是这么画出来的吗？有没有比较特殊的椭圆不满足这个条件呢？

实验2：学生课前已准备好圆形纸板或纸片，引导学生在纸片上随意选取一个点（除去圆心），记为点，然后依次从边缘开始进行折纸，折起的圆弧都要经过点，经过多次折纸之后，将会得到若干条折痕，让学生观察折痕包围的图形。学生通过实验发现折痕包围的图形边缘是椭圆。

（利用几何画板演示折纸过程）

教师：折纸的原理是什么。该椭圆是由哪些点构成的？

学生：定点P和圆周上的点N关于折痕对称，椭圆是和折痕ST的交点M的轨迹。

教师引导学生同时观察到|MA|+|MO|=|ON|=圆的半径（定长）

演示：选取任意一个椭圆进行验证。（几何画板展示验证过程）

随便取一个椭圆，移动椭圆上的点，椭圆上的点到两个定点的距离恒为定长，改变椭圆形状，该性质保持不变。

因此所有的椭圆都可以通过这个方式画出来。

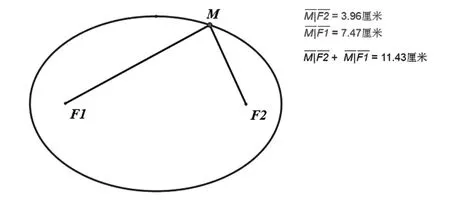
【设计意图】有些学生难免产生疑问，就问随手画出的椭圆会不会是巧合，或者个别椭圆不满足这样的条件呢，这样验证之后，学生对这个画法的合理性就有了更深刻的认识。

2.归纳提升，完善定义。

教师：到两定点距离的和等于常数的点的轨迹是椭圆，这个定义是否需要补充，或有什么限定条件？

学生：（一时答不上来，觉得这个概念相对完美了）

实验3笔尖不仅在两个定点所在的平面上移动，还在空间中移动，观察笔尖的轨迹（确保定义的前提是在平面内）

【设计意图】一开始看，学生给出的定义似乎非常合理，但其实存在着很多漏洞，引导他们深入挖掘，解惑的过程让学生对这个概念的理解和认识会加深很多。

教师：将椭圆定义翻译成数学语言，设两定点分别为F1、F2，绳子的定长为2a，常数|F1、F2|≥2a是一个重要的量，此时轨迹还是圆吗？

利用多媒体课件演示，同时让学生归纳。

|MF1|+|MF2|＞|F1、F2|椭圆

|MF1|+|MF2|=|F1、F2|线段

|MF1|+|MF2|＜|F1、F2|不存在

教师：请同学们完善椭圆的定义。

（板书）：平面内到两个定点F1、F2的距离的和等于常数（大于|F1、F2|）的点的集合叫做椭圆。其中这两个定点叫做椭圆的焦点，两个焦点间的距离叫做椭圆的焦距。

【设计意图】椭圆的定义初步的给定，学生并未能一下子考虑到焦距和定长之间的关系影响了轨迹的形状，简单的一句话也揭示不了椭圆定义的本质。经过引导之后，刺激了学生继续往下思考，从而将概念补充完整，也让学生体会到了概念的形成要多方面考虑，促使学生养成思考问题的良好习惯。

3.建系设点，化简方程。

思考：回顾求圆方程的方法和步骤，尝试推导椭圆的方程。

第一步：建立平面直角坐标系

方案1：在椭圆上任意选取一点作为原点建系；

方案2：选取两个焦点的其中一个作为原点，以两焦点所在直线为x轴建系；

方案3：以两个焦点的中垂线作为y轴，以两焦点所在的直线作为x轴建系；

…

学生们经过热烈讨论后，根据椭圆的对称性和建系的方便性，选取了方案3，以焦点在x轴上的椭圆为例建系。

第二步：设点F1（-c，0）、F2（c，0），椭圆上的点M（x，y）

第三步：列方程|MF1|+|MF2|=2a

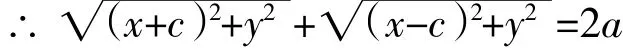
两边再平方化简得（a2-c2）x2+a2y2=a2（a2-c2）

扩展思路：第三步的方程化简也可如下

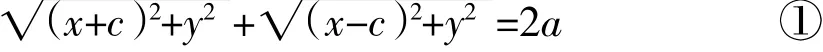
两边同乘根号差得：

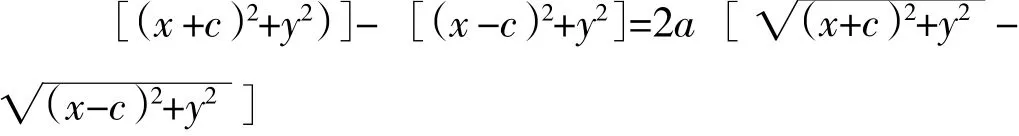
它们的几何意义是动点P（x，y）与定点F2（c，0）（或F1（-c，0））的距离和它到定直线的距离的比是离心率e，常常被称为椭圆的第二定义。

思考：学生猜想焦点在y轴上的椭圆方程的形式，并思考如何利用标准方程判断其焦点位置。

【设计意图】让学生参与到问题的解答中，体验方程推导的全过程，数形结合思想，用代数方法解决几何问题的思想和方法，达到真正掌握这一方法的目的。同时扩展其他标准方程推导的方法。

三、小结

若要深入椭圆定义的本质去进行教学设计，应该先深入剖析教材，体现从图像到数学对象的自然过渡。在概念教学中切忌一味追求所谓的数学本质，应充分考虑学生的接受能力，通过具体对象反映椭圆的本质特征，才能真正上好一堂合格的概念课。