一种新型组合树突形装药设计分析*

2018-07-20蒋雨晴梁国柱

固体火箭技术 2018年3期

蒋雨晴，梁国柱

(北京航空航天大学宇航学院，北京 100083)

0 引言

固体火箭发动机装药的几何形状和尺寸决定了发动机的燃气生成率及其变化规律。因此，也就影响到燃烧室的压强和发动机推力随时间的变化。

常用的传统二维装药几何研究较为广泛，主要有星形装药、车轮形装药和槽形装药等，它们的几何燃烧特性计算方法在一些文献中已详细给出。Roy Hartfield与John E Burkhalter等[1-2]导出了常用的星形装药、车轮形装药(长辐条车轮形与短辐条车轮形)与槽形装药的燃面及通气面积公式，给出了分类条件及相应的约束条件。Andrea Ricciardi[3]给出带有星角圆弧(凸圆弧与凹圆弧两类)的星形装药在应用中的约束条件，分析所有可能出现的情况，得到了各种情况不同燃烧阶段的燃面与通气面积公式。王光林等[4]也给出了星形和车轮形装药燃面与通气面积的计算式和变化规律。

由两种不同结构参数的星角或辐条交替排列得到的装药类型称为树突形装药。树突形装药作为星形装药与车轮形装药的扩展，在文献中鲜有计算方法与分析，仅仅被简单提及优点与结构。Max W Stone[5]提出了改进后的车轮形装药(即树突形装药)，进行了参数简化工作、导出了燃面等参数的计算公式并分析装药优势在于多推力，但仅着眼于两种参数不同辐条交错排列的装药形式，未分析星角与辐条交错排列的形式。Brooks W T[6]简单提到了树突形装药是星形装药与车轮形装药的衍生类型，Roy Hartfield与John E Burkhalter等[1]提及了树突形装药的计算方式，但没有给出计算公式，也没有分析燃烧特性。Arie Peretz[7]分析了一种由改进车轮形装药衍生而来的树突形装药的燃烧特性，虽然分析了所有可能的类型，并给出了燃面与通气面积计算式，但没有涉及星角与辐条交错排列的树突形装药。上述文献提及树突形装药(或改进车轮形装药)，但都集中于辐条交错排列的形式，未对星角与辐条交替排列的树突形装药的研究。因此，对这类装药可能的组合类型、装药燃烧特性与优点无从知晓。

本文提出一种新型组合树突形装药，该装药由星角与辐条交替排列组合而来。首先，分析确定新型组合树突形装药的结构参数；然后，将星角与辐条燃烧分开分析，在等速燃烧的条件下，得到装药各个阶段燃烧周长与通气面积及它们的变化规律。在此基础上，分析比较新型组合树突形装药与星形装药和车轮形装药的装填分数。以本文研究为基础，可进行该装药的内弹道与优化设计研究。

1 新型组合树突形装药原理分析

1.1 装药结构定义

车轮形装药辐条与星形装药星角交替排列，形成一种组合形式装药，称之为组合树突形装药。装药中所有辐条的结构参数相同，所有星角的结构参数也相同。总共有N个单元，沿着各对称轴可将该装药的横截面分成相同的2N份，如图1所示，取其中1份(扇形AOB区域)进行研究。横截面中的10个参数定义如表1和图2所示。

从表1和图2可知，欲将新型组合树突形装药变化为星形或车轮形装药，只需要将相应的辐条或星角角度系数取为0即可。例如，若要变为星形装药，可令ε1=0，辐条便消失，只剩下星角。

分析装药的燃烧周长与通气面积时，为了不引起多余的计算或者遗漏某个部分，需要将星角、辐条和它们之间的过渡圆弧产生的燃烧周长与通气面积分开分析，再将得到的结果相加。

1.2 装药约束条件

在设计星形与车轮形两类装药时，为避免几何上的干涉，同时为排除对工程应用没有意义的结构参数组合，需要对各自的结构参数进行约束。对于本文研究的新型组合树突形装药，需要同时考虑星形与车轮形装药的约束，两者的组合也会带来新的约束条件。

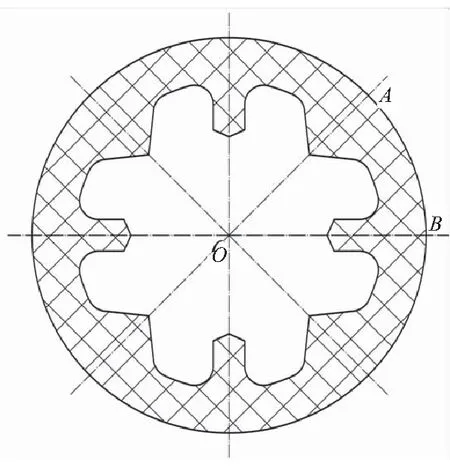
图1 新型组合树突形装药横截面Fig.1 A new kind of combined dendrite grain

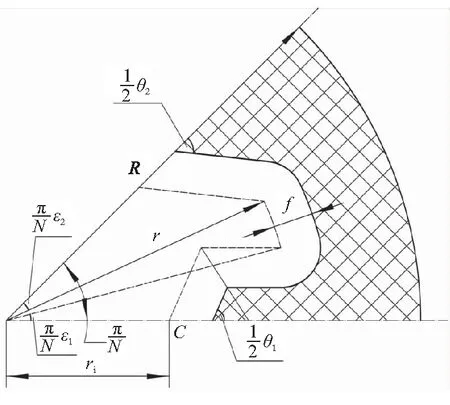
图2 结构参数示意图Fig.2 Definition diagram of structure parameters

表1 结构参数Table1 Structure parameters

对于辐条部分，须保证相邻辐条不交叉。因此，需要满足下列条件：

(1)

为了使辐条能够形成且不与对向辐条交叉，各参数有如下关系式：

(2)

ri≥0

(3)

星角不发生交叉的条件是

(4)

新型组合树突形装药中相邻辐条与星角可能存在交叉现象，为避免这一现象的发生，首先应满足辐条与星角根部不交叉的条件：

ε1+ε2≤1

(5)

为了不出现图3所示交叉情况，需要满足辐条侧端点与星根的连线处于星角边线外侧，即

φ1>φ2

图3 星角与辐条侧端干涉Fig.3 Interference of star and wagon side faces

得出

(6)

本文研究的新型组合树突形装药需要同时满足式(1)～式(6)，且为工程中较常用的情况。

1.3 装药的组合类型

在满足约束条件(1)～(6)的情况下，由结构参数确定得到的新型组合树突形装药将有很多种组合类型，为便于工程设计，选用合适的装药轮廓，需要对可能的装药结构进行讨论。新型组合树突形装药中，星角与辐条互不干涉，两者的结构在装药燃烧过程中相互不产生影响。因此，可对星角、辐条与圆弧过渡段分别讨论，最后进行组合分析，就可得到新型组合树突形装药可能的燃烧情况。星角与辐条每个阶段的燃烧具有不同的特点，不同结构参数时，同一阶段特性相差不大。因此，按照二者的燃烧阶段进行装药类型的划分较为合理。

星角的燃烧分为三个阶段，前两个阶段为装药的主要燃烧过程，其中星角燃烧殆尽的过程为第一燃烧阶段，星角烧尽且主要装药肉厚未燃烧殆尽的燃烧过程为第二阶段，第三阶段为余药燃烧阶段。从星角燃烧开始分别到三个阶段结束的燃烧肉厚如式(7)～式(9)所示，下标数字表示阶段序号：

(7)

webS2=R-r-f

(8)

(9)

辐条部分可以为长辐条或短辐条，它们的计算会有不同之处，短辐条相比长辐条多出了一个燃烧阶段。短辐条的第一阶段为辐条由顶角向根部燃烧殆尽的过程(此时顶角尚未燃尽)，第二阶段为顶角燃尽的过程，第三燃烧阶段与星角第二燃烧阶段相同，余药阶段与星角完全一致。长辐条的第一阶段为辐条由侧面向辐条对称面燃烧殆尽的过程(燃尽时辐条与顶角消失)，其第二三阶段与星角二三阶段一致。短辐条从燃烧开始，到四个阶段燃烧结束，所对应的燃烧肉厚如式(10)～式(13)所示：

(10)

webSW3=R-r-f

(11)

(12)

第二阶段燃烧肉厚需要通过式(13)数值计算得到

(13)

其中

(14)

长辐条从燃烧开始到三个阶段结束的燃烧肉厚表达式如式(15)～式(17)所示：

(15)

webLW2=R-r-f

(16)

(17)

从式(8)、式(11)与式(16)可发现，到星角与辐条余药阶段开始时刻，燃烧肉厚相同。由于余药阶段燃烧规律相同，星角与辐条的燃烧结束时间先后对组合类型没有影响。因此，只有前几个阶段燃烧结束时的燃烧肉厚(webS1与webLW1或webSW1、webSW2)可能存在多种排列情况，表2为新型组合树突形装药组合类型。

表2 新型组合树突形装药组合类型Table2 Combined types of the new kind of combined dendrite grain

1.4 燃烧周长与通气面积

新型组合树突形装药设计需要得到装药燃烧周长与通气面积随着燃烧肉厚的变化关系，该装药由辐条、星角与过渡圆弧三部分组成。计算时，只需要将三部分燃烧周长相加，即可得到研究单元的燃烧周长，通气面积同理计算。由于研究的对象是整个装药横截面的1/2N，其燃烧周长S与通气面积Ap与装药总燃烧周长Stotal与总通气面积Aptotal的关系式为

Stotal=2NS

(18)

Aptotal=2NAp

1.4.1 星角部分燃烧周长与通气面积

图4 星角第一阶段燃烧周长及通气面积Fig.4 Burn perimeter and port area of star segment phase one

图5 星角第二阶段燃烧周长及通气面积Fig.5 Burn perimeter and port area of star segment phase two

星角第一阶段燃烧周长为

(20)

第一阶段的通气面积可表示为四边形ABCD面积与扇形CDE面积之和。

(21)

(22)

其中

(23)

第二阶段的通气面积为ΔABC面积与扇形BCD面积之和。

(24)

图6 星角余药阶段燃烧周长与通气面积Fig.6 Burn perimeter and port area of star segment sliver phase

燃烧周长表达式为

S=(y+f)(β-γ-ξ)

(25)

其中

(26)

(27)

(28)

余药阶段通气面积为ΔADE面积、扇形CAD面积与ABC面积三部分之和。计算ABC面积时，由于它不是扇形，因此用圆心角为μ的扇形BEC面积减去ΔAEC的面积。余药阶段通气面积为

(29)

其中

(30)

1.4.2 辐条部分燃烧周长与通气面积

辐条部分可以为长辐条和短辐条两种类型，它们的燃烧过程与星角相似。其中，长辐条与星角最为相似，除第一阶段不同外，其余阶段都相同，而第一阶段又与短辐条第一阶段计算方式相同。因此，先推导短辐条的燃烧周长与通气面积计算公式，长辐条的计算公式可很快得出。短辐条最后两阶段与星角最后两阶段燃烧规律相同，下面分析短辐条第一与第二阶段。短辐条第一阶段横截面如图7所示。

(31)

其中，H为辐条的半宽度，表示为

(32)

图7 短辐条第一阶段燃烧周长与通气面积Fig.7 Burn perimeter and port area of short wagon segment phase one

第一阶段燃烧的通气面积表示为RTΔADG面积加上扇形BAC面积，再减去半个辐条CDEF的横截面积，表达式如下：

(33)

(34)

其中

(35)

(36)

式(36)中，h的计算式由式(14)给出。短辐条第二阶段燃烧周长为

(37)

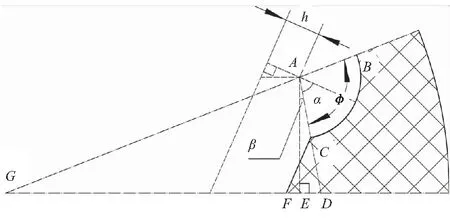
图8 短辐条第二阶段燃烧周长通气面积Fig.8 Burn perimeter and port area of short wagon segment phase two

第二阶段燃烧通气面积与第一阶段类似，表示为RTΔAEG面积加上扇形BAC面积，减去半个辐条顶部面积，即ΔCDF的面积。扇形对应的圆心角变小，因而还需要加上ΔADE的面积。因此，通气面积表示为

(38)

其中

(39)

短辐条第三阶段和余药阶段燃烧周长与通气面积可参考星角第二阶段和余药阶段进行计算，计算时将星角参数换为辐条参数即可。上文提到，长辐条的燃烧过程分为三个阶段，第二、第三阶段燃烧过程与星角第二、三阶段一致，第一阶段与短辐条的第一阶段一致，长辐条燃烧周长与通气面积计算参考上文即可。长辐条研究单元横截面如图9所示，这里不再推导分析。

图9 长辐条横截面示意图Fig.9 General view of long wagon segment

长辐条第一阶段为由侧面向辐条对称轴燃烧的过程，临近这一阶段结束时，辐条尚存在较大的长度和较大的燃面。因此，第一阶段结束时会伴随着燃烧面积的突变，由于突变后与突变前燃面差别较大，且燃面随燃烧肉厚的变化规律不同，可利用长辐条的这一性质使发动机在不同时刻产生两种推力。形成长辐条的参数条件如式(40)所示，反之会形成短辐条：

(40)

1.4.3 圆弧过渡段燃烧周长与通气面积

圆弧过渡段用以连接星角与辐条，是装药燃烧中性质较稳定的部分，燃烧周长随着燃烧肉厚线性增加，圆弧过渡段燃烧周长和通气面积分别为

(41)

(42)

圆弧过渡段在星角第二阶段结束时燃烧殆尽，此时燃烧周长突变为0，通气面积达到最大，即

(43)

2 计算实例与结果分析

依照新型组合树突形装药组合类型1～5设定算例参数，如表3所示，得到五种组合类型研究单元的燃烧周长与通气面积随着燃烧肉厚的变化规律，如图10(a)～(e)所示。

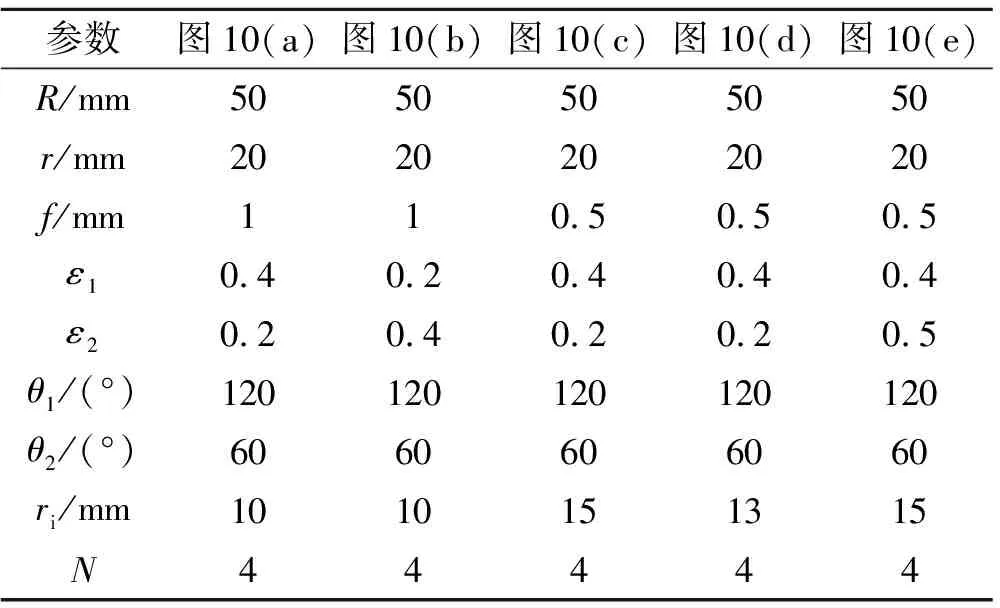
表3 算例参数Table3 Parameters of samples

燃烧面积与燃烧周长变化规律一致，可通过燃烧周长曲线分析燃烧面积的变化特点。对于长辐条与星角组合得到的新型组合树突形装药，由于长辐条本身的燃面突变，会使得新型组合树突形装药也存在燃面突变的情况。适当调整星角参数，可令新型组合树突形装药的燃面大于相同辐条参数下的车轮形装药，长辐条产生的燃面突变导致的燃面变化百分比减小。观察算例曲线，组合类型1新型组合树突形装药中，燃面突变发生于星角燃烧第一阶段之后，使得燃烧初期燃烧面积相对稳定。组合类型2中，燃面突变发生于星角第一阶段燃烧过程中。组合类型2装药不利于燃面的保持，但突变前后燃烧面积都相对稳定，适用于多推力固体火箭发动机。

(a)组合类型1 (b) 组合类型2

短辐条与星角组合得到的三种组合类型的新型组合树突形装药都没有发生燃面突变现象，均适用于燃面连续的情况。组合类型4中由于短辐条结构较接近长辐条，燃烧初期的燃烧面积变化不平滑。组合类型3对应的装药中，星角第一阶段肉厚较小，导致装药只能在较短的阶段内保持相对稳定的燃烧面积。组合类型5可在较长阶段内保持相对稳定的燃烧面积，相比组合类型4曲线，组合类型5燃面曲线在燃烧初期形成的凸起非常小。相比组合类型3曲线，组合类型5燃烧面积相对稳定的阶段更长。对比长辐条与星角组合的两种情况，短辐条与星角组合得到的新型组合树突形装药不会出现燃面突变，因此也就无法运用在多推力发动机上。五种组合类型的装药除燃烧初期燃面变化存在一定差异外，增面过程与余药燃烧过程基本一致。因此，对新型组合树突形装药的选择，主要从燃烧初期的阶段着手。

新型组合树突形装药具有10个可调的结构参数，调整这些结构参数，除能够将该装药改变为星形装药与车轮形装药，得到星形装药与车轮形装药的燃面特性外，还能够得到这两种装药所不具备的燃面特性。更多的可调参数使新型组合树突形装药具备更多可能的燃面特性，适应更多的内弹道需求，应用到更广泛的发动机场合中，如可将该装药运用至点火发动机与有特殊要求的燃气发生器中。

星角与辐条的第一阶段可为增面、减面或等面燃烧。因此，五种组合类型的新型组合树突形装药在燃烧初期均可能为增面、减面或等面燃烧。若星角与辐条的第一阶段及圆弧过渡段燃面变化率之和接近0，就可得到燃烧面积相对稳定的新型组合树突形装药。星形装药与车轮形装药只能在特定的参数组合下，才能使星角或辐条的燃烧面积表现出相对稳定的性质。相比之下，新型组合树突形装药多了上述选择，可通过星角、辐条与圆弧过渡段的增减面性质互补的方式，得到相对稳定的燃面肉厚曲线。

以新型组合树突形装药组合类型5为例，分析燃烧初期燃烧面积相对稳定的原因。星角部分、辐条部分与圆弧过渡段的燃烧周长随燃烧肉厚的曲线如图11所示，下标S表示星角，W表示辐条，T表示圆弧过渡段。星角第一阶段持续到短辐条第三阶段才结束，除上述的三者燃面线性变化阶段增减面性质互补的原因外，组合类型5中短辐条第二阶段燃面曲线形成的弧线部分比较平缓，且这一阶段比较短暂。同时，短辐条第三阶段总体的燃面变化率与自身的第一阶段接近，与星角第一阶段及圆弧过渡段的燃面变化率之和接近0。因此，新型组合树突形装药在整个星角第一阶段中具有相对稳定的燃烧面积。设计中，若使得辐条增面阶段与第一阶段燃面变化率大致相等，星角减面性与辐条和圆弧过渡段增面性互补，同时星角第一阶段肉厚足够大，则新型组合树突形装药可在燃烧初期较长的阶段内保持相对稳定的燃烧面积。

图11 组合类型5辐条、星角与过渡圆弧燃烧周长Fig.11 Burn perimeters of star segment,wagon segment and transition segment of type 5

上文提到的方式虽可得到燃烧面积相对稳定的燃烧过程，但并非严格的等面燃烧。从燃烧周长计算公式可看出，星角与辐条的第一阶段以及圆弧过渡段燃面均为线性变化，等面燃烧可在前两者的第一阶段燃烧都未结束时得到。星形装药要获得等面燃烧的性质，星角数N与星角大小θ2必须要满足一定的对应关系[4]。在θ2与N确定的情况下，如果内径r及星根过渡圆弧半径f都确定，那么第一阶段等面燃烧的燃烧面积只与ε2有关，燃面大小的控制因素较少。

对于本文研究的新型组合树突形装药，参数须满足如下条件，才可得到等面燃烧的装药：

S1S+S1W+S1T=const

(44)

式中S1x为装药相应部分的第一阶段燃烧周长。

可得

(45)

由式(45)可知，当装药星角数N确定后，为得到等面燃烧的第一阶段，依然有无穷多组θ1与θ2的组合。相比星形装药，新型组合树突形装药有更多的参数选择，更容易得到具有等面燃烧性质的装药。等面燃烧面积可通过改变θ1、θ2、ε1、ε2与ri来控制，燃面的控制因素更多。同理，与车轮形装药相比，新型组合树突形装药也具有上述特点。

本文提出的新型组合树突形装药相比星形与车轮形装药，在保证初始燃烧周长及相同结构参数相等的情况下，有更大的装填分数。为证明这一点，需要在上述前提下，得到新型组合树突形装药初始通气面积小于星形或者车轮形装药的初始通气面积的结论即可。假设发动机喉通比始终满足给定条件(即装药喉通比很小，临界喉通比不足以用来约束装药的结构设计)，存在设计好的车轮形装药，保证辐条参数不发生改变，在此基础之上，向装药中加入星角BAC，使装药变为新型组合树突形装药，如图12所示。

图12 车轮形装药变换为新型组合树突形装药Fig.12 Transformation from wagon wheel grain to the new kind of combined dendrite grain

为保证新型组合树突形装药燃烧周长与车轮形装药相等，有

(46)

忽略星根过渡圆弧的影响，由于初始时y=0，可得

(47)

车轮形装药变换为新型组合树突形装药后，由图12可看出，通气面积必然减小，研究包含星角的扇形部分BOC，从公式的角度分析，由式(21)与扇形面积公式得到

(48)

(49)

由燃烧面积相等的关系得到

(50)

其中

(51)

则

(52)

根据式(4)星角不干涉条件，结合式(47)可得式(52)中变量x的取值范围，将式(47)代入式(4)，得

(53)

求导，可得

(54)

观察式(54)等式右边第二项，在(0，π]范围内分母大于0，对分子求导可知，在此取值范围内-xsinx≤0成立，因此分子xcosx-sinx<0成立，所以g′(x)>1成立。可知，g(x)在(0，π]上为增函数，因为g(1)=0，所以x在(0，1]上时，式(53)成立。

x在(0，1]上时，因为1-cos 2x>0成立，故x-sinxcosx>0-sin 0 cos 0=0，推出f′(x)>0在该范围内成立，f(x)>f(0)=0，且f(x)为增函数。因此，将车轮形装药等燃面变化为新型组合树突形装药后，通气面积减少，装填分数相应得到增大。在不超过喉通比限制，且相同结构参数及初始燃烧周长相等的情况下，新型组合树突形装药相比车轮形装药，有更大的装填分数。

与上面的分析同理，在保证星角结构参数与初始燃烧周长不变的情况下，将星形装药变为新型组合树突形装药，可推导通气面积的变化如下，由初始燃烧周长相等得到

(55)

由式(32)可得H的值，通气面积的变化量为

(56)

上式右端第一项大于等于零，因式(2)的限制，第二项必然大于零，所以在保持初始燃烧周长与星角结构参数不变的情况下，星形装药变化为新型组合树突形装药之后，通气面积必然减小，装填分数必然增加。

从横截面分析中可知，在保证星角或辐条结构参数及初始燃烧周长不变的情况下，星形或车轮形装药变换为新型组合树突形装药后，都将使得装填分数变大。因此，新型组合树突形装药有充分利用发动机燃烧室空间的优点。