燃气摆阀作动频率对燃烧室动态影响的数值研究与验证*

2018-07-20杨振华房建卿权维利高天宇安清华王兴起

固体火箭技术 2018年3期

杨振华，房建卿，权维利，高天宇，安清华，王兴起

(中国航天科工集团六院四十一所，呼和浩特 010010)

0 引言

现代导弹对飞行空域及机动性要求越来越高，某些固体火箭发动机安装燃气阀以实现推力大小和方向的控制。燃气阀广泛应用于固体冲压发动机、姿轨控发动机、变推力固体火箭发动机等，因此分析燃气阀作动频率对燃烧室动态影响有着广泛的工程应用需求。燃气阀作动过程中喷管的有效喉面发生改变，进而影响燃烧室压强、燃气流量和推力。为保证发动机具有良好的性能，必须分析燃气阀作动过程中燃烧室压强、燃气流量等参数的改变，为发动机总体设计提供理论依据。

目前，国内在变几何喉道对燃烧室性能影响做了较多的研究。国防科技大学潘余等研究了“变几何喉道对超燃冲压发动机点火与燃烧性能的影响”[1]，西北工业大学冯喜平等做了“基于燃气射流控制的可调进气道数学模型研究”[2]，但没有针对阀门作动频率对燃烧室参数影响方面的研究。某固体姿轨控发动机中使用燃气摆阀作为推力换向的执行机构，燃烧室产生的燃气经过燃气摆阀通往喷管，燃气摆阀通过电磁铁控制进行往复式作动，工作在脉冲状态[3]。

为研究燃气摆阀作动频率对燃烧室动态响应特性的影响，本文利用数值方法，仿真分析了燃气摆阀周期性作动，燃烧室压强、燃气流量响应特征，计算了燃气摆阀以不同频率作动下燃气发生器压强、燃气流量动态响应，并与试验结果进行了对比分析。

1 有效喉面改变规律计算

燃气摆阀见图1，图中箭头表示燃气流动方向，燃气摆阀一个工作周期，摆杆由左侧摆到右侧，再摆回左侧。

图1 摆杆摆动过程示意图Fig.1 Diagram of pendulum swing process

图1中，摆杆位于中间位置时，燃气由两侧同时流出，其有效喉面(AtMID)大于摆杆位于单侧的有效喉面(AtSID)。摆动过程有效喉面会周期性改变。

为得到有效喉面的改变规律，对燃气摆阀作动过程的三维动态流场进行了数值计算，计算得到瞬态流场，见图2。

图2 摆杆摆动过程流场压强云图Fig.2 Pressure contour of pendulum swing process

根据上述计算结果得到的喉面改变规律可近似为图3中的曲线，AtMID=1.5AtSID。图中横坐标以一个作动周期为单位1，纵坐标以AtSID为单位1。

图3中，横线部分为摆杆停靠在单侧喷管的有效喉面，曲线部分为摆杆摆动过程的有效喉面。从已有试验数据判读，对于固定的燃气摆阀，在不同作动频率下，其摆杆摆动时间为一固定值。所以，燃气摆阀作动频率越高，周期越短，单个周期内曲线部分占比越高，平均有效喉面越大。

图3 有效喉面改变规律Fig.3 Law of effective throat area

2 作动频率对动态响应影响的计算方法

2.1 模型简化

为简化计算，做如下假设：

(1) 燃气摆阀作动过程中，燃面位置固定，燃气发生器自由容积保持不变；

(2) 假设气体为单相理想气体，不考虑多相流，不考虑化学反应导致的气体参数改变；

(3) 忽略重力对气流的影响；

(4) 燃气入口质量流率模拟固体推进剂燃速方程，满足：

式中Ab为燃面面积；ρ为推进剂密度；a为燃速系数；p为燃烧室压强，n为压强指数。

在上述假设条件下，依据有效喉面面积以及发动机实际燃气流量，将三维发动机模型简化为二维轴对称模型，减少计算的工作量。

2.2 计算方法

本文采用Fluent14.0软件,使用动网格技术和用户自定义函数(UDF)，用数值方法模拟燃气摆阀作动过程中有效喉面改变过程。采用基于压力求解N-S方程，湍流模型使用SSTk-ω模型，动网格使用动态铺层(Layering)方法。

依据图3中有效喉面改变规律，得到有效喉道边界的运动速度，通过UDF控制喉道边界径向速度来实现对喉面的控制，采用动态铺层(Layering)方法建立动网格，网格运动过程见图4。

3 动态响应计算及结果分析

3.1 瞬态计算

在加载动网格前将燃烧室流场计算收敛，在稳态计算的基础上，加载动网格，使用有效喉道边界的周期运动，模拟燃气阀的周期作动。

3.1.1 作动频率为33 Hz动态响应

33 Hz频率对应周期为30 ms，计算得到燃烧室压强响应曲线和燃气质量流率响应曲线，见图5、图6。文中压强(流量)均采用摆杆稳定于单侧对应的压强(流量)值为1作无量纲化处理。

图4 Layering动网格Fig.4 Layering dynamic mesh

图5 33 Hz燃烧室压强动态响应曲线Fig.5 Dynamic response of chamber pressure at 33 Hz

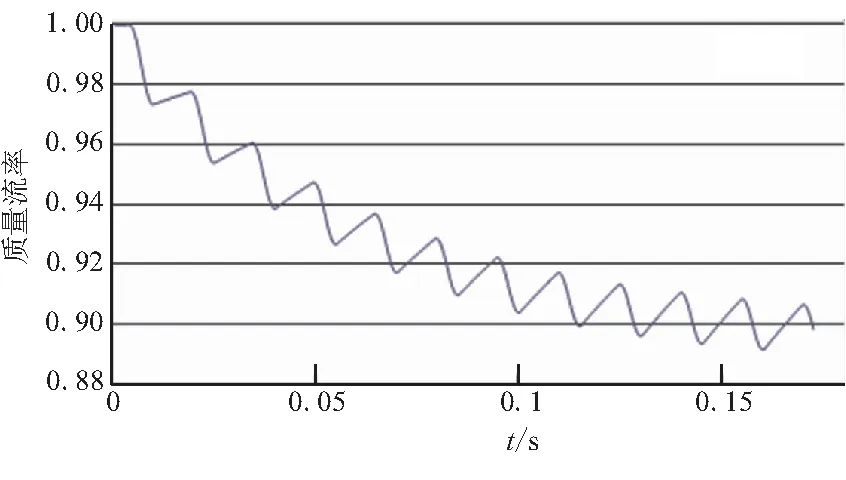
图6 33 Hz燃气质量流率动态响应曲线Fig.6 Dynamic response of mass flow rate at 33 Hz

由图5可见，稳态时，即对应摆杆位于单侧时，压强为1，开始作动之后，燃烧室压强呈周期性上升/下降，并逐渐趋于一个稳定值附近波动，图5中质量流率也有相同的趋势。

3.1.2 作动频率为25、20 Hz的动态响应

25、20 Hz计算得到燃烧室压强的动态响应曲线见图7。

由图7可见，25 Hz和20 Hz时，压强曲线的趋势与33 Hz类似，不同的是压强波动的幅度和趋于稳定后的均值有所不同。

根据计算结果，可以将燃气摆阀周期性作动对燃烧室参数(压强、燃气质量流率)的影响分解为两个方面进行分析：

(1)燃烧室参数在燃气摆阀作动一个周期内，基于该周期内的平均值上下波动；

(2)燃烧室参数的周期平均值随时间下降，趋于一个固定的值。为更直观地分析参数动态响应趋势，引入燃烧室稳态参数的定义：燃烧室周期平均值趋于稳定后的值。

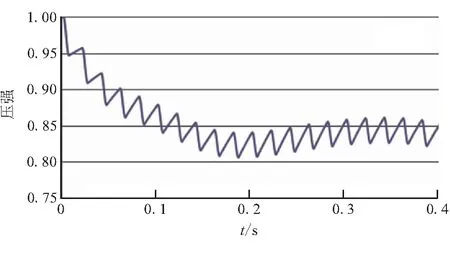
(a)25 Hz

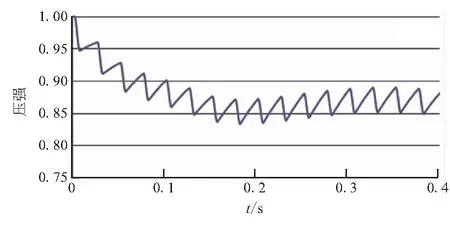
(b)20 Hz

3.2 计算结果分析

3.2.1 燃烧室稳态参数分析

在燃气摆阀开始作动后，燃烧室稳态参数持续下降，到某数值后趋于稳定。可引入一条趋势线来模拟平均值的改变，以25 Hz作动频率下燃烧室压强动态响应为例，用三阶多项式拟合，可表征该燃烧室稳态响应参数，其趋势线见图8。

图8 25 Hz燃烧室稳态压强响应趋势线Fig.8 Steady trend of chamber pressure response at 25 Hz

从3.1节中的计算结果可得：

(1)燃烧室在燃气摆阀周期性作动影响下，燃烧室压强动态响应特征与燃气质量流率动态响应特征基本一致。

(2)在不同燃气摆阀作动频率作用下，燃烧室动态响应频率虽然不同，但其趋势都是先逐渐下降，然后趋于一个稳定的值。

(3)燃烧室稳态参数下降值与作动频率有关，频率越高，下降值越大。

用单位1表示摆杆位于单侧喷管时的燃烧室压强和燃气质量流率，表1中列举了不同作动频率下，燃烧室稳态压强、燃气稳态质量流率趋于稳定后的相对值。

表1 燃烧室稳态参数在不同作动频率下的相对值Table1 Relative values of steady chamber parameters at variable frequencies

由表1可得出，燃气摆阀作动频率越高燃烧室稳态参数改变越大，进而得出燃气摆阀作动频率越高对发动机性能影响越大。燃烧室参数稳态参数随频率改变曲线见图9，纵坐标值为燃烧室参数较燃气摆阀作动前下降百分比。

图9 燃烧室稳态参数随频率改变Fig.9 Steady trend of chamber pressure response

由图9可得，当该燃气摆阀以20～33 Hz范围内作动，燃烧室稳态压强相比燃气摆阀位于单侧稳态压强下降的比值为14.9%～20.5%，燃气稳态质量流率降低比值为7.9%～11.2%，频率越高，下降幅度越大。

3.2.2 燃烧室参数基于稳态参数的波动

在燃气摆阀周期性作动下，燃烧室参数基于稳态值上下波动，其波动频率与燃气摆阀动作频率一致。每个作动周期内，燃烧室参数波动值与作动频率有关。分别采集燃气摆阀以33、25、20 Hz作动下情况下，燃烧室平均参数趋于稳定后的燃烧室压强波动值与燃气摆阀作动前燃烧室压强比值、燃气质量流率波动与燃气摆阀作动前燃气质量流率比值进行分析，波动比值见表2。

由表2可知，作动频率越高，燃烧室参数波动幅度越小，这是因为燃烧室压强响应较慢，作动频率越高，周期越短，压强波动幅度越小。对比表1、表2可见，燃烧室参数稳态值较燃气摆阀作动前下降的幅度大于一个周期内的波动幅度值，因此要着重分析稳态值下降的规律。

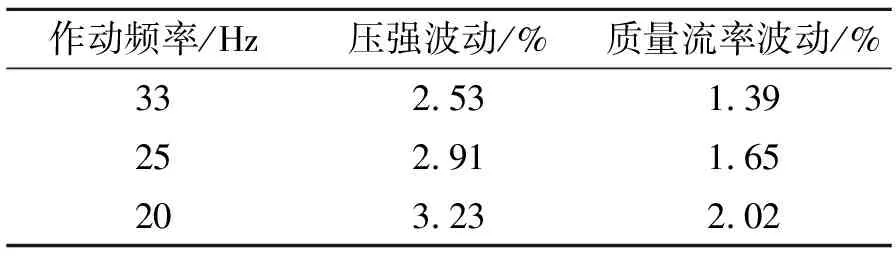
表2 燃烧室参数在不同作动频率下的波动Table2 Fluctuation of chamber parameters at variable frequencies

3.2.3 压强稳态值下降规律分析

经分析，燃烧室稳态压强在燃气摆阀开始作动后下降，是由于燃气摆阀作动过程增大了一个周期内的平均有效喉面。在一个周期内，时间加权平均喉面公式见式(1)。

(1)

因摆杆摆动时间为固定值，所以周期越短，摆动时间相对于周期越长，即图3中正弦曲线部分占一周期的比例越大，周期平均喉面越大。燃速定义的质量流率公式为

(2)

气体动力学流量公式为：

(3)

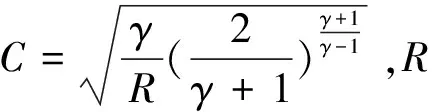
当流量达到稳定，即燃面质量流率等于喉道处质量流率的情况下，假定燃气组分、Ab、T0不变，联立式(2)和式(3)，可得到平衡压强公式：

(4)

式(4)中，constant为常数，燃烧室压强与有效喉面的(1/n-1)次幂成正比，本文中推进剂n=0.5。根据图3中的有效喉面改变规律，计算得到的周期平均喉面代入式(4)，可得到燃烧室压强下降比值，其数值见表3。

表3 不同频率的有效喉面与压强改变比值表Table3 Effective throat area and pressure changes at variable frequencies

从表3可看出，对比CFD仿真结果与式(4)理论计算结果，CFD仿真结果与理论值能较好的吻合，CFD仿真值与理论值的误差，比数值计算的一个周期内压强波动的幅值小。表明可用周期平均喉面来计算燃烧室稳态压强。

4 仿真与试验对比分析

进行了安装两个相同燃气摆阀的发动机热试车，燃气摆阀AtMID=1.5AtSID，作动周期为10 Hz，摆杆摆动时间为3 ms，试验得到了燃烧室压强曲线。将数值仿真得到的稳定值与燃烧室平衡压强比较，如图10所示。

图10 试验与计算压强对比(10 Hz)Fig.10 Comparison of pressure between experiment and calculation at 10 Hz

图10中，pEXP为试验压强曲线，在点火阶段边上升边波动；pAtSID为根据AtSID预示的平衡压强；pSIM为仿真得到趋于稳定后的压强波动曲线；pBLC为式(5)预示的平衡压强。

从图10可见，在燃气摆阀作动时，燃烧室压强会以相同的频率波动，由于使用了两个燃气摆阀，在0～0.9 s之间两个燃气摆阀同时切换，但相位不一致，因此波动曲线出现“大小齿”间隔的锯齿形；0.9～1.1 s之间，一个阀门摆杆在单侧，一个阀门切换，压强波动幅度变小；1.1～1.4 s之间，压强达到平衡，两阀门同相位切换，出现了规律的锯齿形，且周期稳态压强、压强波动幅度均与仿真结果吻合较好。试验和仿真曲线一致表明，阀门作动、有效喉面增大时，燃烧室压强下降响应时间小于0.5 ms，而喉面恢复初值后，压强上升的响应时间在50 ms以上。

周期平均值分析：

根据式(1)得，周期平均喉面：

根据式(4)得，平衡压强：

图10中，试验曲线平衡段压强范围：pEXP=0.970 5±0.008 1，压强波动幅度0.008 1；对应的仿真曲线压强范围pSIM=0.955 7±0.008 6 压强波动幅度0.008 6。

该燃气摆阀10 Hz作动的压强波动幅度低于表1中20～33 Hz的幅度，是因为该燃气摆阀摆杆摆动时间短，周期平均喉面小，引起燃烧室压强波动小。

根据平均喉面预示的平衡压强与试验值误差0.8%以内；仿真结果预示稳态压强与试验相对误差为1.6%以内，仿真预示压力波动幅度相对误差6.2%以内。表明使用周期平均喉面可以精确的预示平衡压强，使用数值仿真可较精确地预示压强波动幅度。