基于非线性互依赖性的癫痫致痫区识别方法研究

马 震

(滨州学院信息工程学院,山东 滨州 256600)

引言

癫痫是仅次于中风的第二大神经疾病，因为其发作频繁、患病人群广而一直被广泛关注[1-2]。癫痫发作来自于异常兴奋的局部脑区域，称为致痫区(epileptogenic zone, EZ)[3-4]，也就是癫痫的病灶。致痫区大量神经元出现过度兴奋并迅速波及相邻神经元，导致神经元超同步化放电，从而引发癫痫发作。所以，无论采取手术、药物以及电刺激的方法[4]治疗癫痫，致痫区的准确识别是首要的任务，是保证治疗效果并降低副作用的关键。当癫痫行为同时涉及几个电极的时候或者当癫痫发作的形态比较模糊的时候，传统的视觉诊断很难定位发作的源头。因此，需要应用信号处理的方法挖掘EEG信号中更多的信息来辅助视觉诊断[5]。

癫痫发作期间，神经群超同步放电的原因是神经群之间的异常耦合。研究表明这种异常耦合是非线性的[6]，所以非线性动力系统的理论往往被用来分析引发癫痫的神经元网络动力学的变化[7-8]。可以把致痫区和非致痫区分别看作单独的动力系统，致痫区是驱动方，其他区域为响应方。所以，致痫区识别可以看作一个驱动方识别的问题。而如何根据EEG信号波形确定不同脑区域之间耦合的方向和强度信息，是致痫区识别问题的关键。本研究提出了一种灵敏度可调节的非线性互依赖性测度，并用以进行致痫区识别。

因为影响癫痫发作的因素很多且范围较广，所以用临床实验的方法来定量研究它们的影响很困难。为了验证本研究方法在致痫区识别方面的效果，笔者采用了Jansen等[9-10]提出的神经群模型(neural mass model,NMM)来对该方法进行了仿真。虽然改进的Jansen模型或者可以产生更加丰富的波形[11-12]，或者具有更简单的表示方式[13]，但是这些模型中的某些参数并不具有明确的生理学意义，所以采用了模型参数具有生理学意义的Jansen模型。

1 神经群模型

1.1 本地神经群模型结构

本地神经群的结构如图1所示。在Jansen模型中，神经群由锥体神经元子群(见图1(a)阴影部分)和中间神经元子群(见图1(a)无阴影部分)，椎体神经元接受中间神经元兴奋和抑制的反馈，而中间神经元只接受椎体神经元兴奋的反馈，反馈的强度以及延迟时间都可以通过模型参数来调节。每个子群都由两个部分组成，分别是将行动电位发放率转换为后突触电位(postsynaptic potential， PSP)的线性模块和将后突触电位转换为行动电位发放率的非线性模块组成。

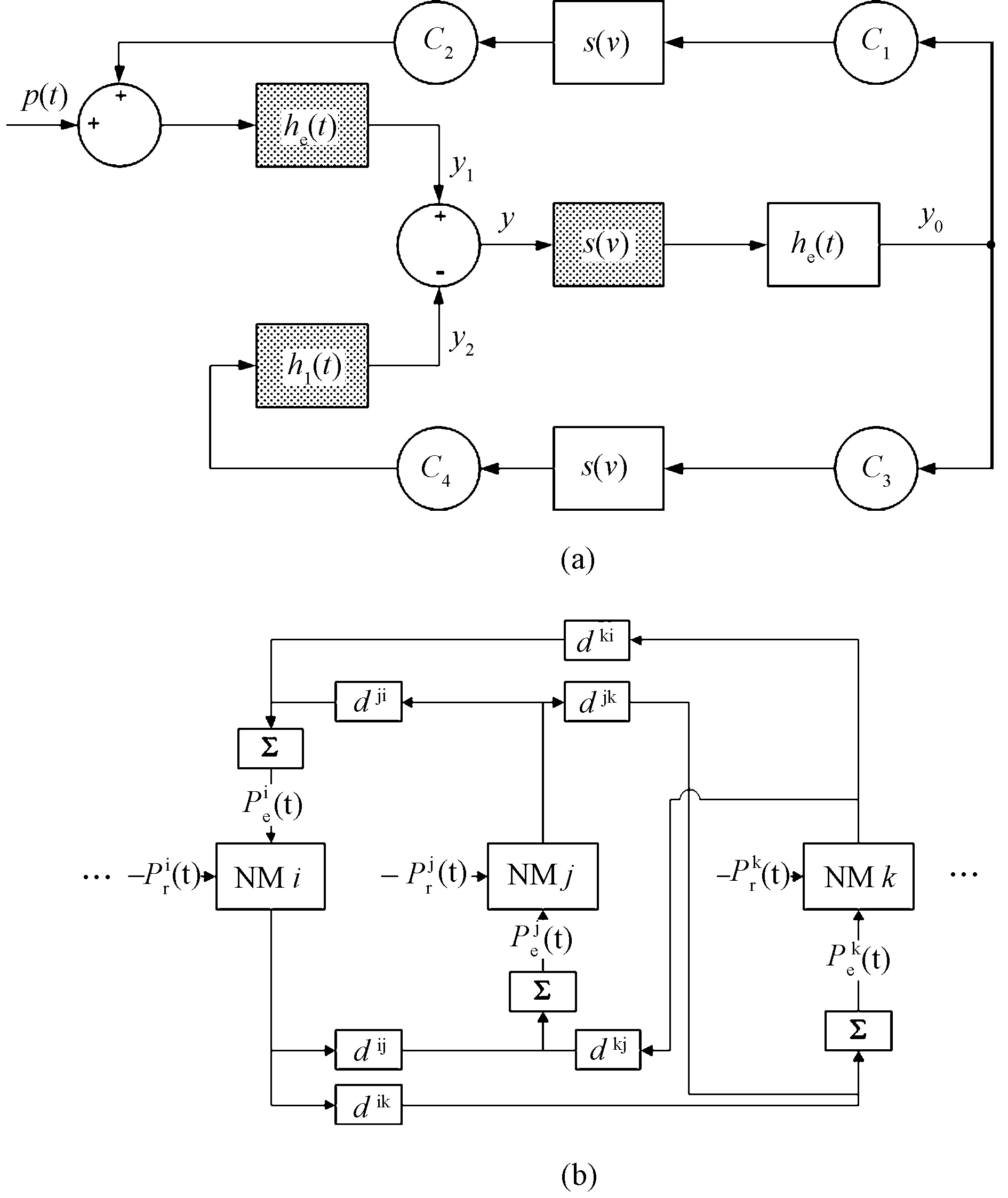
图1 神经群模型结构。(a) 单神经群模型结构；(b) 耦合的神经群模型结构Fig.1 Neural Mass Model. (a) Local architecture of a neural mass model; (b) Structure of multiple neuronal populations model

线性模块的单位脉冲响应为

(1)

可以将兴奋/抑制神经子群的平均行动电位发放率m(t)转换为平均后突触电位v(t)，也就是v(t)=he,i(t)*m(t),这里*为卷积运算符。式(1)中下标e和i分别表示兴奋和抑制神经子群。参数Ae,i可以分别用来调节兴奋和抑制突触的强度，τe,i为时间常数，代表了突触上的延迟。在本研究中，通过调节Ae来改变神经群模型的兴奋程度，形成兴奋程度较高的致痫区神经群模型来产生癫痫样的信号。

非线性模块可以用一个静态函数S(v)来表示，椎体神经元和中间神经元之间兴奋/抑制突触的数目是由C1～C4共4个连接常数来描述，可以参考之前的工作来了解它们的详细信息[9-10,14]。

1.2 耦合的神经群模型

癫痫行为的产生和传播与属于不同大脑区域的多个神经群有关，可以用耦合的神经群模型来表示。锥体神经元是通过轴突与脑部其他区域的兴奋神经元进行联系，本研究通过将一个群中锥体神经元的输出作为其他神经群的兴奋输入，实现不同大脑区域神经群之间的耦合，其结构如图1(b)所示。

从图中可以看出，每个本地神经群都接受来自于外部的输入P(t)，包括来自于与本群耦合的神经群和与本群无耦合的神经群的输入。本研究中，Pr(t)表示与本群无耦合的远方神经群对本群的影响，它可以采用高斯噪声来表示。Pe(t)为与本群耦合的神经群对本群的输入，它具有如下形式,即

(2)

式中：Pei(t)表示神经群模型i的耦合输入，也就是与神经群i有直接耦合关系的其他神经群对本群的影响；N为涉及的神经群数；dji(t)为神经群之间传播通道的单位脉冲响应，具体表示为

(3)

式中：Kji为神经群j和神经群i之间的连接常数，代表了不同时刻神经群之间的耦合强度，不同群输出信号之间的同步性会随连接常数的增加而增加，这也是导致癫痫发作的主要原因；τd为群间的传播延迟；yj(t)为神经群j的输出。

2 致痫区识别

神经群的同步是区分正常和非正常脑功能的重要特征[15-16]，癫痫发作时大量的神经群超同步放电并进行传播的过程可以看作两个耦合的动力系统之间耦合强度增加的过程[17-18]。致痫区可以看作驱动方，而非致痫区看作响应方，所以致痫区识别可以看作驱动方识别的问题。驱动方识别不仅需要动力系统之间耦合的强度信息，还需要它们之间耦合的方向信息。

相空间中驱动方的轨迹决定响应方的轨迹，反之则不成立。非线性互依赖性的基本思想是通过度量不同系统之间的相似性来确定驱动方/响应方。本研究提出了以相空间中各点距离的加权排位作为描述相空间差异的指标，来检测从EEG中获得的耦合方向信息，从而确定致痫区位置。

2.1 非线性互依赖性

对于来自于两个动力系统X和Y的两个时间序列xn和yn(其中n=1,…,N)，重构相空间得到xn=(xn,…,xn-(m-1)τ)和yn=(yn,…,yn-(m-1)τ)，这里m为嵌入维数，τ表示时间延迟，从而得到X=(x1,…,xN)和Y=(y1,…,yN)。

进而，对于同一动力系统不同时刻状态之间的自相异性进行度量，有

dij(X)=d(X)(xi,xj)=d(X)(xj,xi)

(i=1,…,N；j=1,…,N)

(4)

自相异性具有对称性，也就是dij(X)=dji(X)。令Dij(X)表示包括所有N×N个dij(X)的相异性矩阵，dij(Y)和Dij(Y)与dij(X)和Dij(X)的定义方法相似。

非线性互依赖性是采用加权排位的比值来表示某个dij(Y)的小值(大值)对应着dij(X)也是小值(大值)的几率，来描述不同动力系统之间的相似性。对于每个固定的i和j，用gij(X)来表示dij(X)在升序排列的自相异性集合{dil(X)}，l=1,…,N中的排位。

令rn,j和sn,j，j=1,…,k，分别表示xn和yn的k个最近邻矢量的时间索引。k个近邻的加权平均排位定义为

(5)

而k近邻的条件平均排位定义为

(6)

在本研究中，定义一种非线性互依赖性测度为

(7)

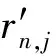
(8)

而k远邻的条件平均排位定义为

(9)

则可以定义另一种非线性互依赖性测度为

(10)

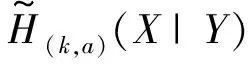
(11)

这里，a为小于1的系数。

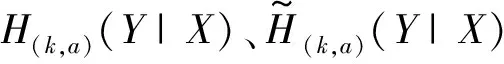
2.2 癫痫致痫区识别

基于非线性互依赖性指标的癫痫致痫区识别步骤如下：

1)根据来自于两个神经群X和Y的脑电信号x和y确定群间延迟。a可以用来调节L(k,a)对定向耦合强度的敏感程度，k值的大小决定了L(k,a)对信号相空间描述的完整程度，根据信号的特性选取合适的k和a，分别计算不同数字时间延迟nd下的xn和yn-nd的L(k,a,nd)(X|Y)和L(k,a,nd)(Y|X)。这里nd代表x和y之间的相对延迟，可以为正整数、负整数或0。

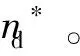
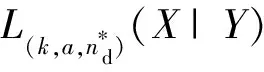
3 结果

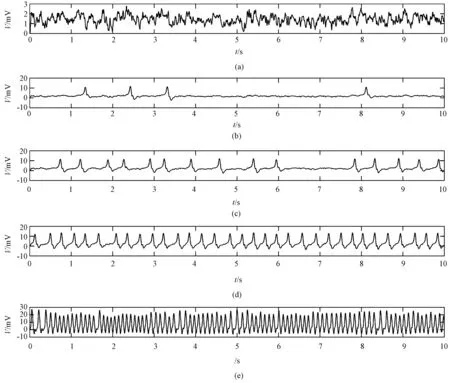
图2 不同A值时模型的输出。(a)A=3.2; (b)A=3.5; (c)A=3.6; (d)A=3.9; (e)A=8.4Fig.2 Model outputs with different values of A. (a)A=3.2; (b)A=3.5; (c)A=3.6; (d)A=3.9; (e)A=8.4

3.1 不同兴奋性的神经群模型输出

癫痫发作不同时期，神经群的兴奋性、抑制性都不相同，从而产生不同的脑电信号。保持抑制性强度不变(Ai=22),兴奋性强度逐渐增加，模型的输出信号如图2所示。

图2(a)给出了Ae=3.2的模型输出波形，反映了正常的脑电信号波形。随着A逐渐增加，模型输出波形如图2(b)～(e)所示。兴奋程度的增加导致零星的尖波出现(从Ae=3.5)，然后频繁地(Ae=3.6)出现，最后有节奏地(Ae=3.9)出现。尖波发放的平均频率随着Ae的增加而增加。当Ae=8.4，模型输出从尖波转到棘波。从图2可以看出，不同Ae值模型所产生的波形与颞叶癫痫发作过程中的波形变化相似，所以模型可以有效地模拟真实的神经生理过程及脑电活动。

3.2 非线性互依赖性随单向耦合强度增加的变化

建立了两个单向耦合的Jansen神经群构成的模型，分别代表致痫区与非致痫区。为了讨论不同参数对L(k,a)性能的影响，这里群间相对延迟为0，也就是不考虑群间的延迟。

对于所建立的模型，神经群1～神经群2的单向耦合强度值K12从0逐步增加到400，步长为2，a分别采用0.9和0.5，k分别采用50和10来计算L(k,a)(X|Y)和L(k,a)(Y|X)，结果如图3所示。可以看出，随着耦合强度值的增加，用不同(k,a)组合计算出的L(k,a)(X|Y)和L(k,a)(Y|X)总体上都是增加趋势并达到某个稳定值。

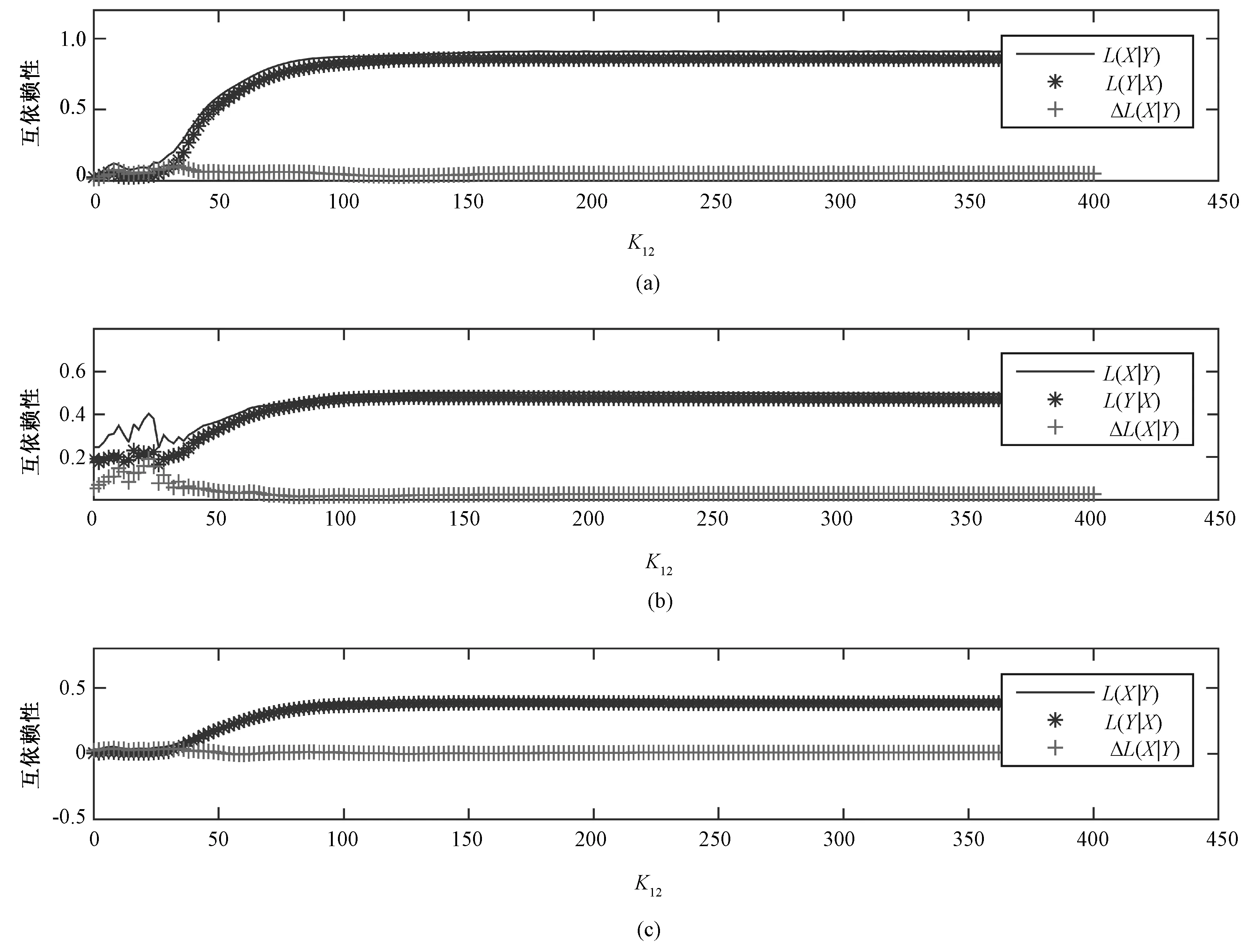
图3 不同a、k值的L和ΔL随K12的变化。(a)a=50,k=0.9；(b)a=50,k=0.5；(c)a=10,k=0.9Fig.3 L(X|Y)(solid lines), L(Y|X)(stars) and ΔL(X|Y)(crosses) with different values of a and k as a function of coupling strength K12. (a)a=50,k=0.9; (b)a=50,k=0.5; (c)a=10,k=0.9

3.3 致痫区识别结果

3.3.1群间无延迟的致痫区识别结果

依然采用上述模型，两个神经群之间单向耦合强度逐渐从0增加到200，然后再递减为0，步长为1，群间延迟保持为0。为了验证本研究致痫区识别方法对于不同致痫区的适用性，神经群1(致痫区神经群)模型的兴奋突触强度Ae1从1增加到8，步长为0.5，而神经群2的模型参数保持标准值3.25。对于不同的致痫区，都采用k=50，a=0.9进行非线性互依赖性计算，识别结果如表1所示。

当神经群1的兴奋突触强度为1.0、5.5、6.0的时候，采用本研究方法可以100%正确识别致痫区神经群。除去兴奋突触强度为7的情况，本研究方法都可以达到95%以上的正确率。总的识别正确率为98.24%。

3.3.2群间有延迟的致痫区识别结果

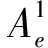
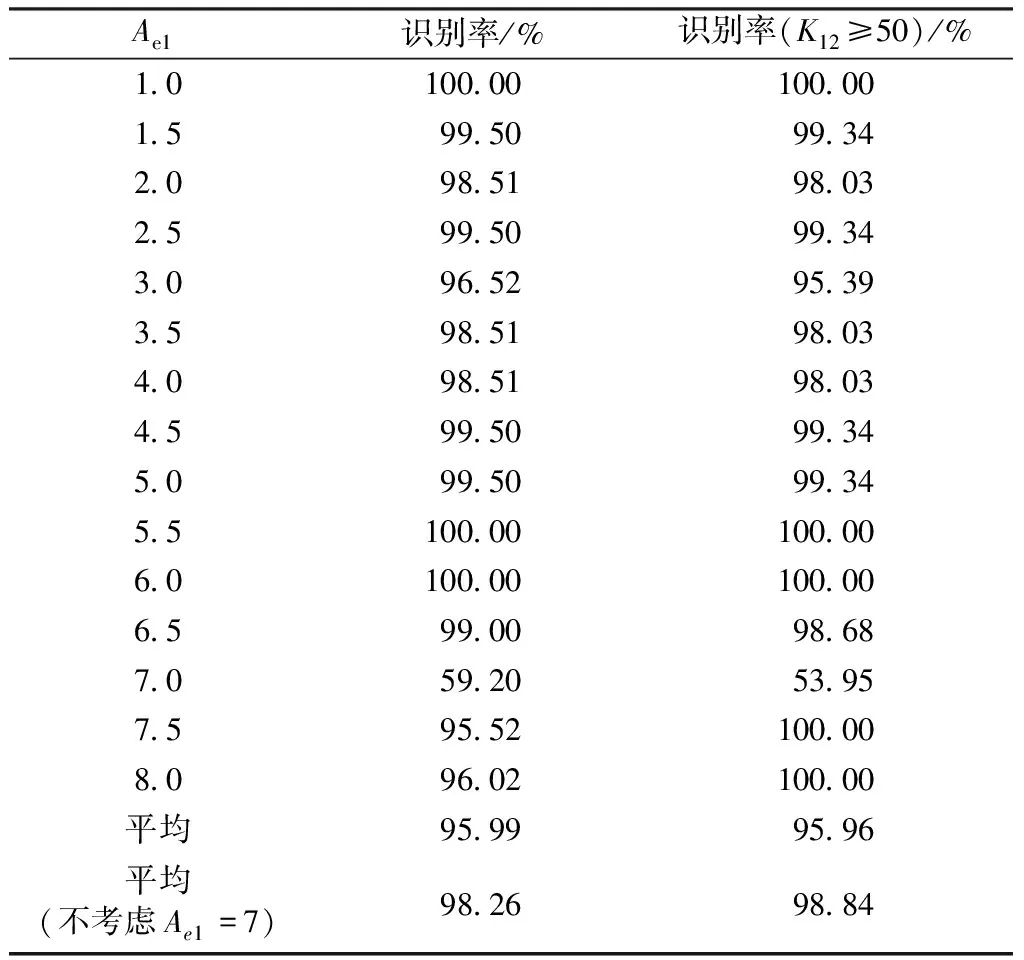
表1 无延迟时不同致痫区的识别率

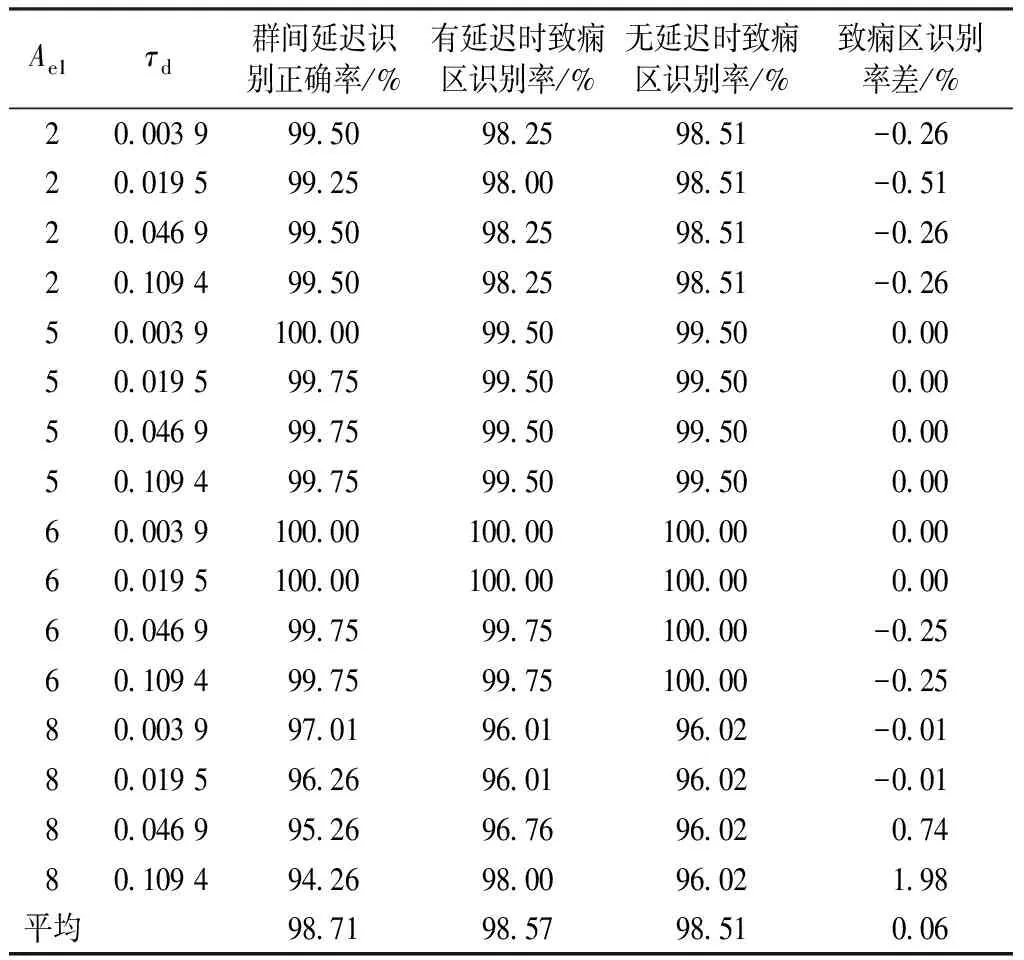
表2 有延迟时不同致痫区的识别率

从表中可以看到，当神经群1的兴奋突触强度为5、6的时候，群间延迟识别正确率都可以达到100%，平均值分别为99.81%和99.88%；兴奋突触强度为2时，群间延迟识别正确率的均值也可以达到99.44%；兴奋突触强度为8时，群间延迟识别正确率的均值只有95.7%，这主要是因为兴奋突触强度为8时，模型的输出信号周期性已经比较强，会干扰本研究方法的识别结果。

4 讨论

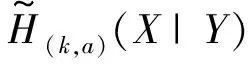
实验结果( 见图3)表明，当K12小于20的时候，L(k,a)(X|Y)和L(k,a)(Y|X)都有所波动，这说明在耦合强度较小的时候，X和Y之间的同步并不明显，存在一些因偶然因素导致非线性互依赖性值的变化。当K12到达某个较大值的时候，L(k,a)(X|Y)和L(k,a)(Y|X)也达到某个较为稳定的值，这说明当耦合强度增加到一定程度，继续增加耦合强度并不能继续改变驱动方和响应方相空间结构之间的差异，所以互依赖性值也就不再随之变化。但是，由于a不同，这个稳定值的大小不同，这也说明了a对相空间差异的放大作用。可见，a可以用来调节L(k,a)对定向耦合强度的敏感程度，a越小则L(k,a)对相空间差异越敏感，也就是会在较大程度上放大驱动方和响应方相空间结构之间的差异，反之，a越大，则这种放大的程度就会越小。所以，对于相空间差异较小的信号，需要选择较小的a。k描述了对X和Y相空间中进行比较的点的个数，k值的大小决定了L(k,a)对信号相空间描述的完整程度。当k=10时，只考虑相空间中10个点的差异，会出现一些意外情况，导致L(k,a)并不能随耦合强度的增加而增加，会出现波动。而随着k的增加，这种波动会逐渐减小，L(k,a)会随着K12的增加较为稳定地增加，直到耦合强度的增加不能改变X和Y相空间相似程度，L(k,a)会趋于稳定值。

在癫痫发作期间，致痫区神经群与其他神经群之间的耦合强度较大。对于群间无延迟的情况，如果单纯考虑耦合强度超过50的情况，有1.0、5.5、6.0、7.5、8.0的情况都可以达到识别率100%，而除了7的情况，其他都可以达到95%以上，总识别率为98.84%。当Ae1=7的时候，识别率只有59.20%。这是因为随着耦合强度的增加，神经群1和神经群2两个动力系统的相空间快速变得相似，k=50的情况下，不能很好地区分驱动方和响应方，存在偶然性导致L(k,a)(X|Y)

在正确识别群间延迟的基础上，致痫区的识别就等同于无延迟的情况，所以对各类病灶均取得了较好的识别率，平均识别率可以达到98.57%。在兴奋突触强度为8的情况下，受输出信号周期性较强的影响，延迟识别正确率并不高，但其致痫区平均识别率却可以达到96.7%，高于无延迟的识别率96.02%。这是因为周期性较强的信号，其延迟一个或多个周期并不会对其相空间轨迹有较大的影响，所以在群间延迟为0.046 9 s和0.109 4 s的时候取得了比无延迟情况下更高的识别率。总体而言，有延迟时的致痫区识别率与无延迟时的相差不大，平均提高0.06%，这主要是因为兴奋突触强度为8、群间延迟为0.109 4 s时，致痫区识别率得到了较大的提升；排除这种情况，致痫区平均识别率略下降0.07%，与无延迟的情况基本持平。当前，癫痫自动控制主要是通过反馈电刺激等打破不同脑皮层区域之间同步性，而并不进行致痫区识别，本研究方法为针对致痫区的自动控制方法提供了理论基础[19-20]。

当前，癫痫致痫区识别多依赖于人工视觉诊断。通过观察多导联的脑电数据，根据波形的特征来确定致痫区。棘尖波是致痫区最常用的标识，高频振荡波也可以有效地揭示致痫区的位置[21]。MRI、PET 及SPECT等可以提供更多的致痫区特征，也被应用于致痫区的识别中[22]。传统的方法多根据不同设备提供的信号来提取致痫区信号的特征，从而确定致痫区。而本研究方法不根据脑电信号波形，而是根据不同区域脑电信号波形之间的耦合关系来确定驱动方，从而确定致痫区。可以作为传统方法的补充，更准确地进行致痫区定位。

5 结论

癫痫致痫区识别问题可以看作一个驱动方识别问题，本研究提出了一种非线性互依赖性指标来作为驱动方的标识。在搭建的神经群模型平台上，对基于非线性互依赖性的致痫区识别方法进行了仿真。实验结果显示：在无群间延迟的情况下，可以取得较高的致痫区识别率；而对于有群间延迟的情况，也可以在较好地确定群间延迟的前提下，取得与无延迟情况下接近的识别率。对于周期性较强的致痫区输出，虽然在群间延迟的识别正确率不是非常高，但是这并不妨碍可以取得接近于甚至高于无延迟情况的致痫区识别率。这说明，该方法对不同的致痫区类型及群间延迟情况有较好的适应性和鲁棒性。如何根据实测的脑电信号来进行致痫区识别，是该方法应用于临床的关键，也是下一步需要研究的问题。