振弦式仪器振动过程探析

齐冀龙，任建钦，刘 枫

（1.中水东北勘测设计研究有限责任公司，吉林长春 130061；2.水利部寒区工程技术研究中心，吉林长春 130061）

1 振弦式仪器

振弦式仪器发明于20世纪30年代，后来经过不断改进逐渐完善以其坚固耐用，便于远距离传输等优点在工程安全监测中获得了广泛的应用[1]。

1.1 仪器内部构成

振弦式仪器内部包括中间张紧的钢弦、永久磁铁、感压膜片、激励与接收线圈。振弦式仪器受到外部的应力时，导致钢弦内的张力T发生变化，从而导致钢弦的共振频率 f发生变化，通过激励及拾振线圈，首先通过扫频激励钢弦，即通过频率不断变化的电流进入激励线圈产生交变的磁场，磁场作用于钢弦，使钢弦处于受迫振动状态，当扫频激励信号的频率接近于钢弦的共振频率时，钢弦便处于共振状态，这时去掉扫频激励信号，钢弦由于处于共振状态，会以共振频率继续振动一段时间，这时振动的钢弦切割磁力线从而在拾振线圈中产生感应电动势，通过拾振线圈采集到此时的共振频率，通过共振频率与外部应力之间的关系可推算出应力的大小，也就可以得知埋设该传感器的位置的受力情况等物理量。

1.2 仪器简化

若要得到振弦式仪器的共振频率与钢弦张力间的对应关系，可以采用如下的方式。

不考虑重力的作用，可以列出如下的力的关系[2]：

图1 钢弦（x，x+dx）间的受力情况

水平方向：

垂直方向：

由于钢弦振动幅度很小，α2和α1很小，钢弦是微振动，弦的伸长以及弦的线密度的变化均可忽略不计，所以这段弦的质量为x，质量乘以垂直方向的加速度应该等于F2，可得：

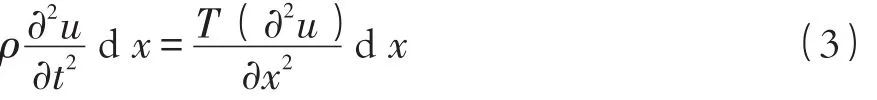
对于一般情况，可以假设钢弦是均匀的可以得到如下的方程式[2]：

由于弦在两个端点处的位移为0，可以得到如下的方程式[2]：

式（5）中 a2=T/ρ；

φ（x）为t=0时的弦上各点的位移与x间的函数；

ψ（x）为t=0时的弦上各点的速度与x间的函数关系。

上述方程（5）—（7）即为钢弦在忽略重力下的波动方程。

上述方程可以采用分离变量法求解。

2 激振过程的数学模拟

2.1 数学模型建立

为模拟振弦各频率的激励过程，简化为如下过程，假设电磁铁对钢弦的力的作用点在钢弦l/2处，作用一大小为ρ的力：

其中 ρδ(x -l/2)为激励线圈对单位质量的钢弦产生的作用力的幅度，sinωt表示作用力是受迫振动，在这种情况下，钢弦的受力可以如下方程表示：

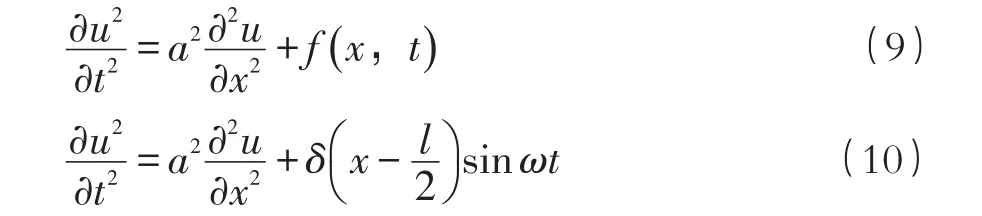
式（10）中0＜ x＜l

边界条件为：

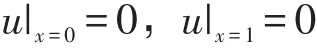
不妨设初始条件如下：

为简化起见，设a=1，l=1，

求解上面的方程，可得到位移的解为：

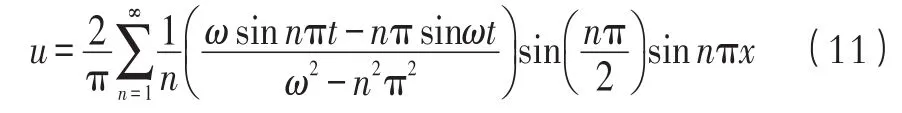
上式中的n代表了不同频次的谐波，由于采集钢弦振动信号时，往往只采集基频振动，将上式的n取为1，可以简化为

2.2 模拟结果分析

选取x=0.5位置的点，由式（12）可知共振频率为ω=PI。分别选取ω=0.1PI、0.5PI、0.75PI、0.98PI、1.05PI、1.50PI，其振幅变化过程见图2。

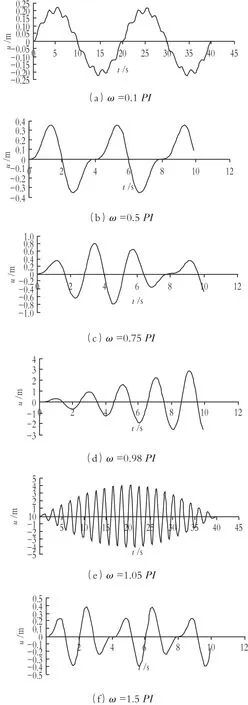
图2 不同共振频率的幅度变化曲线

通过选取不同的激励频率，可以看出在远离共振频率的区域，钢弦处于周期振动状态，其幅度很小；随着激励频率接近于共振频率，其幅度逐渐加大。但是什么时间振幅会达到最大值或比较大的值，保证去掉激励信号后，仍能保持足够的振动时间以便于测量，则需要进行估算并结合试验进行确定。

实际的扫频过程类似于上述信号随着时间依次叠加，由于阻尼或损耗使较小的幅值的信号很快衰减，只留下较大的共振信号。

3 结语

由于振弦式仪器在安全监测工程内观测量应用较为广泛，所以对钢弦在激励信号下的振动过程的深入探讨有助于振弦式监测仪器的开发，本文对模拟过程进行了简化，实际还可以增加对阻尼等衰减作用的考虑得到更为详细的模型。由分析可知，频率激励信号的持续时间及采集信号的时间选取是振弦式仪器采集设备的开发的重要部分。