几种常用求导方法在高等数学中的应用
2018-07-17赵晓艳
◎赵晓艳
(河南质量工程职业学院基础教学部,河南 平顶山 467000)
一、导数的起源
导数的概念最先由牛顿(牛顿称之为流数)和莱布尼茨创立,但其概念模糊.柯西(1821)对导数的概念做出了清晰的定义[1],即导数为差商的极限.德国的魏尔斯特拉斯使极限的概念进一步严格化(即e-N说法),这使导数的定义更清晰.导数亦名纪数、微商,由速度变化问题和曲线的切线问题而抽象出来的数学概念.又称变化率.导数的发展大致经历了三个阶段:第一阶段:大约在1629年,求曲线上一点切线法的方法被法国数学家费马发现,后面他又研究出一个非常著名且重要的定理——费马定理.以此为基础,后来他又发现了求取极值的方法.1637年左右,他写一篇手稿《求最大值与最小值的方法》.在作切线时,他构造了差分f(A+E)-f(A),发现的因子E就是我们现在所说的导数f′(A).第二阶段:流数术的出现[2].17世纪,自然科学和生产力都取得了长足的进步,在原有科学技术发展和研究的基础上,数学家牛顿、笛卡儿、莱布尼茨等开始对微积分产生了浓厚的兴趣,开始深入研究微积分.“流数术”是牛顿研究出来的一种比较早的微积分基本理论,投用流量表示变量,他把流数称为变量的变化率,流数就相当于我们现在学习的导数,牛顿的主要成果有《求曲边形面积》《运用无穷多项方程的计算法》和《流数术和无穷级数》等.流数理论的实质概括为:他的重点在于一个变量的函数而不在于多变量的方程;在于自变量的变化与函数的变化的比的构成;最在于决定这个比当变化趋于零时的极限[3].第三阶段:逐渐成熟阶段.1750年,达朗贝尔在《百科全书》中提出了导数的概念,1823年,柯西定义了导数的定义.19世纪60年代以后,魏尔斯特拉斯创造了ε-δ语言,对微积分中出现的各种类型的极限重新进行标准定义,所有的这些理论基础,后来就出现了我们现在学习的导数的定义.
二、重要求导方法介绍
我们学习了导数的定义,求导公式,导数四则运算,高阶导数以及隐函数求导等内容,其中关于求导方法,我们学习过.
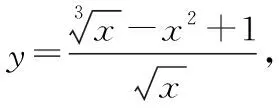
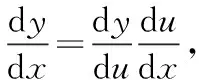

4.反函数求导法,反函数是我们熟悉的一类函数,但是我们仅仅是会求反函数,在高等数学中我们会遇到求反函数导数的问题,遇到这类问题时,我们先解出原函数的反函数,然后利用隐函数求导的方法,也就是两边同时求导(把带y的函数看成复合函数,y为中间变量),然后整理求出y′.例如,求y=ax的导函数,先求出y=ax的反函数x=logay,然后两边对x求导,可解得y′=axlna.通过例子,大家更明确了求反函数导数的方法.
5.参数方程求导法,两个变量x和y都是关于某个参数的函数,然后x和y分别对参数求导,然后带入公式,即可得出y′.
例如,x=3sint+t2,y=2cost-1,求解y′时,先求得
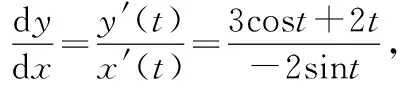
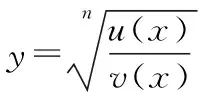
三、结 语
导数的学习是接下来学习积分学的基础知识,同时这部分知识也是整个高等数学课的重点也是难点.学好导数对于我们了解导数的背景,定义、几何意义等有很重要的现实意义,例如,我们可以利用导数求函数单调区间和极值、凹凸区间、拐点以及切线方程和法线方程,还有就是可以求函数微分、函数和实际问题的近似计算以及一些函数的极限问题、甚至求函数曲率都必须运用导数知识求解,以及最大值和最小值,包括函数在实际问题中的最值.通过本文,我们对导数的基本知识和求导方法有了更加深刻的认识,对于导数重难点也有了更深刻的认识.本文介绍了导数的起源,让读者对导数有了更深的认识,后来又简单介绍了几种常用和重要的求导方法,并简单进行了分析说明,特别是对对数求导法着重进行了着重阐述,因为对数求导法的基础知识为复合函数求导,因此,在分析对数求导法时,先简单介绍了复合函数求导,.对于对数求导方法我们先给出常见类型并且后又给出典型例题,特别对于对数求导的做题步骤进行详尽描述.对于几种求导方法,相信读者已经有了非常深刻的认识,对于读者熟悉掌握导数这部分知识有非常重要的意义.
