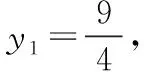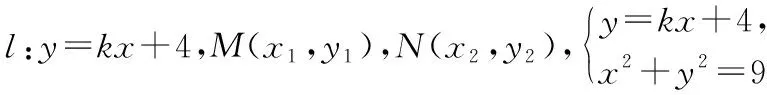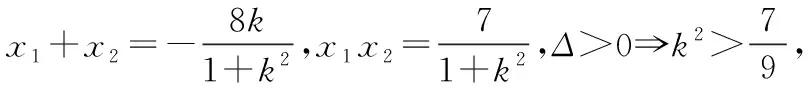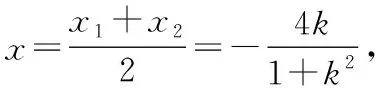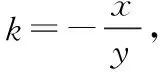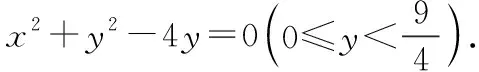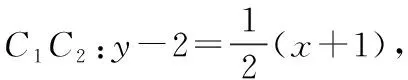“直线与圆的位置关系”的教学思考

◎苏仕刚

(安徽省肥东第一中学，安徽　合肥　231600)

由平面几何知识可知，直线与圆有三种位置关系：(1)直线与圆相交，有两个公共点；(2)直线与圆相切，只有一个公共点；(3)直线与圆相离，没有公共点.判断直线与圆的位置关系的方法有：一种是几何观点，即通过计算圆心到直线的距离d与半径r的大小来判断，若d>r，则相离；若d=r，则相切；若d

淡化方程观点的方法，这与教材的精神也不符.教材在内容的设置上也体现出要我们认真对待用方程的观点来研究这部分相关内容的，如，人教版必修2的137页，首先就用这样的思考：“现在如何用直线的方程与圆的方程判断它们之间的位置关系？”来引入用方程的观点来探究直线与圆之间的位置关系，也容易让学生在回顾第三章已经运用直线的方程研究了直线之间的位置关系，以及直线与直线间位置关系的简单运用，很快就过渡到本节也可以采用这种方法来研究直线与圆的位置关系及其相关的一些问题，从而把这种方法推广为一种研究直线与曲线之间关系的通法.此外教材在本节138页的例1给出了两种解法，首先就给出了从直线与圆的方程出发，通过它们的方程组成的方程组的实数解的情况，来判断直线与圆之间的位置关系，并把这种解法作为该例题的方法一，从而也突出了这种思维方法的重要性，所以我们在教学的过程中理应重视它.

也有的观点认为在这里运用方程的观点来联立方程组，有时方程处理起来又非常麻烦，浪费了教学时间，不如用几何的观点简单快捷，学生易操作.特别是高中数学课堂教学时教师们普遍感到平时教学的时间很紧，在这里再来花时间强调乃至拓展强化这种方程的观点，总觉得有点不值.这种观点我认为是教学目光短浅的一种表现，若把它放到整个教学体系上去看待本节知识，认识这种方程的观点，在这里花点时间来帮助学生对这种解题理念的形成，你就会觉得很值很有必要了.在解析几何中，直线与圆的位置关系是很重要的一个知识，不仅可以对学生的数学思维有一个很好的锻炼和提升，还将“曲线与方程联系起来，实现形与数的统一”的这种重要的解析几何的数学思想传输给学生，也为学生后续学习直线与圆锥曲线的位置关系奠定良好的基础.所以除了讲好教材中直接体现这种方程观点的知识内容外，还应引入一些问题来帮助学生形成这种数学思想，并会用这种思想方法来独立地分析问题解决问题.

问题一已知圆O的方程：x2+y2=9，求过点A(0，4)所作的圆的弦中点P的轨迹方程？

方法一如图所示，设弦MN中点P(x，y)，

⟹x2+y(y-4)=0⟹x2+y2-4y=0.

⊗

以方程⊗的解为坐标的点都在弦中点P的轨迹上吗？∵A点在圆外，∴过A点所作的直线与圆O不一定相交，故只能是方程⊗的部分解为坐标的点所对应的轨迹.现在过A点作圆O的切线，切点分别是D，E，并设D(x1，y1)，E(x2，y2)，∴直线AD的方程：xx1+yy1=r2=9.

①

②

问题二已知直线l：2x+y+4=0，圆C1：x2+y2-4y+2x+1=0.当l与圆C1交于A，B两点，求过A，B的圆C2的面积最小时圆C2的方程.

分析以|AB|为直径的圆的面积最小.

方法二以AB为直径的圆方程

(x-x1)(x-x2)+(y-y1)(y-y2)=0

⟹x2+y2-(x1+x2)x+x1x2-(y1+y2)y+y1y2=0.

⊗

其中y1y2=4x1x2+8(x1+x2)+16，

y1+y2=-2(x1+x2)-8.

代入方程⊗可得圆C2的方程：

方法三设x2+y2-4y+2x+1+λ(2x+y+4)=0

∵C2在直线l上，

方法四∵AB是圆C1的弦，且C2是AB的中点，

∴直线C1C2垂直平分AB，

通过上述问题的引入与讲解，不仅能引导学生在学习解析几何时要有“方程观点”的意识，还能让学生初步形成用代数的方法解决解析几何问题的能力，也为将来学生进一步学习选修1-1、选修2-1中的“圆锥曲线与方程”打下坚实的数学基础.

所谓“方程的观点”就是解析几何中坐标法这一重要数学思想的体现.我们在平面解析几何初步的教学中，一定要让学生真正地经历这样的学习过程：通过建立平面直角坐标系，将所研究的几何问题代数化，用代数的语言描述几何要素及其关系，即建立曲线与方程的等价性.再通过处理代数问题，分析代数结果的几何意义，最终解决几何问题.这种教学思想理念应贯穿平面解析几何的教学始终，一定不能偏离这个主线，否则对学生数学能力(数形结合的思想方法)的形成就会产生很不利的影响.