浅谈高中数学解题中的数学思维之美

◎沈东芸

(佛山科学技术学院数学与大数据学院，广东　佛山　528000)

通常大部分人一提到数学美，都会涉及简洁美、对称美、和谐美、奇异美等，这些都属于利用数学知识所创造出来的外在美.而数学是思维的体操，数学思维是真正的数学学习的充分条件.笔者认为数学美不仅仅只体现外在美，还体现内在美——数学思维之美，这里将从数学解题中来探讨解题思维，欣赏数学思维之美.

一、数学思维之美的体现

数学思维美[1]是数学学习中火热思考的过程，是波利亚所说的“解题过程中关键性步子”，是弗赖登塔尔所说的“再创造”，是涂荣豹教授所说的“数学本质”.因此，笔者认为数学思维之美主要体现在数学思维的深刻之美、转化之美、抽象之美.

二、数学思维的深刻之美

数学是深刻的，数学的深刻性使得数学分化出了不同的层次：整数比自然数更深刻，实数比整数更深刻，而复数比实数更深刻.越上层的数学能从更优的角度看待问题，越能解决底层轻易不能解决的问题.除了这些深刻的数学理论，数学思维的深刻性也值得强调，数学思维的深刻之美是值得数学爱好者欣赏的一种美.顾沛教授曾经也说，“数学的美，在于数学思想深刻之美”[2].欣赏数学思维的深刻之美要求我们对数学知识必须有深刻地理解和认识，也就是要求我们找到数学的本质，建立不同板块知识之间的联系或者同一知识的不同表现形式之间的关系.

例如，对直线与圆的位置关系，我们既可以利用圆心到直线的距离与半径的大小关系进行判断，又可以利用直线与圆的交点个数进行判断，这就将平面几何的知识与方程的知识建立联系.又如，对圆的方程(x-a)2+(y-b)2=R2，可以从两个方面来认识理解：一是从勾股定理角度出发，可将|x-a|，|x-b|看作是直角三角形的两直角边，R看作是直角三角形的斜边；二是从三角函数角度出发，因为sin2θ+cos2θ=1，可令(x-a)2=R2cos2θ，(y-b)2=R2sin2θ，从而将x,y用三角函数表示出来[1].像这样建立各个板块知识的联系会使很多问题得到简化，因此，在教学中要注意培养学生这方面的能力，引导学生深刻理解不同知识板块之间的关系，锻炼学生数学思维的深刻性，这样才能让学生体会这种深层次的美.

另外，数学思维的深刻之美还体现在数学解题过程中的另类思考方式和巧妙的处理方法.也就是说，对同一个问题，可能有多种解法，从不同的角度去看待，就会有不同的处理方法.如例1的第(2)小题：

例1设数列{an}的前n项和为Sn，满足2Sn=an+1-2n+1(n∈N*)，且a1,a2+5,a3成等差数列.

(1)求数列{an}的通项公式；

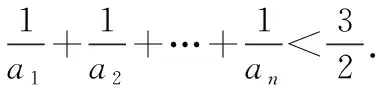
对第(2)小题，有4种解法，可以归结为三类：第一类是转化为等比数列求和；第二类是通过列项求和；第三类是利用构造函数证明不等式[3].对同一个问题，从不同角度出发呈现出不同的思考方式，体现了数学思维的深刻之美.

三、数学思维的转换之美

数学思维的转换蕴含在数学解题中，数学解题就是把未知的问题转化为已知的问题，把复杂的问题转化为简单的问题等等.在转化的过程中，不仅有利于实现学习知识的迁移，而且学生的数学思维也在转换，体现数学思维的转换之美.在教学中，引导学生从数学美的角度来促使数学问题的转化，同时培养学生欣赏数学思维的转换美，不仅有利于激发学生学习数学的兴趣，还有利于打造高效数学课堂.例如，函数、不等式、方程的综合问题既是高考的热点又是高考的难点，难点就是如何进行函数、方程、不等式的转化和利用.因此，在教学中应注意引导学生将方程、不等式问题转化为函数问题或者是将函数问题转化为方程问题等，只有学生明白“为什么要转化？”“怎么转化？”“何时转化合适？”这三个问题，才能体会数学思维的转换之美.如例2就是将方程问题转化为函数问题：

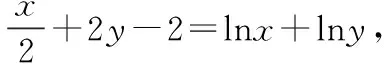
思路分析这是一个含有两个未知实数的方程，一般不能通过解方程得到，也就是说不能从“方程”这一角度解答，需进行转化，因此，考虑将方程问题转化为函数问题来解决.因为对于方程f(x)=c可以看成是函数y=f(x)中y=c时求x的值，也就是说解方程的过程实际上是求函数值的逆向问题.当c取若干个值时，x就是若干个y值所对应的所有x值，此时解方程就可以看成是已知函数值域求所有x的取值集合[4].

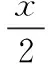
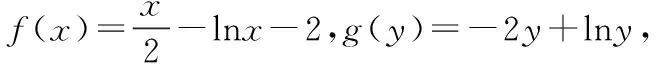
不妨设f(x)=g(y)=c，原方程的解即为两个函数函数值相等时所对应的所有自变量的取值.

本题通过问题转化，使原本无法解决的问题得以解决，数学美就是问题解答所带来的这种美感，数学思维的转换就是问题解答中的关键一步，因此，体现了数学思维的转换之美.

四、数学思维的抽象之美

抽象性是数学最大的特点，抽象就是舍去若干不同事物的不同点，得到它们的共同点.数学抽象是指舍去事物的一切物理属性，得到数学研究对象的思维过程.数学思维是数学学习活动的核心，数学抽象思维又是数学思维的核心.数学抽象思维[5]是指对数学对象，如空间形式、数量关系的本质属性和内部规律的一种间接的反映，然后按照一般的思维规律去认识数学内容的理性活动.心理学研究表明，高中学生已经能进行抽象思维，因此，在数学教学中，应注意培养学生领会数学思维的抽象之美，不仅有助于提高学生的解题能力，还可以提高学生学习数学的兴趣.

例如，例2的求解给予我们启发，将例2的解题思维进行抽象概括：对于能够分离的二元方程，可以转化为两个函数的函数值相等，再结合相应的函数性质(最值、单调性等)求解.

变式1已知函数f(x)=ex，g(x)=-x2+4x-3,若有f(a)=g(b)，求实数b的取值范围.

变式2已知函数f(x)=x·ex,x∈(-∞,2)，函数g(x)=ax+1,x∈[-2,2]，∀x1∈[-2,2]，总存在x0∈(-∞,2)，使得f(x0)=g(x1)成立，求实数a的取值范围.

变式1、变式2与例1都属于二元方程问题，本质上都是分离后可转化为两个函数值域的交集问题.学生掌握了将二元方程问题转化为两个函数值域关系来求解问题的思维，在今后的学习中，无论题目中的数学对象、数量关系怎么变化，只要本质上属于这一类问题就都可以用这种思维解决问题，这就是体现数学的抽象思维，这些成果进一步展现了数学思维的抽象之美.

五、数学思维之美在数学解题教学中的应用建议

思想无法替代，思维无法复制.教师在教学中应注意自己的角色定位，科学地把握学生的认知规律，科学地培养学生的数学思维，做一名科学的引导者.

(一)注重数学思想方法的渗透

在数学解题教学中，应注重数学思想的渗透，一是挖掘隐藏在题目中的数学思想方法；二是要将“方法”提升到“思想”，扩展学生的数学思维；三是注重引导学生将数学思想方法进行迁移、运用，要创设平台让数学思想方法与学生原有知识建立联系，培养学生分析、归纳探索的能力，这样才使问题有了思考的火花，才能引导学生一起领略数学思维之美.

(二)注重数学本质的理解

理解数学的本质，是数学学习的重中之重.在数学解题教学中，也要注重数学本质的理解，才能建立知识与知识之间的联系.只有学生从根本上掌握这些知识，才能在解题中进行问题的转化，体现数学思维之美.

(三)注重思维过程的暴露，进行思维的再创造

在解题教学中暴露数学的思维过程是非常重要的，不仅要暴露教师的数学思维过程，还要暴露学生的思维过程，让学生将自己的思维过程和教师的思维过程进行比较，从比较中去体会和领悟数学思维之美.然后可以对思维方法进行拓展，从不同的角度对现有的问题进行探究，培养学生的创新思维.