“心有灵犀一点通”“心有灵犀一点通”——浅谈高中数学解题中常用的四大数学思想

◎赵艳芳

(安徽省淮南第一中学，安徽　淮南　232001)

当前，很多高中生在解数学题时，思维非常机械，能动性低，缺乏数学思想与数学思维，虽然平时花了很多时间，但是由于效率过低，往往达不到预期的效果.究其原因，是因为这些高中生在解题时没有形成系统的数学思想，思维模式僵化，解题时思维过于狭窄，往往是为了做题而做题，不能触类旁通，举一反三.因此，在学习高中数学时，数学思想的灵活运用非常重要.高中数学教师在课堂教学时应注重培养学生的数学思想与数学思维.

一、数形结合思想

数学是非常重要的基础学科.数学的主要功能就是用来刻画我们现实生活中事物之间的数量关系以及空间分布形式，也就是所谓的“数”与“形”，而且“数”与“形”之间不是孤立的，而是相互联系，相辅相成，有密切的关系.在数学解题中，如果能够将“数”与“形”两者有效结合起来，往往可以让人眼前一亮，茅塞顿开，显著降低解题的难度，大大提高解题的效率.下面我们以例1简单地介绍一下数形结合思想的运用.

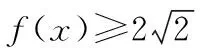
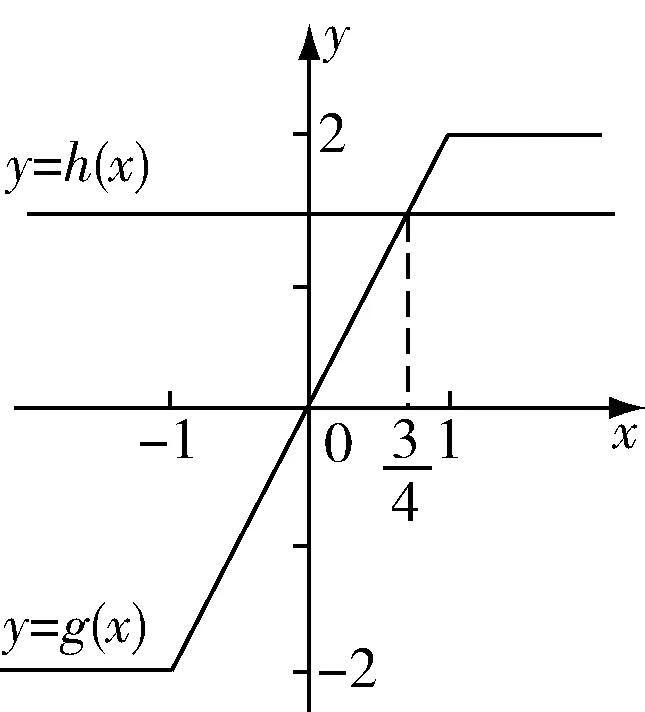
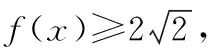
从例1的解题过程可以充分表明，数与形之间存在着密切的联系，很多代数问题若能转化成图形，则思路和方法可以从图形中直观地显示出来.通过观察数与形之间的关系，非常直观，一目了然，很快会找到解题方法.

二、函数与方程思想

跟数形结合思想一样，函数与方程思想也是高中数学解题中的一大重要数学思想，这种思想在历年的高考试题中也都有体现.这种思想的精髓在于，利用函数分析数学中的数量关系，结合函数的图像与性质去分析解决问题；再通过构造方程，运用方程的性质转化问题，分析问题，最终解决问题，体现了函数思想与方程的思想的珠联璧合，展现了函数与方程之间的密切关系.在高中数学解题中，有很多函数问题可以通过转化为方程来求解，而很多方程问题同样也可以通过转化为函数来求解.下面的例子就体现了这种思想.

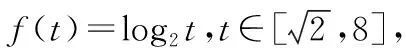
原题转化为：m(x-2)+(x-2)2>0恒成立，为m的一次函数(这里思维的转化很重要).

当x=2时，不等式不成立.

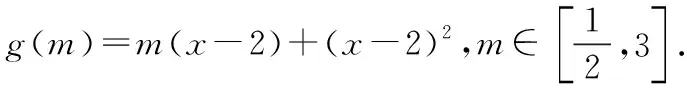
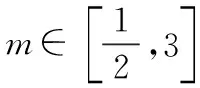
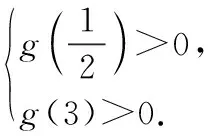
函数与方程思想利用函数、方程的观点和方法处理变量或未知数之间的关系，从而获得解题方法的一种思维方式，是一种很重要的数学思想.利用该思想来解决一些比较复杂的问题时，往往会使人有一种“拨开云雾见太阳”的感觉，事半功倍.

三、分类讨论思想

分类讨论的思想在高中数学解题中也得到了广泛的运用，它指的是在解题时必须要考虑到研究对象的性质差异，要根据不同的情况将研究对象分类分析，从而最终解决问题.分类讨论思想根据数学研究对象的“物以类聚”这一特点，在解题时，要依据数学研究对象本质属性的相同点和差异点，将数学对象划分为不同种类分别进行研究和求解，本质上是一种化整为零、化繁为简、分别对待、各个击破的思维策略在数学解题中的应用.

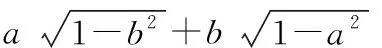
解析∵a2+b2=1，∴a2=1-b2，b2=1-a2.

∵ab>0，∴a>0，b>0或a<0，b<0.

(1)当a>0，b>0时，

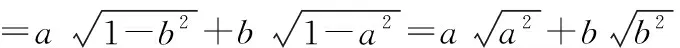
=a|a|+b|b|=a2+b2=1.

(2)当a<0，b<0时，

原式=a|a|+b|b|=-a2-b2=-1.

即原式的值为1或-1.

从上面的例题我们可以看到，分类讨论思想根据数学研究对象的性质差异，分各种不同的情况来分析解决问题，具有较强的逻辑性和很强的综合性，所以，在使用分类讨论思想解题的时候，应该注重理解和掌握分类的原则、方法和技巧，力求做到“确定对象的全体，明确分类的标准，分层别类不重复、不遗漏的分析讨论.”

以上三种数学思想可以说是高中数学解题中的最重要的几种思想.教师应该加强渗透这几种数学思想的教学，指导学生对这些进行反复的学习、思考、领悟.数学思想把千丝万缕的数学知识编织在一起，真正领悟这些数学思想也需要一个过程，在此期间教师应该积极的引导学生，培养学生的创造性思维，避免学生机械的模仿和生搬硬套，应该鼓励学生能动的、创造性的进行学习，领悟数学思想的精髓，在解题时真正能够达到“心有灵犀一点通”.