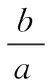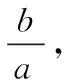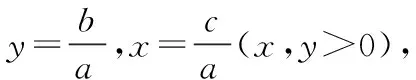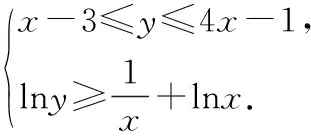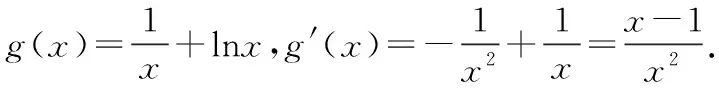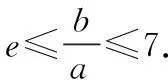授学生以渔,从教他们“如何理解题意”开始
2018-07-17朱丽娟
◎朱丽娟
(江苏省扬州大学附属中学东部分校,江苏 扬州 225002)
波利亚在他的《怎样解题》中给出了一张解题表.他的解题过程的第一步就是弄清问题,即清楚地了解问题,弄清它的主要部分.涂荣豹老师在他的《论反思性数学学习》中指出:“就学习解题而言,最重要的是‘理解题意’和‘解题回顾’,因为这是最终学会‘制订解题计划’的前提和基础.”数学教学离不开解题教学,而解题首先要重视的问题就是引导学生迈出解题的第一步——审题,即理解题意.
以信息论的观点看,就是如何获取信息和如何加工信息.事实上,中学生获取信息很容易,因为多年来,学生的解题经验已经让他们懂得,数学题中没有多余的信息.然而,如何加工信息才是关键.在阅读题意的过程中,如何将获取的信息快速准确地翻译为自己的语言,这中间还有一个判断的过程,考查的是什么知识点?这个知识点是定义还是公式或是具体的操作方法?要注意的是什么?若干个知识点之间的关联是什么?已知量和未知量之间的桥梁信息又是什么?
学生在进行数学解题时,指导他们解题前审题要慢,读懂题意并且给出判断;判断涉及哪些知识点,这些知识点的考点和主要点在哪里;动笔时,计划怎么做,思路是否畅通可行.
下面从三个方面来看,高三复习中的审题指导和训练.
一、注意题目条件之间的实质关系
2012江苏卷12题:在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是________.
分析这个题目,不少学生首先想到的是先将圆的方程表达出来,利用圆和圆的位置关系来进行求解.
解法1设存在直线y=kx-2上一点的坐标P(x,kx-1),使得以P为圆心,半径为1的圆与圆C有公共点,
故|rP-rC|≤CP≤rP+rC,
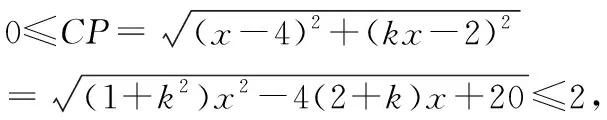
即不等式(1+k2)x2-4(2+k)x+16≤0有解.
所以,Δ=[4(2+k)]2-4(1+k2)·16≥0,
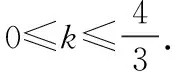
评析这是按照题目给出的条件,先设出圆的方程,再利用圆和圆的位置关系构造含有k的不等式,进行求解,这是直线型的思考方式.如果我们读题后做进一步的思考,就会发现,点是直线上的动点,而直线可以看成是过定点(0,-2)的除垂直于x轴的直线系,圆C是已知圆心和半径的定圆.这就使得我们不妨从直线和圆的位置关系的角度来进行研究,即利用圆心到直线的距离这个量来进行刻画.容易发现,圆C的圆心到直线的距离d≤2.
于是,解法2如下:
因为直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
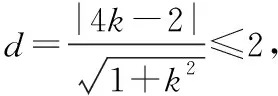
二、注意题目中隐含条件的挖掘
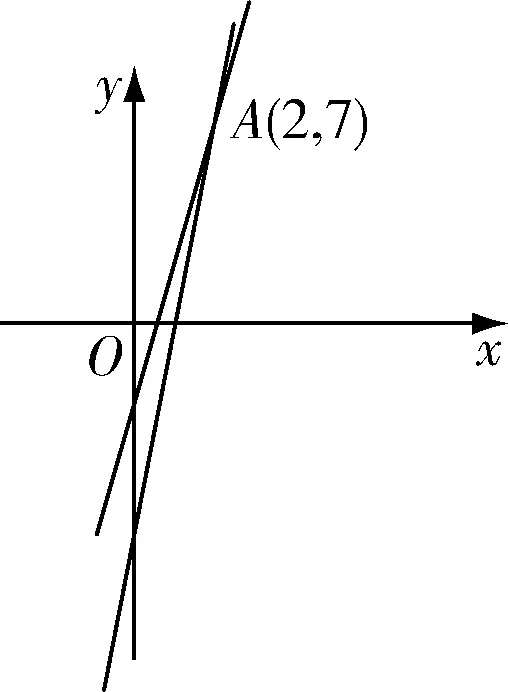
2012江苏高考13题:已知函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞),若关于x的不等式f(x) 但是,仔细挖掘题目的隐含条件就会发现,如图所示,由函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞)可得, Δ=a2-4b=0. (1) 又方程f(x)=c的两根之差的绝对值等于6,则 (2) 由(1)(2)可以很快解得,c=9. (1) (2) 由(1)得,y≤7. 当x=1时,g(x)min=g(1)=1,故lny≥1,y≥e.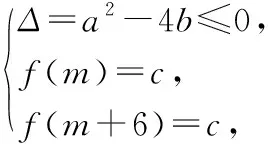
三、注意树立合理的目标意识