例谈高中数学教材习题的自学指导策略
2018-07-17唐海军
◎唐海军
(四川文理学院数学学院,四川 达州 635000)
在数学课堂中,习题常常被误以为只是理解新知识的巩固性、一次性材料.在学生纠错之后,一道道习题便完成了使命,至于习题的“评价作用、总结作用、教育作用、文化熏陶”[1]等功能全然没有发挥出来.陈希孺院士曾经说:“学好数学重在多做习题.”[2]习题也应该是一种地位等同于教材正文一般重要的学习材料.习题也需要学生课前自主预习,课后巩固复习.下面通过“圆锥曲线与方程”一章几个例题来说明学生在自学教材习题时,应该多注意所学知识之间的联系,最终达到自学教材,解决习题的目的.
一、由命题推导中获得的结论解决习题问题
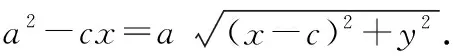
①
若对该等式进行不同的等价变形,可得到不同的结论.
对①式,人教版教材的处理方法是:上式两边再平方,整理,并令a2-c2=b2(b>0),就得到了焦点在x轴上的椭圆的标准方程.
人民教育出版社普通高中课程标准实验教科书A版(简称“课标版”,下同)数学选修2-1上的这种两次平方法推导,在19世纪以前没有一位数学家采用,直至英国数学家萨尔蒙(1819—1904)在1855年才开始使用.随后英国数学家卡西(1820—1891)、美国数学家纽库姆(1835—1909)相继采用.而到了20世纪,在各国应用椭圆第一定义的教材中,推导时几乎都用了此法.究其原因,两次平方法虽然比较繁复,但却具有通性通法,即介绍了如何化简含有两个根式的一般方法.正是基于这样的优点,我国教材也一直采用该法.[3]
对①式处理方法二:两边同除以a,有
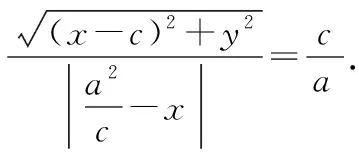
②
这自然获得了椭圆的第二定义.
例1(课标版选修2-1,第二章圆锥曲线的复习参考题B组-3题)点M与定点F(2,0)的距离和它到直线x=8的距离的比是1∶2,求点M的轨迹.
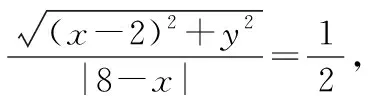
二、由例题研究到习题自学
教材例题是教材的重要组成部分,一般具有典型方法的示范性.“例题或寓有一般结论,或者蕴含深刻的背景材料.”[4]学生对习题的自学可以尝试从例题与习题的联系入手.
例2(课标版选修2-1,2.4节例4)斜率为1的直线经过抛物线y2=4x的焦点,与抛物线相交于两点A,B,求线段AB的长度.
解易知抛物线焦点F的坐标为(1,0),直线AB的方程为y=x-1,将其代入抛物线方程y2=4x中,得x2-6x+1=0.从而xA+xB=6.
再由|AB|=|x1+x2+p|,得线段AB的长度为8.
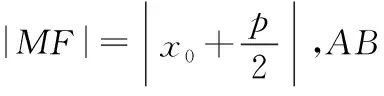
例3(课标版选修2-1,习题2.4,A组-5题)M是抛物线y2=4x上一点,F是抛物线的焦点,以Fx为始边、FM为终边的角∠xFM=60°,求|MF|.
三、由教材探究例到习题自学
为体现课标关于学生自主探究学习的理念,教材编写中设置了相当数量、主题丰富的探究式栏目.对这些探究题的学习,有利于拓展知识面与知识结构的完善.
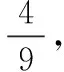
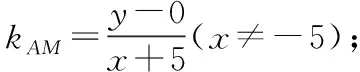
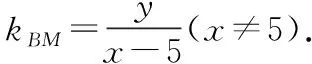
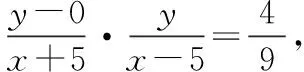
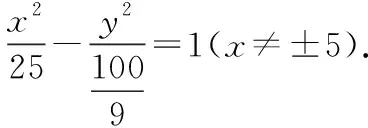
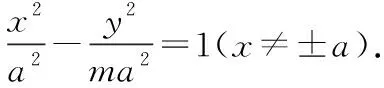
当m>0时,M轨迹为双曲线;当m<0且m≠-1时,M轨迹为椭圆;当m=-1时,M轨迹为圆.从而得出:平面内与两定点的连线的斜率之积是常数k的动点的轨迹也可能是椭圆.[5]此结论,可用来解决习题,如课标版选修2-1中的第二章圆锥曲线的复习参考题A组-10题:已知△ABC的两个顶点A,B的坐标分别是(-5,0),(5,0),且AC,BC所在直线的斜率之积等于m,试探求顶点C的轨迹.
四、由练习题目类比解决新习题
郑毓信教授认为数学基础知识,不能理解成各个孤立的知识点,简单言之,对基础知识“不应求全,而应求联”.为了帮助学生很好地掌握数学基本技能,数学的解题“不应求全,而应求变”.[6]数学教师在布置习题时,不应满足于简单的重复,而应帮助学生学会在各种变化的条件下对各个基本技能的辨认和应用.
对①式处理方法三:两边同除以a,有
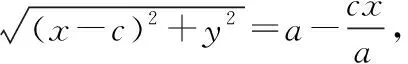
当c>0,则|MF2|=a-ex;当c<0,则|MF1|=a+ex.称它们为椭圆的焦半径公式.
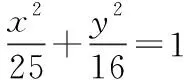
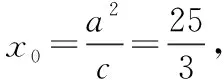
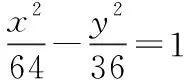
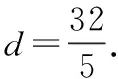
常言道:“授之以鱼,不如授之以渔.”数学的学习原理与此相同.习题解答如果仅仅停留在一题一练,也只是满足各个知识点的释义,个别方法的应用,至多算是“授之以渔具”.习题课的教学要“充分发挥教材习题的优势,加强习题联系,重视变式训练”[7].指引学生自学习题,要从寻找习题与数学定义、习题与例题、习题与探究、习题与习题等方面的联系入手来探寻“捕鱼之道”,从而逐步增强高中生自主学习与探究学习的能力,达到高中数学课程标准对中学生数学学习的要求,实现举一反三、触类旁通的效果.
