换元法思想在数学学习中的几种常见应用

◎姜春阳

(滁州二中，安徽　滁州　239000)

换元法又称辅助元素法、变量代换法.通过引进新的变量，可以把分散的条件联系起来，隐含的条件显露出来，或者把条件与结论联系起来，或者变为熟悉的形式，把复杂的计算和推证简单化.它可以化高次为低次、化分式为整式、化无理式为有理式、化超越式为代数式，在研究方程、不等式、函数、三角、数列等问题中有广泛的应用.

一、换元法在求解函数解析式上的应用

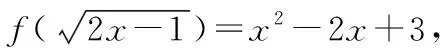
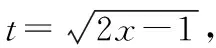
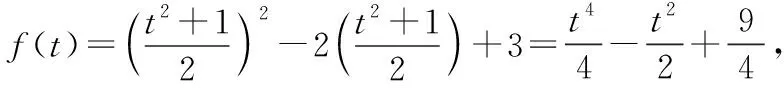
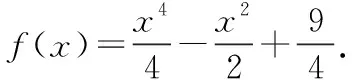
二、换元法在求解函数值域上的应用

(一)换元法在求解指数型函数值域上的应用

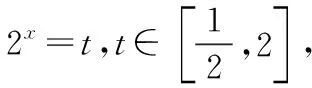
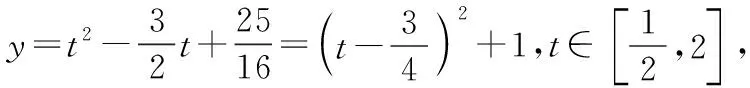
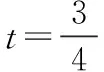
(二)换元法在求解对数型函数值域上的应用

例3已知函数f(x)=ln2x-2lnx+3，x∈[1，e3]，求函数f(x)的值域.

解令t=lnx，则t∈[0，3]，

故y=t2-2t+3=(t-1)2+2，t∈[0，3].

当t=1时，ymin=2；当t=3时，ymax=6.

故函数f(x)的值域为[2，6].

(三)换元法在求解三角函数值域上的应用

例4已知函数f(x)=cos2x+2sinx-1，求函数f(x)的值域.

解f(x)=cos2x+2sinx-1=1-sin2x+2sinx-1=-(sinx-1)2+1.

令t=sinx，则t∈[-1，1]，

所以当t=1时，ymax=1；当t=-1时，ymin=-3.

(四)换元法在求解无理根式值域上的应用

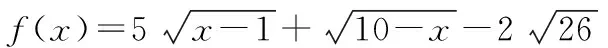
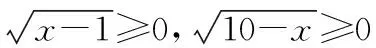
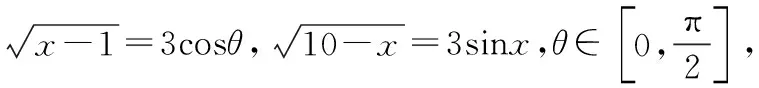
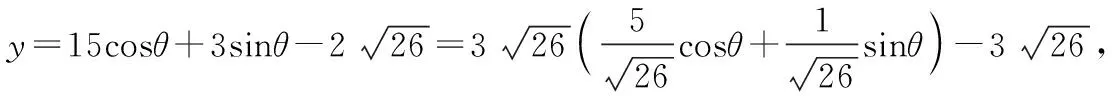
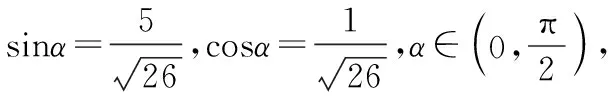
∵θ+α∈(0，π)，∴(sin(θ+α))max=1，

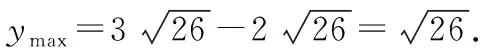
三、换元法在求解函数单调性上的应用

例6已知函数y=ln(x2-2x+3)，求此函数的单调递减区间.

解令y=lnu，u=x2-2x+3=(x-1)2+2.

∵y=lnu单调递增，而u=(x-1)2+2在(-∞，1]上单调递减，

故复合函数y=ln(x2-2x+3)在(-∞，1]上单调递减.

四、换元法在求解函数奇偶性上的应用

例7已知f(-x-2)=f(x+2)，试判断函数y=f(x)的奇偶性.

解令t=x+2，则有f(-t)=f(t)成立，故y=f(x)为偶函数.

练习：已知f(1-x)=-f(x-1)，试判断函数y=f(x)的奇偶性.(奇函数)

五、换元法在求解函数周期性上的应用

例8已知函数y=f(x)满足f(x+1)=-f(x)，求函数的周期.

解令t=x+1，则x=t-1，故等式可变形为f(t)=-f(t-1)，即-f(t)=f(t-1)，

∴-f(x)=f(x-1)，

(1)

f(x+1)=-f(x).

(2)

联立(1)(2)可得f(x+1)=f(x-1)，再令t=x-1，则此式可变形为f(t+2)=f(t)，故函数y=f(x)的周期为T=2.

可见，换元法对于研究函数的性质有着广泛应用，在教学中应当把换元法思想作为一种重要的解题思想传授给学生，这样对于学生在学习函数的时候帮助会很大.